
L'âge de son logarithme
« Hâtons-nous : le temps fuit, et nous traîne avec soi. »
Ce vers de Nicolas Boileau (1636-1711) reflète un sentiment de rétrécissement du temps, souvent ressenti à la maturité. Au contraire, les enfants ont plutôt l'impression que le temps n'en finit pas. Le regretté généticien Albert Jacquard (1925-2013) a vu une relation mathématique derrière ce sentiment. Nous ressentirions non pas notre âge mais son logarithme, en comptant la naissance à la conception. Pour un enfant né à terme, en comptant son âge x en années, ce serait log(x + 3/4). Son aventure commencerait donc à trois mois, où le ressenti de l'âge serait nul. On arriverait à 1 à l'âge de 9 ans et 3 mois, et à 2 à près de 100 ans.
Si on comprend l'ajustement du début de la vie à la conception afin de faire coïncider l'âge nul à la naissance, il semble exagéré de penser qu'on ressente une même durée entre les dix premières années et les quatre-vingt-dix suivantes. Mais l'idée d'Albert Jacquard réside dans le fait qu'à chaque instant, on estime le temps passé relativement à la part de sa vie déjà vécue. Ainsi, 5 ans à 50 ans sont 10 % de votre vie, alors que 10 % de votre vie à 10 ans est seulement 1 an.
Loi de Benford et tables de logarithmes
En 1881, dans l'American Journal of Mathematics, Simon Newcomb, mathématicien et astronome, constate que les premières pages des tables de logarithmes sont plus usées et noircies que les autres. Il note de même que, dans les suites de nombres prises dans un ensemble de données, la fréquence du chiffre 1 est plus grande.
Indépendamment, en 1938, le physicien Frank Benford remarque également l'usure inégale des tables de logarithme et en déduit une loi qui portera son nom : la probabilité de trouver un des chiffres de 1 à 9, à gauche d'un nombre, n'est pas la même pour tous les chiffres ! Cette probabilité qu'un chiffre n soit le premier chiffre d'un nombre est égale à log10(1 + 1/n).
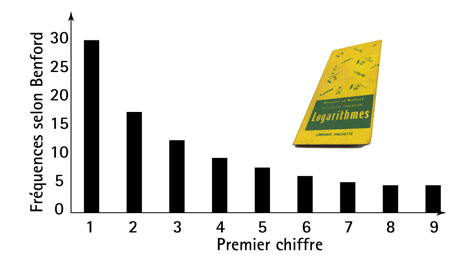
La loi de Benford s'applique aux nombres indiqués sur la première page d'un journal, à la population des villes, à la longueur des rivières ou à la durée de « demi-vie » des noyaux radioactifs. Elle est utilisée par les agents du fisc pour dépister des tricheries : les chiffres choisis dans les déclarations frauduleuses n'obéissent pas à la loi de Benford car ils ont été pris au hasard, donc avec d'égales probabilités. Comme quoi les hypothèses apparemment les plus « évidentes » ne le sont pas : vous commencez à calculer par le chiffre 1 et il n'est pas anormal qu'il apparaisse plus souvent que les autres (la cardinalité et l'ordinalité sont des propriétés différentes des entiers).
Il fallait un logarithme pour expliquer l'usure des tables de logarithme…
Lire la suite gratuitement