L'application inverse de l'exponentielle

Le propre des logarithmes est de transformer les multiplications en additions, opérations bien plus aisées à effectuer. Par là même, ils transforment les divisions en soustractions et les exponentiations en multiplications. Or, une exponentielle réalise le contraire. Pour définir un logarithme, une idée simple consiste donc à inverser une exponentielle. Voyons la méthode avec celle de base 10. Par définition, log x est le nombre y tel que x = 10^y.
Ainsi, log 1 = 0, log 10 = 1, log 100 = 2, etc. Voici un petit extrait d'une table de logarithme de base 10 :

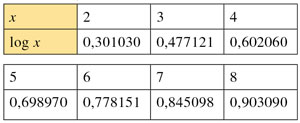
On peut y vérifier que log 4 = 2 log 2 et log 6 = log 2 + log 3. De façon générale, pour calculer le produit de deux nombres, disons 12,132 et 5,456, on cherche leurs logarithmes dans la table, ce qui donne ici log(12,132) = 1,083932402 et log(5,456) = 0,7368743616. On additionne ensuite ces deux nombres, ce qui donne le logarithme du produit P : log P = 1,820806764. En lisant la table à l'envers, nous obtenons alors P comme l'exponentielle de base 10 de ce dernier nombre, d'où P = 66,19219211, ce qui donne le résultat exact du calcul demandé en tronquant les deux dernières décimales.

Ainsi, l'utilisation des tables de logarithmes nécessite de la dextérité et de ne pas se tromper dans les additions. La précision de ces tables commande celle de tous les calculs, en particulier ceux qu'effectuaient autrefois les marins pour calculer le cap à maintenir. Une erreur pouvait causer un naufrage, ce qui fut d'ailleurs plusieurs fois le cas. En effet, construites à la main, les tables de logarithmes contenaient un grand nombre d'erreurs. C'est pourquoi Charles Babbage (1791-1871) voulut fabriquer une machine pour les établir. Les premiers ordinateurs servirent d'ailleurs à cela…

Le logarithme népérien

Toute fonction logarithme transforme multiplications en additions. En considérant la fonction exponentielle classique, dont la base est e = 2,718…, on obtient le logarithme népérien. À chaque valeur y > 0, il correspond une valeur x unique telle que y = e^x. Cette valeur x est le logarithme népérien de y, soit x = ln y. Les graphes des fonctions exponentielles et logarithmes sont symétriques par rapport à la première bissectrice D (d'équation y = x).

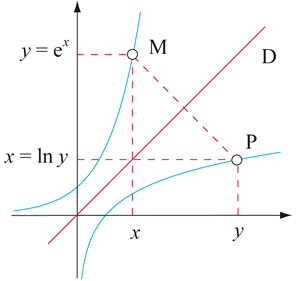
Même si on peut étendre l'exponentielle au corps des nombres complexes, on ne peut pas pour autant y étendre le logarithme car, d'après l'identité d'Euler,  \( e^{2i\pi}=(e^{i\pi})^2=(-1)^2=1,\) donc l'égalité y = e^x ne définit jamais x de façon unique sur le corps de nombres complexes. 

Plus précisément, si x vérifie cette égalité, tous les nombres x + 2 ik \( \pi\)  (où k est un nombre entier) la vérifient aussi. On peut alors définir un logarithme complexe à condition de se placer, par exemple, sur le plan privé du demi-axe des abscisses négatives.

De façon générale, les fonctions logarithmes sont les fonctions  f « suffisamment régulières » vérifiant f (x y) = f (x) + f (y) pour tout couple de nombres strictement positifs x et y. Il suffit de considérer les fonctions  f continues et non nulles, mais il est plus simple ici de s'intéresser aux fonctions dérivables non nulles (voir l'article Un logarithme sous l'hyperbole).

En effet, en dérivant l'égalité f (x y) = f (x) + f (y) par rapport à x (y est alors fixé), on obtient y f '(xy) = f '(x), d'où, en posant y = 1 / x, f '(x) = f  (1) / x, ce qui correspond à une hyperbole. En intégrant entre 1 et x, on obtient f(x) = f(1) + f '(1) ln x.

En portant x = y = 1 dans l'équation fonctionnelle, on obtient f(1) = 0, d'où f(x) = f '(1) ln x.
En posant a = exp[1 / f '(1)], on peut écrire f(x) = log_a x. 

Une autre façon d'opérer est de ramener l'équation fonctionnelle des logarithmes à l'équation de Cauchy, qui consiste à chercher les fonctions g vérifiant g(x + y) = g(x) + g(y) pour tout couple de nombres x et y. Pour cela, on pose g(x) = f(e ^x).
Si f vérifie f(xy) = f(x) + f(y), alors g vérifie l'équation de Cauchy, et réciproquement. Si f est supposée dérivable, alors g l'est aussi et, en dérivant par rapport à x, cette équation donne la relation g'(x + y) = g'(x), donc que g' est constante, ce qui mène aux fonctions linéaires, c'est-à-dire de la forme g(x) = a x. On retrouve le même résultat pour  f. On le trouve également en supposant seulement la continuité de la fonction, et même sa continuité en un seul point (voir l'encadré) ! Cependant, il existe des solutions discontinues en tout point ; il est hélas impossible de les expliciter.

Quand les logarithmes se font discrets

La notion de logarithme se généralise à un autre cadre, celui des groupes cycliques finis, comme par exemple l'ensemble des entiers {1, 2, 3, 4, 5, 6}, noté (ℤ / 7ℤ)*, muni de la multiplication modulo 7, c'est-à-dire que le produit de deux nombres est réduit à son reste dans la division par 7. Sa table de Pythagore est :

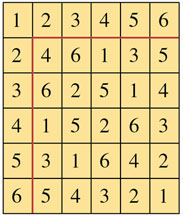
On dit que (ℤ / 7ℤ)* est cyclique car il est constitué par l'ensemble des puissances de certains éléments, comme 3 et 5 (mais pas des autres). En effet, l'ensemble des éléments de (ℤ / 7ℤ)* est 3⁰ = 1, 3¹ = 3, 3² = 2, 3³ = 6, 3⁴ = 4, 3⁵ = 5. Tous les éléments sont atteints !

Sur (ℤ / 7ℤ)*, on peut ainsi définir le logarithme de base 3 (et également de base 5), exactement comme dans l'ensemble des nombres strictement positifs : log₃ x est l'élément a du groupe tel que x = 3^a. Il n'est pas immédiat à trouver puisqu'il suppose d'inverser la fonction exponentielle. Voici la table de cette fonction :

On parle de logarithme discret (par opposition au logarithme continu) car le groupe est fini, donc discret. Ce problème du logarithme discret, difficile à résoudre dans des groupes de la forme (ℤ / pℤ)* quand p est un grand nombre premier, est à la base de plusieurs systèmes cryptographiques asymétriques, c'est-à-dire où savoir chiffrer n'implique pas que l'on sache déchiffrer.