Vous savez tous ce qu'est la médiatrice : il s'agit de l'ensemble des points équidistants de deux points donnés. On peut aller plus loin et envisager aussi des ensembles de points équidistants non plus de points isolés, mais d'autres ensembles de points. Puis, généralisant la notion, nous pouvons nous poser ces questions : quel est l'ensemble des points équidistants d'un point et d'une droite ? d'un point et d'un cercle ? d'une droite et d'un cercle ? Plus savant encore, nous pourrons imaginer l'ensemble des points équidistants de deux cercles ou encore – soyons fous ! – d'une droite et d'un carré. Autant de lieux géométriques à établir avant de les parcourir !

Des points, des droites et des cercles 

La première des équidistantes est le cercle : c'est l'ensemble des points équidistants de son centre. Très simple aussi comme exemple est la bissectrice d'un couple de droites sécantes : elle n'est rien d'autre que l'ensemble des points équidistants de deux droites.

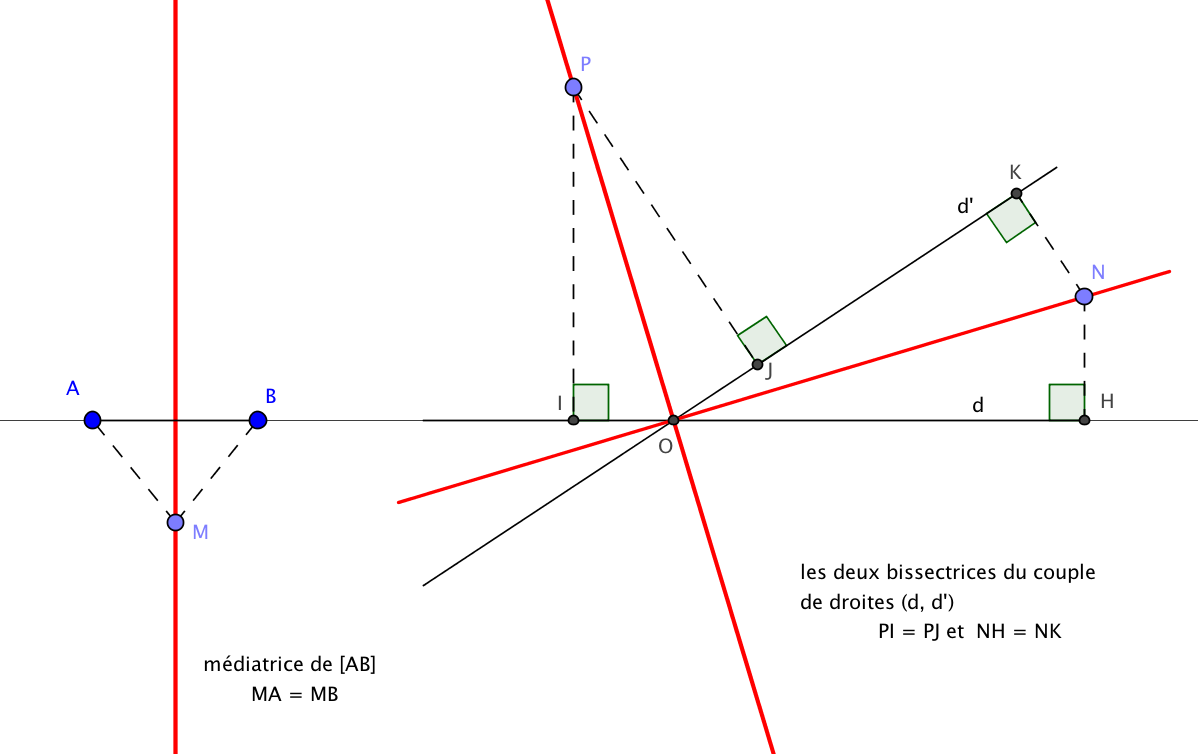
  Médiatrice et bissectrices.

Un autre exemple classique est celui de l'ensemble des points M équidistants d'un point F et d'une droite d donnés : voilà une « équidistante » simple, qui est la parabole de foyer F et de directrice d, ensemble des points M tels que MF = MH, si H est le projeté orthogonal de M sur la droite d (donc le point qui matérialise la distance de M à cette droite).

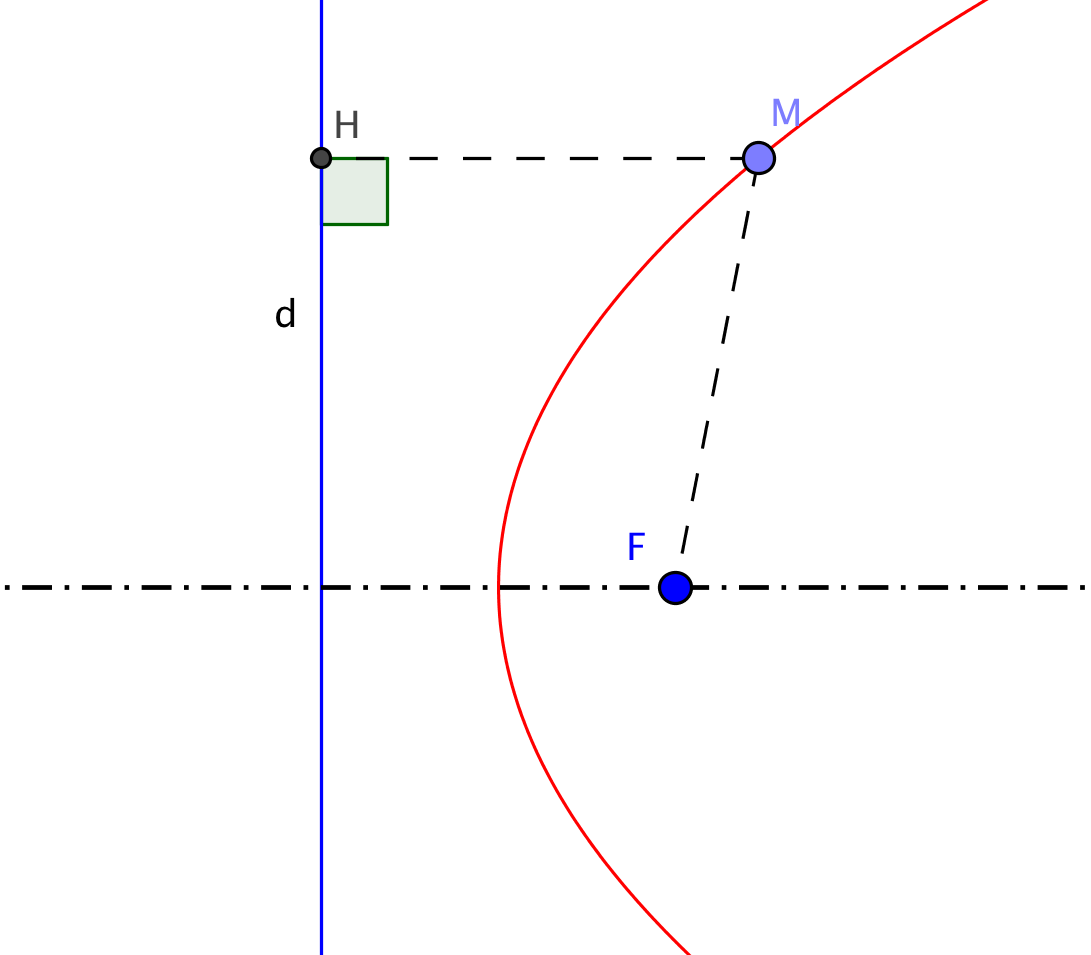
Parabole de foyer F et de directrice d.

Dotée de propriétés évidentes de symétrie autour de son axe focal, perpendiculaire à d issue de F, elle est très utilisée, non seulement en géométrie, mais en optique dans tous les phénomènes concernant la réflexion de faisceaux lumineux : en effet, tout rayon incident est réfléchi en passant par le foyer. On la rencontre d'ailleurs souvent dans les recherches d'équidistantes.

Si l'on sait bien ce que représente la distance d'un point M à un autre point ou d'un point à une droite, on sait moins ce qu'est celle d'un point à un autre ensemble (E) de points. On définit la distance du point M à l'ensemble (E) comme étant la plus petite distance de M à P, P étant un point parcourant l'ensemble (E). Par exemple, la distance du point M au cercle (C) de centre F et de rayon r est égale à la distance MP, P étant le point du cercle (C) « le plus proche » de M. Cela signifie concrètement que MP = | MF – r |.

  p.p1 {margin: 0.0px 0.0px 0.0px 0.0px; text-align: center; font: 9.0px 'Block Berthold Condensed'; color: #9c9026} span.s1 {font-kerning: none} span.s2 {font: 9.0px 'Block Berthold'; font-kerning: none}

Distance du point M au cercle (C) de centre F et de rayon r.

On veut maintenant, étant donnés un point A et un cercle (C) de centre F et de rayon r, déterminer l'ensemble des points M équidistants du cercle (C) et du point A. 

Si le point A est extérieur au cercle (C) et si P est le point qui matérialise la distance du point M au cercle (C), écrire que MP = MA revient à écrire MF – r = MA, soit MF – MA = r. Dans ce cas, le point M décrit donc un arc d'hyperbole de foyers A et F d'axe transverse r et il n'y a aucun point M équidistant de A et de (C) qui soit strictement à l'intérieur du cercle (C).

Équidistante d'un point et d'un cercle : les deux cas.

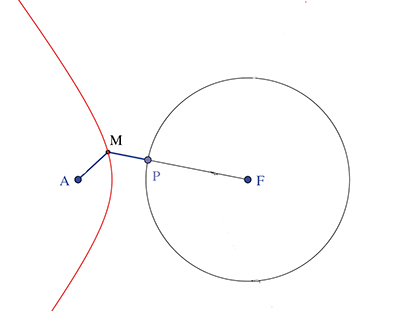
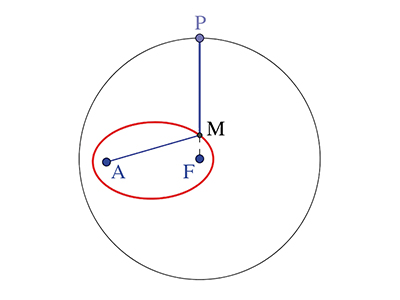
En effet, s'il y en avait un, il vérifierait MP = MA, soit r – MF = MA, ou encore MA + MF = r. Or MA + MF ≥ AF d'après l'inégalité triangulaire, mais AF < r : contradiction. Si le point A est intérieur au cercle (C), on a toujours MP = MA, avec MP = r – MF. C'est dire que MA + MF = r, et le point M décrit maintenant l'ellipse de foyers A et F et d'axe transverse r. Il n'y a ici aucun point M équidistant de A et (C) qui soit intérieur au cercle (C). Si un tel point existait, dire que MP = MA reviendrait à dire que MF – r = MA. Or MF ≥ MA + AF, donc MF – MA ≥ AF avec AF < r, nouvelle contradiction ! Dans les deux cas, la distance du point M au cercle (C) est égale à MP. Enfin, dans le cas extrême où A appartient au cercle (C), le seul point M convenable serait F. 

On peut aussi rechercher l'équidistante de deux cercles, (C) de centre F et de rayon r, (C') de centre F' et de rayon r'. Plaçons-nous par exemple dans le cas où les deux cercles sont extérieurs (FF' > r + r') et où r est supérieur à r'.

Ici, aucun point M ne peut être intérieur à (C) puisque l'on aurait MP = MP', ce qui équivaut à MF + MF' = r + r' alors que MF + MF' ≥ FF' > r + r'. Pour le même genre de raison, aucun point M ne peut être intérieur au cercle (C'). Alors, (C) et (C') étant extérieurs, MP = MP' équivaut à MF' – MF = r' – r, et le point M décrit un arc d'hyperbole de foyers F et F' et d'axe transverse | r' – r |.

Il en sera de même si les cercles sont tangents extérieurement.

S'ils sont intérieurs, l'ensemble sera constitué d'une ellipse et d'un arc d'hyperbole, et de même s'ils sont sécants.

S'ils sont tangents intérieurement en A, l'équidistante sera une ellipse de foyers F et F' et de grand axe r + r' (s'il sont tangents extérieurement en A, elle sera un arc d'hyperbole de foyers F et F' et d'axe transverse | r – r' |).

Des droites et bien d'autres figures…

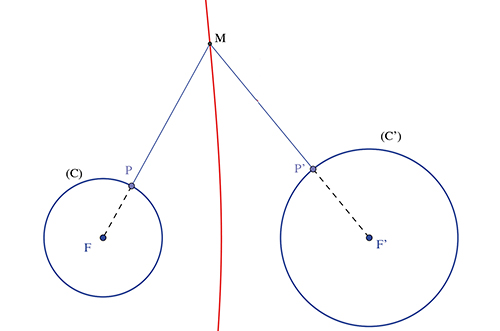
Équidistante de deux cercles extérieurs.

La droite, élément géométrique simple s'il en est, peut pourtant donner des cas de figure sophistiqués. Recherchons par exemple les équidistantes d'une droite d et d'un cercle (C) de centre F et de rayon r. Il nous faut alors considérer trois cas : (1) ou bien la droite est extérieure au cercle, (2) ou bien elle lui est tangente en A, (3) ou bien encore cercle et droite sont sécants en deux points A et B.

Équidistantes de deux cercles sécants.

Dans le cas (1), chercher l'ensemble des points M équidistants de d et du cercle (C) équivaut à écrire MP = MH, soit MF – r = MH, qui équivaut à MF = MH + r. En introduisant la droite d', à une distance r de d dans le demi-plan ne contenant pas F, et K le projeté orthogonal de H sur d', cela signifie que MF = MK. Le point M décrira donc la parabole de foyer F et de directrice d'.

Dans le cas (2), MP = MH équivaut à MF = MH + r. Même intervention de d', et on est amené à dire que M décrit la parabole de foyer F et de directrice d'. Elle passe d'ailleurs par A, à une distance nulle aussi bien du cercle (C) que de la droite d.

Dans le cas (3), enfin, MP = MH revient à dire, soit que MF = MH + r, et alors M est sur la parabole de foyer F et de directrice d', soit que MF = r – MH, et donc M est sur la parabole de foyer F et de directrice d''. Les tracés des équidistantes figurent en rouge dans les trois cas.

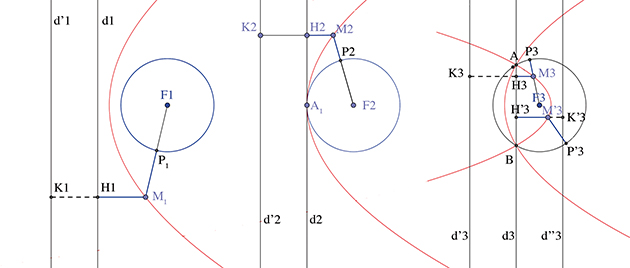
Équidistante d'une droite et d'un cercle, trois cas.

Et, pour terminer, pourquoi ne pas rechercher l'équidistante d'une droite et d'un carré ? Disposés comme sur la figure, ces deux figures permettent de partager le plan en huit zones, où les tracés des courbes réalisant l'équidistance sont totalement différents. Il nous faudra toujours tenir compte que la distance du point M au carré est la plus petite des distances de M aux points du carré.

Déjà, il n'existe à l'intérieur du carré aucun point équidistant de la droite et du carré. Nous désignerons par H le projeté orthogonal de M sur la droite d.

Pour les points M de la zone (I), le point du carré le plus proche de M est A et on devra réaliser MA = MH, si bien que M décrira un arc de parabole de foyer A et de directrice d.

Dans la zone (II), le point du carré le plus proche de M est son projeté orthogonal K sur le segment [AB], et on devra avoir MK = MH, si bien que M décrira une partie de la bissectrice des droites (AB) et d.

Dans la zone (III), le point du carré le plus proche de M est B ; réaliser MB = MH fait décrire à M un arc de la parabole de foyer B et de directrice d.

Aucun point M ne se trouve dans la zone (IV), la distance MH y étant toujours supérieure à celle de M au côté [BC].

Dans la zone (V), il faudra réaliser MC = MH et M se déplacera sur un arc de la parabole de foyer C et de directrice d.

Si M est dans la zone (VI), on retrouve, comme dans la zone (II), une partie de la bissectrice des droites (CD) et d.

Pour M dans la zone (VII), on retrouve, comme dans (I), un arc de parabole de foyer D et de directrice d.

Pour la zone (VIII) enfin, où M doit être équidistant de (AD) et de d, on trouve une partie de l'axe de symétrie de ces deux droites.

Le tout donne à ce lieu géométrique des points M équidistants du carré ABCD et de la droite d cette allure fragmentée. Si la droite d coupait le carré, l'aspect changerait encore. Les équidistantes n'ont pas fini de nous surprendre !

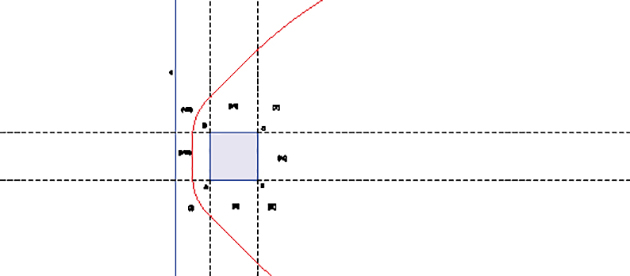
Équidistante d'une droite et d'un carré.