.jpg)
La notion de lieu géométrique semble naître avec Hippias d'Élis et sa construction mécanique d'une courbe obtenue comme le lieu du point d'intersection de deux segments mobiles, l'un en translation, l'autre en rotation. Cette courbe est appelée trisectrice, pour la résolution graphique de la trisection de l'angle, mais aussi quadratrice par Dinostrate, pour son utilité dans la quadrature du cercle. La strophoïde est, elle aussi, un lieu géométrique, c'est-à-dire un ensemble de points ayant tous la même propriété.
L'étude de cette famille de courbes, commencée au cours du XVIIe siècle, se retrouve dans les œuvres de nombreux physiciens mathématiciens, comme Evangelista Torricelli en 1644 et Gilles de Roberval. Ce dernier donnera à ces courbes, en 1645, le nom de ptéroïdes (« en forme d'aile »), qui sera conservé jusqu'à la fin du XVIIIe siècle. Elle sera renommée strophoïde (« en forme de torsade ») pour la première fois en 1837 dans un ouvrage du mathématicien italien Enrico Montucci de Sienne.
Des constructions multiples
D'une manière générale, une courbe strophoïdale est la courbe engendrée à partir d'une courbe f donnée et de deux points, un pôle O et un point fixe F, de la façon suivante : pour un point courant M de la courbe f , on détermine sur la droite (OM) les points P1 et P2 tels que M soit le centre du cercle passant par les points P1, P2 et F.
On a donc MP1 = MP2 = MF. Donnons pour exemple le cas d'un cercle C avec le pôle O sur sa circonférence et deux cas de points fixes, F1 au centre de C et F2 diamétralement opposé au pôle. Dans le premier cas, on obtient une conchoïde de cercle, puisque MF1 est constant et égal au rayon de C ; dans le second cas, chacun des points sur le rayon vecteur
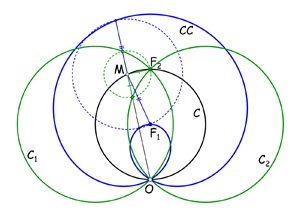
Courbes strophoïdales du cercle.
Dans le cas où la courbe génératrice est une droite sur laquelle se trouve le point fixe, on parle de strophoïde oblique, ou droite quand le point fixe est la projection du pôle sur la droite. La figure suivante illustre la construction d'une telle strophoïde oblique de pôle F, de point fixe (ou foyer singulier) l'origine O du repère orthonormé, et de courbe l'axe des ordonnées. Dans ce repère, l'équation d'une telle courbe est x(x2 + y2) – ax2 + ay2 – 2bxy = 0, où (a, b) sont les coordonnées du pôle F.
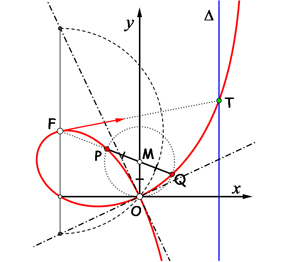
Strophoïde oblique.
Puisque le terme du troisième degré de cette équation est multiple du terme (x2 + y2), on parle de cubique circulaire, qui est de plus unicursale (d'un seul morceau). Et on nomme strophoïde toute cubique circulaire unicursale dont les tangentes au point double font un angle droit. Pour obtenir ces tangentes orthogonales au point double O, on le relie aux extrémités du diamètre du cercle de centre F passant par O parallèle à l'axe des ordonnées, et donc aussi à l'asymptote
En notant T le point d'intersection, qui peut être à l'infini, de la strophoïde avec son asymptote, la droite (FT) porte la tangente au pôle F.
Si la droite (OF) est perpendiculaire à l'axe des ordonnées, c'est-à-dire pour b = 0, l'équation devient x(x2 + y2) – ax2 + ay2 = 0. La courbe est symétrique par rapport à l'axe des abscisses ; on parle de strophoïde droite. Différentes méthodes de construction sont proposées dans la figure qui suit. Les points P et Q sont construits selon la définition précédente de la strophoïde en général, et sont donc tels que
où
La définition générale d'une strophoïde est donnée à partir de deux points et une courbe. Dans le cas où la courbe est une droite (strophoïde oblique ou droite), trois points peuvent suffire à la définir : pour trois points fixes A, B et O, le lieu des points M tels que la bissectrice de l'angle
Soient maintenant C et D deux points de la médiatrice de [AB], cocycliques avec A et B (donc situés sur le cercle (
Trouver la pierre angulaire
Les nombreuses propriétés des strophoïdes reposent fondamentalement sur la notion de points conjugués, c'est-à-dire tels que les droites les joignant au point double O sont également inclinées sur les tangentes en ce point double. Le couple de points (P, Q) de la figure suivante en est un exemple. Tout ceci explique l'importance des relations angulaires dans ces courbes.
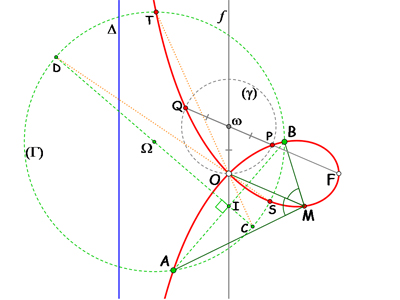
Strophoïde droite.
Pour continuer l'inventaire des constructions possibles d'une strophoïde droite, présentons l'exemple classique de la construction par un orthocentre : pour deux points fixes O et F, l'orthocentre H du triangle MOF, où M est un point courant du cercle de centre O passant par F, décrit une strophoïde droite de point double O et de pôle F.
Une fois comprise la pierre « angulaire » de ces constructions, on peut inventer d'autres méthodes caractérisant une strophoïde, comme la suivante : pour deux points fixes F et O, le centre I du cercle inscrit du triangle FON, où N est un point courant du cercle de centre F passant par O, décrit la boucle de la strophoïde droite de point double O et de pôle F. Le centre K du cercle exinscrit opposé au pôle F décrit les branches asymptotiques de cette même strophoïde. Remarquez que les deux autres centres des cercles exinscrits parcourent le cercle de centre F diamétralement opposés.
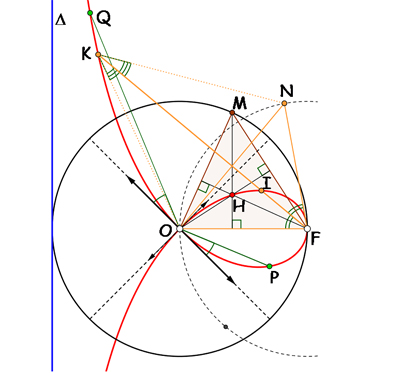
Autres méthodes de construction.
Ces propriétés maîtrisées permettent alors de comprendre, sans calculs, qu'une strophoïde peut être :
• le lieu des foyers des coniques tangentes en deux points donnés à deux droites données,
• le lieu des foyers des coniques tangentes à deux droites données et admettant pour directrice une droite donnée,
• une podaire : le lieu des pieds des perpendiculaires abaissées d'un point fixe de la directrice d'une parabole sur les tangentes à cette parabole.
Vous pouvez vérifier vous-mêmes, sans aucune difficulté, ces propriétés choisies à l'aide d'un magnifique outil prospectif, un logiciel de géométrie dynamique.