Qu'appelle-t-on un lieu géométrique ? Il s'agit en général de tous les points du plan (ou de l'espace) vérifiant une propriété donnée. La médiatrice de deux points A et B dans le plan en est un exemple élémentaire puisque c'est le lieu des points équidistants de A et de B. Plus subtilement, l'ellipse en est un autre, comme l'ensemble des points dont la distance à deux points F et F' est égale à une longueur a donnée (évidemment supérieure à la distance de F à F'). Mais alors, dira-t-on, toute courbe est un lieu géométrique ! En fait, pas tout à fait si l'on considère la définition actuelle d'une courbe par une équation abstraite quelconque… Par «lieu géométrique», on entend que l'expression soit explicite et puisse donc faire l'objet d'un tracé. De nombreuses approches permettent de définir de tels lieux géométriques. Brossons un tableau historique de l'évolution de cette notion.

 L'Antiquité et les Anciens

L'approche d'Euclide n'est pas tournée vers la recherche de lieux géométriques. Chez Apollonius, au contraire, de nombreux problèmes qu'il résout s'y apparentent. On connaît son intérêt pour les coniques ; il étudie ainsi les points desquels on peut tracer plusieurs normales à l'ellipse ou à l'hyperbole. Il obtient ainsi la développée de ces courbes.
Dans l'œuvre d'Archimède, on trouve de nombreux calculs d'aires. Cependant, la définition qu'il donne de la spirale qui porte son nom s'apparente au problème de recherche d'un lieu. Il considère une droite D tournant à vitesse constante autour d'un point O et un point M, partant de O et qui s'en éloigne à vitesse constante également (voir en encadré). Archimède nous propose ainsi l'un des premiers lieux géométriques défini par un problème cinématique !

Quatre siècles plus tard, Nicomède, qui vivait à Alexandrie, introduit la conchoïde pour tenter de résoudre, vainement, le problème de la trisection de l'angle. Il considère un point O, une droite D et une longueur m. Il fait tourner alors une droite  \( \Delta\) autour de O et, en notant P le point d'intersection de  \( \Delta\)  avec D, il considère les deux points Q et R de  \( \Delta\)  situés de part et d'autre de P et à une distance m de celui-ci (voir en encadré). Cette courbe a peu d'intérêt de nos jours ; elle reste cependant la première construction connue d'une courbe autre que la droite ou le cercle.

Courbes mécaniques et géométriques

La Géométrie de Descartes fut publiée en 1637 comme l'un des trois appendices du Discours de la méthode. Cet ouvrage est fondamental dans le développement des mathématiques. En premier lieu, c'est là que le savant introduit la géométrie analytique, c'est-à-dire l'utilisation de coordonnées pour mettre en équation les figures géométriques. Pour sa part, il préfère dire « Comment le calcul d'arithmétique se rapporte aux opérations de géométrie ». Descartes reprend alors des recherches de lieux géométriques proposés par les Anciens, Pappus ou Apollonius, avec un outil plus efficace. Il s'étonne de la qualification de « mécaniques » données à certaines courbes « par le fait qu'elles sont tracées par quelque machine, que l'on oppose à celles qu'on dénomme “géométriques” » parce qu'elles sont définies par le raisonnement et que les outils utilisés sont « un compas et une règle, qu'on peut aussi nommer des machines ». Il remarque en particulier que c'est la justesse du raisonnement qui importe, plus que les moyens effectifs de tracer.

Pour illustrer sa méthode, Descartes propose de nombreux exemples déjà traités dans l'Antiquité par d'autres moyens. Prenons l'un d'eux, déjà évoqué par Pappus : considérons quatre droites (AG), (GH), (EF) et (AD) du plan et un point C non situé sur l'une d'entre elles. Traçons alors les quatre droites passant par C et formant un angle spécifié par rapport à chacune d'entre elles (non forcément le même). Notons respectivement P, Q, R et S les points d'intersections de ces droites avec (AG), (GH), (EF) et (AD). Cherchons alors le lieu des points vérifiant l'égalité des produits scalaires \( \overrightarrow{\text{CP}}\cdot \overrightarrow{\text{CR}}= \overrightarrow{\text{CS}}\cdot \overrightarrow{\text{CQ}}\) . En appelant x la longueur AP et y CP, Descartes trouve une équation du second degré et vérifie que c'est une conique. Le résultat prouvé par Pappus est ainsi redémontré de manière beaucoup plus aisée !

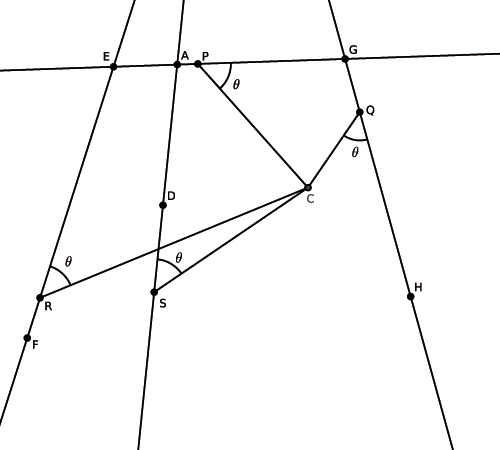
La construction de Pappus revisitée.

L'arrivée du calcul différentiel

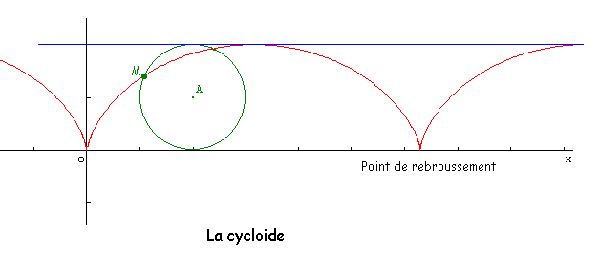
L'introduction du calcul différentiel et intégral est une nouvelle étape pour la recherche de lieux géométriques, en particulier ceux définis par des propriétés tirées de la cinématique ou de la physique. La notion d'équation différentielle permet la recherche de nouveaux lieux définis par des conditions d'optimisation : c'est la naissance du calcul des variations, qui amène à des équations différentielles. Jacques Bernoulli est l'un des premiers à proposer la recherche de la courbe suivant laquelle un pendule effectue une oscillation dans le même temps, quelle que soit son amplitude. Une solution analytique avait été proposée par Leibniz. Bernoulli aboutit à une équation différentielle qui lui permet de retrouver la cycloïde. Cette courbe, déjà étudiée par Roberval, attire à ce moment tous les regards. Il s'agit de la courbe qui peut être définie comme lieu des points décrit par un chewing-gum collé sur la roue d'un vélo…

En 1696, Jean Bernoulli lance un défi dans Acta Eruditorum pour donner la résolution de la « courbe brachistochrone ». Considérant deux points A et B, le premier étant plus élevé que le second, il s'agit de trouver la courbe suivie par un mobile mu par la pesanteur seule qui minimise le temps de parcours. Dans l'année qui suivit, Gottfried Leibniz, Isaac Newton, Guillaume de L'Hospital et Jacques Bernoulli proposèrent chacun une solution, toutes publiées l'année suivante dans la même revue. Jean Bernoulli fut émerveillé de voir que, cette fois encore, la réponse était un arc de cycloïde.

Le théorème de la Hire

Philippe de la Hire (1640–1718) se destinait à une carrière d'artiste peintre. Pour améliorer son art, il voyage en Italie et cherche à parfaire ses connaissances dans le domaine de la perspective. Ceci l'amène à étudier la géométrie et à tant y prendre goût qu'il s'y consacre ; il obtient la chaire de mathématiques au Collège royal (aujourd'hui Collège de France). Son intérêt se porte sur les sections coniques, au point qu'il publie un ouvrage sur ce thème en 1675.

On donne en France le nom de théorème de La Hire à un résultat mis en évidence bien avant lui par le savant persan Nasir ad-Din al-Tusi (1201–1274) et par le mathématicien italien Jérôme Cardan (1501–1576) ; le mathématicien français en a donné une démonstration nouvelle, ce qui explique son nom en France.

Faisons rouler un cercle de rayon r à l'intérieur d'un cercle de rayon 2r. Alors un point du petit cercle décrit un diamètre du grand. Ce résultat permet en mécanique de transformer un mouvement circulaire en mouvement rectiligne.

Philippe de la Hire s'est intéressé aussi à la courbe orthoptique d'une conique G. On nomme ainsi l'ensemble des points du plan desquels on peut tracer deux tangentes à G faisant un angle droit entre elles. L'orthoptique d'une parabole est tout simplement sa directrice. L'orthoptique d'une ellipse ou d'une hyperbole est un cercle appelé cercle de Monge.