L'invention de la machine à vapeur relance un vieux problème : comment transformer la translation du piston, poussé par la vapeur, en rotation ? C'est une question qui remonte au moins à l'utilisation des moulins à eau : il fallait souvent transformer la rotation de la roue en un mouvement linéaire, ce qui est en fait le problème inverse. James Watt (1736–1819) donnera une solution approchante. Charles Peaucellier (1832–1919) et Lipman Lypkin (1846–1876) donneront une solution exacte en 1864, suivis de Harry Hart en 1875 et Alfred Kempe en 1876 (qui est essentiellement connu pour sa « preuve » finalement erronée du théorème des quatre couleurs).

 
Une machine pour imiter votre signature

Or, faire des maths, c'est aussi généraliser. C'est ce que fait Kempe : il montre que l'on peut non seulement tracer des droites avec des systèmes articulés, mais qu'en outre toute courbe algébrique peut être tracée avec un mécanisme de type système articulé (c'est-à-dire des barres rigides reliées entre elles par des articulations de type pivot). Ce résultat extraordinaire est le théorème d'universalité de Kempe. L'immense géomètre américain William Thurston (1946–2012) avait ainsi résumé, lors d'une conférence : « Si votre signature est une suite continue de courbes (vous ne levez pas le stylo) alors il existe un mécanisme pouvant exécuter votre signature ! » Après, il faudra peut-être des centaines de barres à la machine…

Revenons au mécanisme découvert par James Watt en 1784. S'il ne permet que d'approximer la droite autour du point d'inflexion, il permet de tracer une magnifique lemniscate de Bernoulli.
Ici, AC = BD et AB = CD = \( \sqrt{2}\)   AC, le point E étant le milieu de [CE] (les points A et B sont des points fixes, en bleu, C et D sont des articulations, en mauve). Le point E parcourt la lemniscate lorsque le point C tourne autour de A.

De nombreux mécanismes vont servir à tracer des coniques. Frans van Schooten (1615–1660) publie dans son De Organica Conicarum Sectionum (en 1646) plusieurs constructions. Il commence par la méthode du jardinier pour l'ellipse. Puis il construit l'ellipse : le losange OIPG possède un point fixe I (foyer de l'ellipse) quand P tourne autour de I. Le point courant de l'ellipse est donné par l'intersection des droites (HG) et (OP).

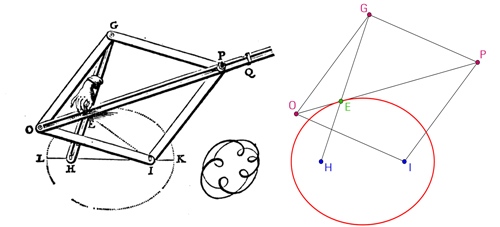
La construction de van Schooten de l'ellipse.

 Pour construire l'hyperbole, on procède ainsi : le losange DMFL possède un point fixe F. Quand C tourne autour de D, l'intersection des droites (CD) et (LM) donne le point courant de l'hyperbole.

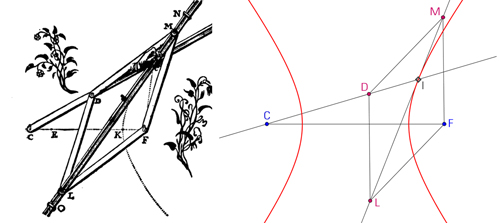
La construction de van Schooten de l'hyperbole.

Enfin, pour la parabole, le losange FGHB est articulé au point fixe B. Quand la règle [AD] glisse, perpendiculairement à son axe, l'intersection de la droite (FH) et (AD) donne le point courant D.

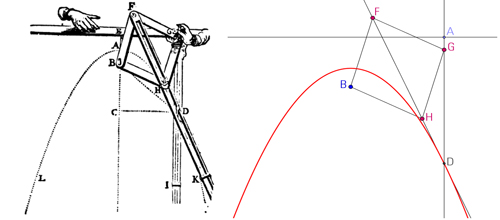
La construction de van Schooten de la parabole.

 
Le nec plus ultra : le mécanisme articulé

Les constructions de van Schooten, bien que très astucieuses, ne sont pas des constructions par systèmes articulés à proprement parler. En effet, on n'y utilise que des glissières, ou alors le pointeur se trouve à l'intersection de deux glissières. Voici un exemple de mécanisme réellement articulé :

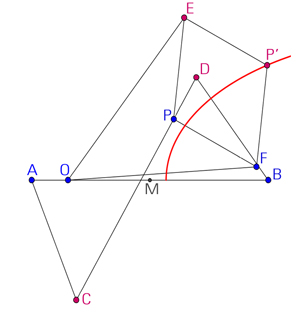
Système articulé
traçant des coniques.

M est le milieu de AB, AB = CD, AC = BD, P se trouve sur la barre [CD] à une distance fixe de D. Quand C tourne autour du point A, P' parcourt une conique (ellipse, parabole ou hyperbole) ; la nature de la conique dépend du positionnement du point O et du rapport AB / AC. Il faut déjà neuf barres pour une conique, alors que le parallélogramme croisé suivant n'en nécessite que quatre (mais ce n'est pas un système articulé) :

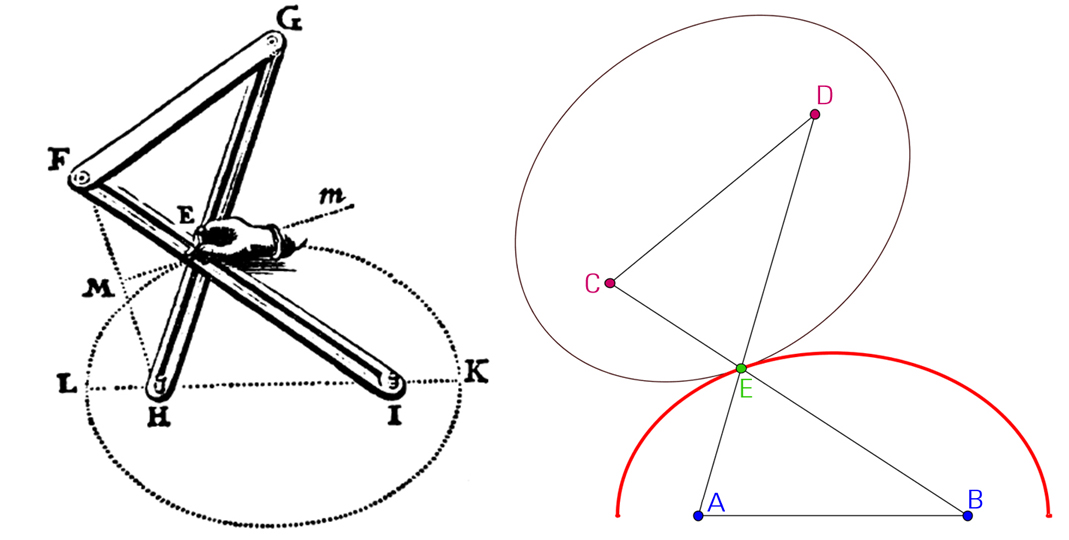
Le parallélogramme croisé. À droite, la version de van Schooten.
À gauche, lorsque C tourne autour de B, l'intersection des droites (AD) et (CD) parcourt une ellipse. 

Kempe avait proposé une méthode générale pour construire le système articulé correspondant à une courbe donnée. Mais le résultat était souvent excessivement sophistiqué. Matteo Gallet, Christoph Koutschan, Zijia Li, Georg Regensburger, Joseph Schicho et Nelly Villamizar proposent un nouvel algorithme pour les courbes paramétriques (Planar Linkages Following a Prescribed Motion, Mathematics of Computation 86, 2016). Cela conduit, pour une ellipse, à un mécanisme avec seulement huit barres et dix articulations :

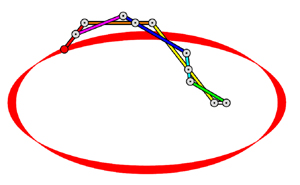
 Une ellipse avec un système articulé de huit barres.

Plus impressionnant, le système articulé suivant de vingt-six barres et trente-sept articulations trace le « J » de la signature de John Hancock, signataire de la déclaration d'indépendance des États-Unis, prenant ainsi au mot William Thurston…

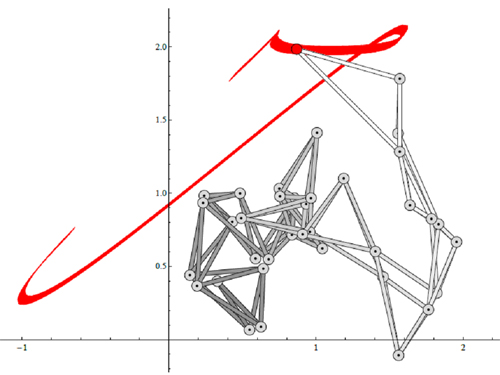
Le mécanisme traçant le J
de la signature de John Hancock.

Les systèmes articulés n'en finissent pas d'inspirer les mathématiciens ! Les travaux de Kempe ont trouvé une nouvelle jeunesse chez Thurston. Les informaticiens ont trouvé des méthodes pour générer automatiquement les mécanismes appropriés à chaque courbe, aussi sophistiquée soit-elle (de manière concrète, grâce au théorème de Weierstrass, toute courbe continue peut être approximée par un polynôme). Ces travaux auront des répercutions considérables en robotique.