Si vous êtes curieux, vous aurez sans doute remarqué une courbe étrange dans votre bol du petit-déjeuner. On peut la retrouver en posant une bague sur sa main ou au sol. Faites l'expérience : vous ne pourrez plus l'oublier ! On s'en aperçoit vite : ce phénomène est créé par la réflexion des rayons lumineux sur un cercle, mais… quelle est cette courbe ? Peut-on déterminer son équation et ses propriétés ?

Quand les rayons se focalisent

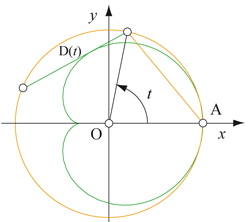
Il est aisé d'étudier la famille des rayons lumineux réfléchis sur un cercle. On trace les rayons venant du soleil, puis les rayons réfléchis sur le cercle. Le lien entre les deux est simple : elles font des angles égaux avec la normale au cercle au point d'incidence. Si l'on choisit comme axe des abscisses la droite orientée vers le soleil, on obtient le schéma suivant.

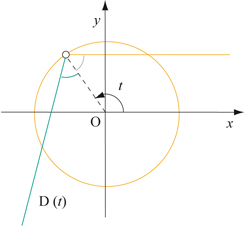
Les rayons venant du soleil (en orange)
sont réfléchis (en vert) sur le cercle. 

L'ensemble des rayons réfléchis sur le cercle de centre O et de rayon R peut être paramétré en fonction de l'angle polaire t du point d'incidence sur le cercle. On obtient une droite D(t) d'équation x sin 2t – y cos 2t – R sin t = 0. En traçant cette famille de droites à l'aide d'un logiciel graphique, voici ce que l'on observe :

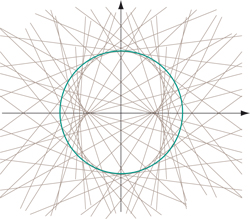 Tracé de la famille des rayons réfléchis.

Les rayons réfléchis se focalisent sur une courbe \( \Gamma\) . Plus précisément, la focalisation a lieu en des points où les droites D(t) sont tangentes à  \( \Gamma\) . Cette remarque suffit pour déterminer des équations paramétriques de la caustique du cercle. On obtient le paramétrage suivant de la courbe cherchée :

  \( \left\{ \begin{array}{ll} x(t)=\text{R}\left(\text{sin}\,t \:\text{sin}\,2t +\dfrac {\text{cos}\,t \:\text{cos}\,2t}{2} \right),\\\\ y(t)=\text{R}\left(\text{-sin}\,t \:\text{cos}\,2t +\dfrac {\text{cos}\,t \:\text{sin}\,2t}{2} \right). \end{array} \right.\)

Pour le démontrer, cherchons l'enveloppe de la famille de droites D(t), c'est-à-dire la courbe 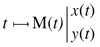 \( \Gamma\)  de paramétrage       telle que,

pour tout t, D(t) soit tangente à   \( \Gamma\)  en M(t).

Cette courbe est donc telle que M(t) \( \in\) D(t) et

\( \dfrac{d{\overrightarrow{\text{M}}}} {{\text{d}}t}(t)\in {\overrightarrow{\text{D}}}(t)\)  

pour tout t.

Ces deux conditions s'écrivent : 

  \( (\text{S})\left\{ \begin{array}{ll} x(t)\,\text{sin}\,2t\,- y(t)\,\text{cos}\,(2t)\,- \text{R}\,\text{sin}\,t=0, \\\ x'(t)\,\text{sin}\,2t\,- y'(t)\,\text{cos}\,(2t)\,=0. \end{array} \right.\)

En dérivant la première égalité de (S) et en soustrayant la seconde, on montre que S implique (S') :

  \( (\text{S'})\left\{ \begin{array}{ll} x(t)\,\text{sin}\,2t\,- y(t)\,\text{cos}\,(2t)\,- \text{R}\,\text{sin}\,t=0, \\\ 2x(t)\,\text{cos}\,2t\,+ 2y(t)\,\text{sin}\,(2t)\,- \text{R}\,\text{cos}\,t=0. \end{array} \right.\)  

Réciproquement, (S') implique également (S), donc les deux systèmes sont équivalents. Le second se résout en  

\( \left\{ \begin{array}{ll} x(t)=\text{R}\left(\text{sin}\,t \:\text{sin}\,2t +\dfrac {\text{cos}\,t \:\text{cos}\,2t}{2} \right),\\\\ y(t)=\text{R}\left(\text{-sin}\,t \:\text{cos}\,2t +\dfrac {\text{cos}\,t \:\text{sin}\,2t}{2} \right). \end{array} \right.\)

qui constitue donc un paramétrage de la courbe  \( \Gamma\)  cherchée.

Un logiciel graphique permet de la tracer, en faisant varier t sur un intervalle d'amplitude 2 \( \pi\) .

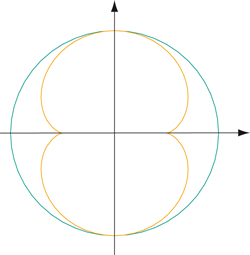
Enveloppe de la famille des rayons réfléchis.

On trouve la courbe aperçue dans notre bol de petit déjeuner, plus sa symétrique par rapport à l'axe vertical ! Rien de plus naturel : cette partie correspond à des rayons lumineux se réfléchissant sur la partie droite du bol. Ceci ne peut se produire, du fait de l'opacité de la tasse. L'étude confirme notre analyse : il s'agit bien de l'enveloppe des rayons réfléchis sur un cercle.

La courbe  \( \Gamma\)  trouvée a été baptisée néphroïde à cause de sa ressemblance à un rein (on retrouve la racine grecque nephros dans le terme « colique néphrétique »). En utilisant les formules de trigonométrie, on peut simplifier son paramétrage :

\( \left\{ \begin{array}{ll} x(t)=\dfrac{\text{R}}{4}(3{\text{cos}}\,t-{\text{cos}}\,3t),\\\\ y(t)=\dfrac{\text{R}}{4}(3{\text{sin}}\,t-{\text{sin}}\,3t). \end{array} \right.\)  

Ces équations sont celles d'une épicycloïde, c'est-à-dire le lieu du point d'un cercle roulant sans glisser sur un autre. Dans le cas de la néphroïde, le cercle roulant a un rayon moitié de celui du cercle fixe.

Si la source lumineuse est sur le cercle, on obtient une cardioïde, qui est une autre épicycloïde. Celle-ci est obtenue en faisant rouler sans glisser un cercle sur un cercle de même rayon.

 

Quand le cercle de centre Ω roule sans glisser sur le cercle de centre O et de rayon double, il décrit une néphroïde. Les calculs se font en remarquant que l'angle  \( \widehat{\textbf{T}\Omega\textbf{M}}\) est le double de l'angle \( \widehat{\textbf{OAT}}\) .

On obtient une droite D(t) d'équation x cos(3t / 2) + y sin(3t / 2) – R cos(t / 2) = 0. En appliquant la même méthode que dans le cas de la caustique au soleil, on aboutit à l'équation :

\( \left\{ \begin{array}{ll} x(t)=\text{R}\left((\text{cos}\,t/2) \:(\text{cos}\,3t/2) +\dfrac {(\text{sin}\,t/2) \:(\text{sin}\,3t/2)}{3} \right),\\\\ y(t)=\text{R}\left((\text{cos}\,t/2) \:(\text{sin}\,3t/2) +\dfrac {(\text{sin}\,t/2) \:(\text{cos}\,3t/2)}{3} \right). \end{array} \right.\)   

Mais quel est le rapport entre les caustiques, la soude et une personne acerbe ? En français, le mot « caustique » est utilisé dans trois contextes très différents. Dans le langage courant, on parle d'esprit caustique, ce qui désigne un esprit sarcastique, acerbe. En chimie, la soude est dite caustique, c'est-à-dire corrosive. Le sens semble encore différent en optique et en mathématiques, où il s'agit de l'enveloppe de rayons lumineux réfléchis. Comme souvent dans un cas pareil, le point commun vient du grec, du mot kaustikos, qui signifie « qui peut brûler » et qui réunit bien les trois sens évoqués (puisque la focalisation des rayons lumineux sur une courbe peut la rendre brûlante). On retrouve la même étymologie dans le verbe « cautériser », un terme de médecine qui signifie « brûler » (chimiquement, de nos jours) une plaie pour arrêter les saignements ou prévenir une infection.

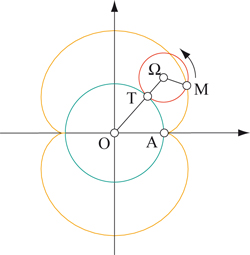
Les rayons venant du point A
sont réfléchis sur le cercle.