La gestion de stocks a donné naissance depuis cinquante ans à une littérature abondante, multipliant les modèles. Pour chaque problème, il faut déterminer dans quel contexte on va travailler de manière à traduire le plus correctement possible la réalité. Il faut choisir entre un modèle à court terme ou long terme, opter pour un contexte déterministe ou aléatoire, définir des principes de gestion optimale. Il faut enfin paramétrer le modèle de manière réaliste, ce qui n'est pas la partie la plus simple du problème.

Le paramétrage du problème

On désire ajuster la production (ou constituer un stock ou un approvisionnement idéal) à un horizon fini T. Pour cela, on considère un approvisionnement initial unique d'une quantité déterminée Q, constitué à l'instant 0, d'un certain produit P devant satisfaire la demande durant l'intervalle de temps [0, T[. Quel que soit le stock originel, deux situations peuvent se produire : 

• la demande est inférieure au stock Q (existence d'un stock résiduel) 
• elle se révèle supérieure (rupture de stock). 

On peut admettre que pour le très court terme, le type d'écoulement, qui n'est pas nécessairement linéaire, n'a pas d'incidence sur l'optimalité du système de gestion. Cela constitue d'ailleurs la définition du court terme. On peut alors se contenter d'une modélisation qui repose uniquement sur la situation initiale et la situation finale de la fonction « stock résiduel ».  

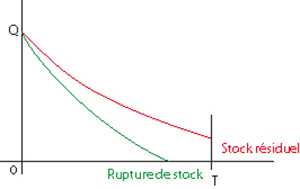
La fonction stock résiduel dans les deux cas.

Pour paramétrer la quantité de biens en demande durant cette période, on note R la variable aléatoire demande, dont on suppose la distribution connue, de fonction de répartition F(r). 

Ces hypothèses ont l'air naturelles, elles sont déjà très fortes : la distribution de probabilité de la variable aléatoire demande n'est jamais entièrement maîtrisée, elle peut au mieux être approchée. Il convient d'ailleurs de distinguer la variable demande de la variable vente, la demande pouvant être supérieure à l'offre. La vente peut être vue comme la demande, assortie d'une « barrière absorbante en 0 ». 

Pour le produit P, on appelle :

• c le coût de production marginal unitaire ;

• s le prix de vente unitaire ;

• v la valeur unitaire résiduelle à l'instant T des éléments du solde (invendus) ;

• p la perte unitaire subie en cas de demande supérieure à l'offre (coût d'opportunité) ;

• a les coûts fixes de production. 

Dans le contexte, ils n'influencent pas le système de gestion, la décision n'étant pas au niveau de la variable « produire ou non », mais au niveau marginal « produire plus ou moins ». 

On doit avoir s > c > v. Dans le cas contraire, une production exorbitante, ne correspondant en rien aux besoins du marché, serait modélisée comme un accroissement de richesse. 

Le mathématicien a l'illusion d'avoir bien modélisé le réel. Le gestionnaire est moins à l'aise : il sait que toutes ces valeurs numériques sont loin d'être aisées à déterminer concrètement. 

Un principe d'optimalité qui dépend des objectifs

La définition du principe d'optimalité a une influence significative sur le type de gestion. Ce choix relève du décideur. Il peut opter pour une gestion prudente, minimisant le risque de perte, ou préférer une gestion plus agressive dans le but de maximiser son profit. Il peut aussi se fixer un niveau de risque de rupture de stock à ne pas dépasser de façon à ne pas mécontenter le client.

La distribution de la demande R sur [0, T[ devrait avoir une fonction densité de probabilité f (r) nulle pour toute valeur négative de r. On constate cependant que les gestionnaires travaillent couramment avec une fonction de demande normale, définie pour tout r réel. Il convient alors de conforter la pertinence de l'hypothèse de normalité en vérifiant que la probabilité associée à l'ensemble des valeurs négatives n'est pas significativement différente de zéro. 

Lorsque ce n'est pas le cas, on peut travailler avec d'autres types de distribution : uniforme, exponentielle négative, ou de type Erlang. 

Lorsque la demande est inférieure à l'offre (r < Q), le gestionnaire se retrouve à l'instant T face à un stock résiduel (Q – r) qu'il ne peut plus négocier dans les mêmes conditions. C'est le cas pour des denrées périssables, mais également aussi pour tous les articles de mode. Il en résulte avec les notations précédentes une perte unitaire du résidu C₁ = c – v. 

Lorsque la demande est supérieure à l'offre (r > Q), le gestionnaire peut rater des ventes ou être contraint de faire appel à la sous-traitance. Il en résulte un coût unitaire marginal quantifiable  C₂ = p. 

Plusieurs politiques sont alors envisageables. Deux d'entre elles sont explicitées ci-après.

La première (calcul en encadré) consiste à minimiser l'espérance de la variable coût total, la deuxième à maximiser celle du profit. 

Dans tous les cas, la solution au problème n'est pas explicite : elle passe par le canal de la fonction de répartition de la variable demande. Ce gage de réalisme était intuitivement prévisible. La solution n'est pas une quantité à produire mais une probabilité de production ou d'approvisionnement suffisante pour faire face à la demande. 

La fonction de répartition F(Q) représente la probabilité, optimale selon le critère du minimum de coût, avec laquelle la demande doit être inférieure à la production, permettant ainsi de satisfaire tous les clients. Pour déterminer une quantité optimale à produire, il faut avoir une bonne idée de la répartition des ventes. Cette répartition peut changer d'un jour à l'autre de la semaine (journaux) ou d'une heure à l'autre dans la journée (hamburgers en restauration rapide). La probabilité complémentaire  représente la probabilité de rupture de stock en cas d'approvisionnement idéal. L'optimalité du système d'approvisionnement peut être testée. On tombe sur une application réaliste du théorème de Moivre-Laplace. Chaque approvisionnement représente une expérience aléatoire à deux issues possibles : stock résiduel ou rupture de stock. La répétition des approvisionnements dans des conditions comparables illustre un schéma de Bernoulli réaliste et l'on peut aisément vérifier l'optimalité du système d'approvisionnement ou de production. Le court terme du modèle conduit rapidement à un nombre suffisant d'expériences autorisant raisonnablement l'utilisation des lois faibles des grands nombres.

Optons à présent pour une politique plus agressive. Supposons que le gestionnaire désire maximiser son espérance de profit. Avec les notations de l'article, l'espérance de profit vaut :

\( E[P(Q)]=\int_0^Q[(s-v)r+vQ]f(r)dr+\int_Q^{\infty}[(s+p)Q-pr]f(r)dr-a-cQ.\)

En cas de stock trop important (r < Q), le flux financier engrangé est donné par la différence entre les rentrées consécutives aux ventes ajoutée à la valeur résiduelle du stock à terme, et le coût total de production (variable + fixe) :
P [Q | r] = sr + v (Q – r) – a – cQ. En cas de rupture de stock, on trouve P [Q | r] = sQ – p (r – Q) – a – cQ
selon le même raisonnement. Il convient en effet d'acter le coût d'opportunité pour toutes les ventes ratées pour cause de stock insuffisant. On utilise une nouvelle fois la formule de Leibniz pour arriver à la solution implicite :

\( F(Q)=\frac{s+p-c}{s+p-v}.\)

On vérifie que cette dernière probabilité de stock suffisant est toujours supérieure à la précédente, sous les hypothèses économiquement raisonnables (s > c > v). Une définition plus agressive de l'optimalité conduit à un excédant de production.

Un cas concret : la production de croissants le dimanche

Le cas particulier de la production de denrées périssables permet une illustration simple. Envisageons la production ou l'approvisionnement d'un bien produit ou fourni au prix unitaire c et vendu au prix unitaire s = (M + 1).c 

Le paramètre réel positif M représente la marge bénéficiaire en dehors, calculée sur le prix à la production. Cette dernière n'est pas le bénéfice unitaire réalisé : les frais fixes ne sont pas pris en compte et le problème traité se situe au niveau de la production marginale. Les produits périssables sont ceux de valeur résiduelle nulle (v = 0), ce qui est le cas de nos croissants du dimanche... chez un bon boulanger. Pour des produits à durée de vie courte, pour lesquels on n'envisage pas de possibilité de réapprovisionnement, on peut avancer que p = M.c 

Sous le principe du minimum de l'espérance de coût, la fonction de répartition de la demande correspond à l'optimum lorsque

\( F(Q)=\frac{p}{c-v+p}=\frac{Mc}{c-0+Mc}=\frac{M}{M+1}\)

On peut étudier cette fonction de la marge bénéficiaire M et constater qu'elle est strictement croissante sur l'ensemble des réels positifs, et de concavité vers le bas. Son image est bien conforme à celle d'une fonction de répartition : [0, 1[. 

Elle représente la probabilité avec laquelle on doit satisfaire la demande en cas de gestion optimale frileuse, exprimée en fonction de la marge bénéficiaire choisie. Une marge plus élevée correspond toujours à un taux de rupture plus bas (intuitivement évident) et situe le gestionnaire dans un contexte plus stable. 

Le comportement asymptotique, \( \lim_{M\to\infty}F (Q) = 1\) , signifie que pour des marges bénéficiaires élevées, on tendra à satisfaire la demande avec probabilité 1. Pour de fortes marges, la probabilité idéale de rupture de stock est proche de zéro. Dans le cas du maximum de l'espérance de profit, les choses sont à peine différentes. On calcule :

\( \begin{array}{l l} F(Q) &=\frac{s+p-c}{s+p-v} \\ &=\frac{(M+1)c+Mc-c}{(M+1)c+Mc-0}\\ &=\frac{2M}{2M+1} \end{array}\)

Voyons ce qu'il en est de nos croissants en tablant sur une marge bénéficiaire de 100 % (M = 1), les croissants étant vendus à deux fois leur prix de production. Une politique frileuse satisfera tous les clients avec probabilité 1/2. Une politique plus agressive fera grimper cette probabilité à 2/3. La quantité à produire dépendra évidemment de la distribution des ventes, le vrai problème consistant à déterminer celle-ci. Pas évident d'être boulanger !