La courbe L de Lorenz

Pour décrire les inégalités des revenus, l'économiste américain Otto Lorenz, alors âgé de 29 ans, introduit en 1905 la courbe qui porte désormais son nom. Pour une population et une donnée s'y référant, par exemple les revenus, la courbe de Lorenz est celle qui, à la part x des ménages les moins riches, associe le pourcentage y du revenu total qu'ils perçoivent. On obtient ainsi une courbe qui vaut 0 en 0, 1 en 1 et qui se situe au-dessous de la première bissectrice (droite d'équation y = x). En effet, le total des revenus de la moitié des gens les moins riches est inférieur à la moitié du total des revenus !

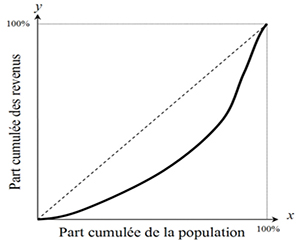
Cette courbe permet de visualiser comment la masse des revenus se répartit entre pauvres et riches. Plus la courbe s'éloigne de la première bissectrice, plus la répartition des revenus est inégale. Inversement, avec une répartition totalement égale, la courbe serait confondue avec la bissectrice.

De fait, pour tracer la courbe de Lorenz, on est amené à répartir les revenus par tranches progressives de revenus ; on obtient alors une ligne polygonale, qui est une bonne approximation.

L'indice G de Gini, une mesure de l'inégalité des revenus

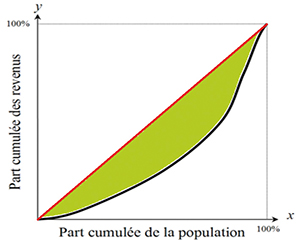
Formellement, l'indice G introduit par le statisticien démographe et ethnologue italien Corrado Gini (1884–1965) peut se définir à partir d'une courbe de Lorenz L (voir ci-contre) au moyen l'expression

\( G=2\left(\frac{1}{2}-\int_0^1L(p)dp\right).\)

On peut en donner une interprétation simple. En effet, l'intégrale ci-dessus mesure l'aire de la région située entre la courbe de Lorenz et l'axe horizontal, pour des abscisses variant entre 0 et 1. Le facteur 1/2 qui apparaît vaut la moitié de l'aire du carré représenté sur le graphe ci-contre. En conséquence, l'indice G est le double de la mesure de l'aire (en vert) comprise entre le segment dit d'équirépartition y = x et la courbe de Lorenz. Lorsque G = 0, c'est que la courbe de Lorenz se confond avec ce segment, indiquant une répartition totalement équitable des revenus dans la population. Lorsque G = 1 par contre, notre courbe de Lorenz s'identifie au segment de droite reliant l'origine et le sommet inférieur droit du carré, trahissant la mise à disposition de tous les revenus au profit d'un seul individu. Plus l'indice de Gini est élevé et proche de 1, plus grande est l'inégalité des revenus.

Un exemple numérique en Belgique

En pratique, l'indice de Gini se calcule en considérant simultanément les fréquences cumulées de la distribution des contribuables et celles des montants des revenus. Voici un exemple numérique, basé sur des données belges datant de 2002.

L'étude conjointe de ces deux distributions cumulées permet d'observer que les 20 % des individus déclarant les plus petits revenus gagnent ensemble environ 5,5 % de la masse totale des montants déclarés. Pire : les 50 % des salaires les plus bas n'arrivent pas à cumuler un quart de la masse totale des montants déclarés ! L'intégrale de la courbe de Lorentz se traduit par un calcul de somme d'aires de trapèzes et livre G = 0,389.