La variable aléatoire, histoire de faire du chiffre

 Il arrive que l'information brute accumulée soit de nature qualitative. Il arrive aussi qu'une information quantitative doive être transformée. C'est ici qu'intervient la notion de variable aléatoire, qui peut être vue soit comme une association numérique à des observations qualitatives, soit comme une transformation d'observations chiffrées.

Notons Ω l'ensemble de toutes les modalités ou valeurs que l'on peut associer à un phénomène aléatoire : à chaque élément v de Ω, on fait correspondre une valeur numérique x (ω). Cette association peut prendre en compte un nombre fini de valeurs possibles. On parle alors de variable aléatoire discrète. Si toutes les valeurs d'un intervalle, borné ou non, de la droite réelle peuvent être mises en correspondance avec les observations brutes, on obtiendra une variable aléatoire continue.

Fonction densité et fonction de répartition

Prenons une variable aléatoire continue. Pour présenter un grand nombre d'observations presque toutes différentes et parfois fort semblables, on réunit les valeurs « proches » dans un regroupement en classes ou intervalles. Cette procédure est arbitraire, même si l'on pratique honnêtement. On compte le nombre d'observations de chaque classe C_i et on leur associe des fréquences f_i (nombre d'observations de C_i divisé par nombre total d'observations). Le choix arbitraire des classes, éventuellement de longueurs différentes, rend la notion de fréquence peu intrinsèque. On introduit la densité de fréquence, ou fréquence par unité de mesure, d_i = (fréquence classe i) / (longueur classe i) = f_i / l_i , qui permet la construction d'une fonction densité en posant f (x) = d_i si x [ C_i. Ceci conduit, graphiquement, à la représentation d'une fonction en escaliers.

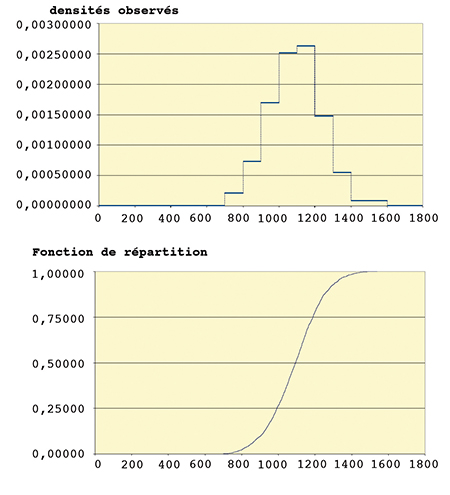
En associant à chaque observation x la fréquence des observations inférieures, on construit aussi une fonction de répartition observée F (x). Les notations f et F ne sont pas arbitraires ; en basant F sur un tableau de valeurs regroupées avec densité constante, la fonction F ainsi construite est une primitive de f.

Les « khi carrés » (ou « khi deux »), ou comment valider un modèle 

Comment bien modéliser un ensemble d'observations ? Et surtout, comment valider un modèle ? Le test du khi carré répond à cette dernière question en proposant un modèle probabiliste mesurant les différences entre valeurs observées et valeurs attendues lorsque ces différences sont purement aléatoires et ne reflètent pas une erreur systématique due à un mauvais choix lors de la modélisation. Sous certaines hypothèses, la somme des carrés des écarts entre valeurs observées et valeurs théoriques, relativement à ces mêmes valeurs théoriques, suit une distribution type, tabulée, constituée d'une somme de carrés de distributions normales réduites indépendantes : la distribution χ². Le nombre de termes indépendants de la somme détermine le degré de liberté de la distribution. La même distribution permet également de tester pragmatiquement l'indépendance entre deux séries d'observations. Un outil indispensable donc !