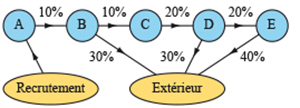
Comment les chaînes de Markov et donc les mathématiques peuvent-elles s'introduire dans la gestion du personnel d'une entreprise ? Voyons-le sur un exemple. Il s'agit de l'évolution des carrières des cadres d'une grande entreprise, dont l'effectif est supposé constant, disons 5 700 employés. Il y existe cinq niveaux hiérarchiques, notés A, B, C, D et E. L'évolution annuelle de chaque cadre est schématisée dans le diagramme suivant :

Représenter les stratégies d'entreprise

La constance des effectifs signifie que le recrutement annuel équivaut, en nombre, les départs vers l'extérieur. De plus, d'après le schéma, chaque année, 10 % des effectifs du niveau A est promu au niveau B, 10 % de B au niveau C, tandis que 30 % quitte l'entreprise, et ainsi de suite. Il s'agit d'un exemple de chaîne de Markov et, de l'extérieur, les pourcentages peuvent être vus comme des aléas, même si individuellement les promotions ne sont pas aléatoires.

Si on note a_n, b_n, c_n, d_n et e_n les effectifs respectifs des niveaux A, B, C et D à l'année n, le schéma précédent se traduit par les relations de récurrence suivantes :

\( \left\{ \begin{array}{l} a_{n+1}=0,9a_n+0,3b_n+0,3d_n+0,4e_n\\ b_{n+1}=0,1a_n+0,6b_n\\ c_{n+1}=0,1b_n+0,8c_n \\ d_{n+1}=0,2c_n+0,5d_n \\ e_{n+1}=0,3d_n+0,6e_n \end{array} \right.\)

ce qui s'écrit matriciellement X_n+1 = X_n A, où X_n est la matrice ligne de composantes a_n, b_n, c_n, d_n, et e_n et A la matrice carrée suivante : 

\( A=\begin{pmatrix} 0,9 & 0,1 & 0 & 0 & 0 \\ 0,3 & 0,6 & 0,1 & 0 & 0 \\ 0 & 0 & 0,8 & 0,2 & 0 \\ 0,3 & 0 & 0 & 0,5 & 0,2 \\ 0,4 & 0 & 0 & 0 & 0,6 \\ \end{pmatrix}.\)

La notation de X_n en ligne n'est pas usuelle dans le cadre de l'algèbre (où X_n serait plutôt noté en colonne) mais est courante dans le domaine des chaînes de Markov. Le lien entre les deux se fait par transposition ^tX_n+1 = ^tA × ^tX_n. Cette matrice A est la matrice de transition de la chaîne de Markov. Par récurrence, X_n = X₀ × Aⁿ. En utilisant les valeurs propres de la matrice A (voir en encadré), on s'assure que X_n possède une limite L, où L est un vecteur propre de ^tA associé à la valeur propre 1.

L'égalité des polynômes caractéristiques de A et de sa transposée prouve que cette valeur propre est simple, c'est-à-dire que l'espace propre associé à 1 est une droite. Un vecteur propre associé est le vecteur K de coordonnées 40, 10, 5, 2 et 1, donc L est proportionnel à K, c'est-à-dire qu'il existe un scalaire a tel que L = a K. Ce nombre adépend de l'effectif de la société, qui vaut 5 700, ce qui prouve que a = 100. Les effectifs tendent donc vers a = 4 000, b = 1 000, c = 500, d = 200 et e = 100.

Des chefs en surnombre

La règle établie concernant les promotions dans l'entreprise aboutissent à cette répartition entre les niveaux hiérarchiques. Si elle ne convient pas, il suffit de modifier la règle concernant les promotions internes, c'est-à-dire la matrice de transition A, jusqu'à obtenir un résultat convenable à la politique souhaitée. Par exemple, si on modifie les départs à l'extérieur des échelons B, D et E en respectivement 20 %, 20 % et 30 %, la matrice de transition A devient :

\( A_{\textrm{nouveau}}=\begin{pmatrix} 0,9 & 0,1 & 0 & 0 & 0 \\ 0,2 & 0,7 & 0,1 & 0 & 0 \\ 0 & 0 & 0,8 & 0,2 & 0 \\ 0,2 & 0 & 0 & 0,6 & 0,2 \\ 0,3 & 0 & 0 & 0 & 0,7 \\ \end{pmatrix}. \)

Le vecteur propre K devient le vecteur de coordonnées 326, 12, 6, 3 et 2, ce qui double pratiquement l'effectif du niveau hiérarchique supérieur ! Pour un effectif constant, on obtient entre 192 et 193 personnes à l'échelon E. En diminuant les départs vers l'extérieur, on obtient donc des chefs en surnombre et peu d'exécutants. Pour décrire ce syndrome, en France, on a coutume de parler d'armée mexicaine, ce qui fait référence à une époque révolue, celle de Pancho Villa, dont la légende dit que cette armée comprenait (presque) plus de colonels que de soldats…

En simulant un millier de fonctions dans l'entreprise, on peut également évaluer la longueur moyenne d'une carrière en suivant le schéma donné. On trouve un peu plus de neuf ans. On peut également évaluer les coûts en tenant compte des indemnités éventuelles pour ceux qui quittent l'entreprise, et donc chercher à les minimiser.

La propriété de A concernant la limite de X_n se généralise aux matrices, dites stochastiques régulières, dont tous les éléments sont positifs, les sommes des lignes toutes égales à 1 et possédant une puissance dont tous les éléments sont strictement positifs (dans le cas de la matrice A, A4 vérifie cette propriété). Il s'agit du théorème de Perron–Frobenius, un fleuron de l'algèbre linéaire.