Un modèle économique est une description simplifiée, abstraite, théorique, permettant la représentation et l'étude d'un système économique réel global ou plus limité (secteur, problématique, entreprise). Il permet, outre une simple description, de réaliser des prévisions et simulations, voire de réaliser des optimisations. Dans ce cas, il peut être utilisé par les décideurs économiques ou politiques pour justifier certaines prises de position stratégiques dans les entreprises et certaines décisions économiques générales. Il peut aller jusqu'à justifier la planification et l'allocation de ressources.

Les modèles très généraux et complexes sont établis par des organismes spécialisés, comme l'Insee en France ou le Bureau fédéral du plan en Belgique. Ces entités ont pour missions la tenue de statistiques, d'indices et d'indicateurs économiques, sociaux et environnementaux, la réalisation d'enquêtes auprès des entreprises et des ménages, l'élaboration de modèles permettant de réaliser des prévisions et projections et d'évaluer l'efficacité socio-économique des politiques menées ou envisagées. Pour cela, elles doivent gérer des bases de données colossales. Les domaines où elles exercent leur activité sont variés : économie régionale, nationale et internationale, marché du travail, finances publiques, protection sociale et secteur de la santé, démographie, transport, mobilité et énergie…

Se confronter à la réalité 

Une loi économique est généralement représentée par des équations liant les variables économiques faisant l'objet de la modélisation ; ces équations traduisent un comportement économique théorique et font intervenir les variables qui sont susceptibles d'influencer les variables d'intérêt. Certaines équations d'un modèle sont de simples identités (définition de concepts ou équations de la comptabilité nationale par exemple), d'autres expriment une simple tendance (évolution dans le temps). Les plus intéressantes sont des équations fonctionnelles, qui font intervenir les variables économiques mais dépendent également de paramètres qu'il convient d'estimer à partir des observations (données historiques). Elles peuvent être d'ordre technique, comme une fonction de production, ou d'ordre comportemental, comme la loi de la demande ou une fonction de consommation. Dans le cadre d'une utilisation pour une prise de décision, certaines variables (niveau de taxation, taux directeurs…) ne sont pas mesurées, mais sont à la disposition du décideur politique ou économique, qui peut alors effectuer un certain nombre de simulations préalables.

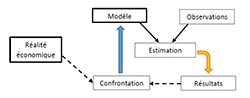
L'économétrie est un ensemble d'outils quantitatifs qui permettent, sur base des observations, d'estimer les paramètres d'un modèle, mais également d'en tester la validité. Du modèle estimé, on peut déduire un certain nombre de résultats ; la confrontation de ceux-ci avec la réalité du terrain permet la validation (ou non) du modèle. En cas de désaccord, le modèle doit être adapté. Et ainsi de suite… jusqu'à sa stabilisation.

Les modèles ne sont qu'une représentation simplifiée de la réalité : les relations d'interdépendance des variables économiques ne peuvent jamais être toutes prises en considération. Les variables, concepts et résultats économiques n'ont pas la même fiabilité que ceux que l'on observe dans les sciences comme la physique ou la chimie : un modèle économique est tributaire non seulement des données qui le nourrissent, mais également de la subjectivité de l'économiste qui le conçoit. La science économique est si complexe que sa modélisation est un art bien difficile. Même les modèles qui ont fait preuve de réelles qualités doivent toujours et encore être remis sur le métier. Enfin, l'interprétation des résultats issus d'un modèle demande une grande expérience et une connaissance fine des mécanismes économiques.

Dans un modèle à une seule équation, une variable Y est privilégiée, la variable dépendante, encore qualifiée d'endogène. C'est elle qui est expliquée par les autres variables X₁, X₂… X_k du modèle, dites variables indépendantes ou exogènes. La variable dépendante est liée aux variables indépendantes par une relation fonctionnelle Y = f (X₁, X₂… X_k, a₁, a₂… a_p) qui fait intervenir des paramètres inconnus, a₁, a₂… a_p. Cette relation porte le nom d'équation de régression. L'estimation de ces paramètres sur base des observations de l'ensemble des variables X₁, X₂… X_k et Y n'est aisée à réaliser de manière analytique que si la relation est linéaire en les paramètres : Y = a₀ + a₁X₁ + a₂X₂ + … + a_kX_k. Pour les cas plus généraux, des méthodes numériques itératives sont indispensables.

Dans certains modèles, toutes les variables sont considérées à une même époque t. On parle alors de modèle statique. Si des époques différentes interviennent (t, t – 1, t – 2…), on parle de modèle dynamique, qui traduit un enchaînement des variables dans le temps. Les variables considérées en t sont qualifiées de courantes, les autres sont appelées retardées. Mais un modèle est une approximation de la réalité : les variables X₁, X₂… X_k ne suffisent pas à expliquer complètement la variable Y. Il existe donc un écart Ɛ appelé résidu entre les deux membres de l'équation ci-dessus. Le modèle de régression linéaire à une seule équation prend la forme définitive :

Y = a₀ + a₁X₁ + a₂X₂ + … + a_kX_k + Ɛ.

Le résidu est une variable aléatoire (comme la variable dépendante Y). La théorie de la régression formule des hypothèses quant à cette variable aléatoire, utiles lorsque l'on souhaite procéder à la validation du modèle. Considérons n observations de chaque variable du modèle, ainsi que les résidus associés. Le critère le plus communément retenu pour estimer les paramètres consiste à minimiser la somme des carrés des résidus selon la méthode des moindres carrés ordinaires. La recherche des paramètres est donc un problème de minimisation d'une fonction des variables a₀, a₁, …, a_k (voir encadré).

De la qualité du modèle

Un indicateur qu'il est intéressant de calculer pour se faire une idée de la qualité d'un modèle est le coefficient de détermination, qui représente la proportion de variance expliquée par le modèle relativement à la variance usuelle. Ce coefficient est toujours compris entre 0 et 1. Une valeur proche de 1 correspond à un modèle de bonne qualité.

Considérons des données relevées par le Bureau of Labor Statistics pour la consommation alimentaire par personne (q), le prix moyen des biens alimentaires (p) et le revenu déflaté (y), c'est-à-dire débarrassé des effets de l'inflation.

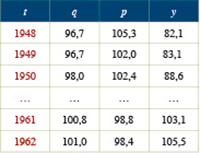
Le modèle proposé par les économistes pour ce genre de données est de type exponentiel. Il n'est pas linéaire en ses paramètres, mais linéarisable par passage aux logarithmes. En transformant les observations par passage aux logarithmes, on arrive au modèle estimé q = 8,94 p^– 0,24 y^0,14, qui explique environ 87 % de la variance de la consommation pour l'alimentation.

Il existe évidemment des modèles plus sophistiqués, à plusieurs équations et plusieurs variables dépendantes. Les équations ne peuvent être traitées individuellement, car non seulement les variables indépendantes sont présentes dans plusieurs équations, mais il en va de même des variables dépendantes. Dans le cadre linéaire, et pour m variables dépendantes et k variables indépendantes, on mettra le modèle sous la forme de m équations du type :

b_i,1Y₁ + … + b_i,mY_m + a_i,1X₁ + … + a_i,kX_k = 0 (i = 1, 2… m).

On introduit un résidu par régression, mais on ne peut utiliser le critère des moindres carrés vu précédemment que si une seule variable endogène est présente par équation (ce qui n'est généralement pas le cas). Le traitement doit alors commencer par la résolution algébrique du système d'équations de manière à se ramener à cette situation. Le problème est ensuite, à partir des éléments estimés, de remonter aux paramètres du modèle de départ. Si cette « opération de retour » est possible de manière unique, le modèle est qualifié d'identifiable et la problématique de l'estimation a été résolue par la méthode des moindres carrés indirects. Si ce n'est pas possible, c'est-à-dire si cette résolution inverse conduit à une impossibilité ou à une indétermination, le modèle est qualifié de sur-identifiable ou de sous-identifiable et d'autres techniques doivent être envisagées, comme la méthode des moindres carrés à deux niveaux.

Vers une description réaliste

Ce n'est là que le début ! De nombreux compléments peuvent être envisagés, selon les situations. En ce qui concerne les hypothèses affectant les résidus, par exemple, il convient de mettre en place des tests afin de les valider ou de les infirmer et, dans ce second cas, d'élaborer des méthodologies pour redresser les données ou le modèle afin qu'elle soient satisfaites. Pour ce qui est de la sélection des variables explicatives, on observe que celles-ci sont généralement trop nombreuses. Il convient alors d'utiliser un coefficient de détermination ajusté pour évaluer la qualité du modèle (car plus on ajoute de variables indépendantes, plus le coefficient de détermination usuel s'améliore, artificiellement) et de mettre au point des méthodologies de sélection pas à pas des variables exogènes intéressantes. Enfin, face à certaines particularités, comme la non-linéarité ou la présence de périodes d'observations atypiques (comme les années de guerre), on peut introduire des variables indicatrices, et une estimation du retard idéal à proposer dans les modèles dynamiques. Plus on a d'informations, de mesures, plus on a d'exigences pour le modèle descriptif. Mais plus ce modèle se révèle complexe ! C'est le prix à payer pour une description réaliste du monde économique.