Le dictionnaire de la langue française peut être vu comme un ensemble fini de mots composés de lettres (majuscules, minuscules, accentuées). Les instructions d'un langage de programmation sont spécifiées dans le manuel d'utilisation et sont en nombre fini. Par contre, les noms de variables ou de fonctions qu'un programme informatique peut manipuler sont en nombre potentiellement infini. Les séquences génétiques sont des mots (souvent très longs) composés de caractères de l'ensemble {A, C, G, T} des quatre nucléotides. Un point commun à tous ces domaines est la notion de langage.
L'alphabet : le b.a.-ba
Pour écrire des mots, il faut un alphabet (un ensemble fini de caractères). Un mot est une suite finie de caractères d'un alphabet donné. Par exemple, avec l'alphabet {a, b, c}, il est possible de composer les mots bbca, aaa, bcbcbc, acbc…
Un langage (abstrait) L d'alphabet A est simplement un ensemble (fini ou infini) de mots composés de caractères de A. Il est ainsi possible de manipuler par exemple le langage (infini) de tous les mots sur l'alphabet {a, b} composés d'un nombre impair de a : {a, aaa, aaaaa… ba, ab, abaa, baaa, babbaa…}. Cette définition abstraite capture les caractéristiques des situations informatiques, biologiques, linguistiques évoquées plus haut, et bien d'autres.
Afin de manipuler automatiquement un langage L, il est essentiel d'avoir un mécanisme qui prend en entrée un mot et qui « dit » si ce mot fait, ou non, partie de L. Les automates finis déterministes (AFD) ont justement été créés pour ça ! Un tel objet M est la donnée de plusieurs éléments. Tout d'abord, un alphabet A. Ensuite, un ensemble fini d' états, Q = {q0, q1… qk}. Dans cet ensemble, on distingue q0, l' état initial de M. C'est la « porte d'entrée » de M. On distingue aussi le sous-ensemble F de Q des états accepteurs de M. Un mot w = x1 x2… xn traité par M est initialement écrit sur le ruban de M (c'est la mémoire d'entrée, en lecture seule). Chaque caractère xi de w occupe une case du ruban. Une tête de lecture de l'automate pointe, au départ, sur le premier caractère, x1, de w.
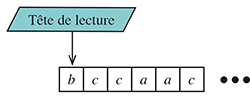
Le dernier élément indispensable de M est sa fonction de transition d, qui va permettre de le « piloter ». La fonction ẟ possède deux arguments : le caractère x lu par la tête de lecture sur le ruban et l'état p dans lequel est M (au début, x = x1 et p = q0). Dans cette configuration, ẟ(p, x) = q est l'état dans lequel passe M après avoir traité le caractère x, lu par la tête de lecture (il n'est pas interdit d'avoir p = q). La tête de lecture se déplace ensuite d'une case sur la droite.
Ces deux opérations constituent une transition de M (d'où le nom de la fonction ẟ).
Un point important dans la définition de M est que, pour tout état p de Q et pour tout caractère x de A, il existe un unique état q de Q tel que ẟ(p, x) = q. Cette caractéristique est l'aspect « déterministe » de l'AFD.
Un exemple d'AFD est donné ci-dessous. Dans le schéma, un état est représenté par un sommet d'un graphe. Une transition d'un état p vers un état q est représentée par un arc de p vers q. Le caractère x présent sur la flèche est le caractère sur lequel se fait la transition. Cette flèche étiquetée représente donc ẟ(p, x) = q. Ici, ẟ(q0, b) = q1, ẟ(q1, a) = q3, ẟ(q1, b) = q3… Un état accepteur est représenté par un sommet entouré de deux cercles (comme q1 et q3).
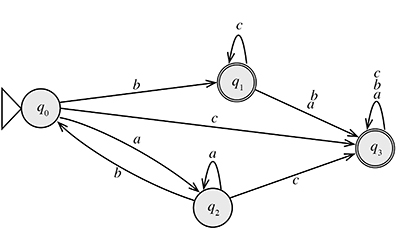
Que faire avec une si belle machine ? Jouons avec ! Traitons le mot w1 = aabab. Il suffit de partir de q0 puis de suivre les flèches, en lisant les lettres du mot, une à une. On obtient la suite q0 (a) – q2 (a) – q2 (b) – q0 (a) – q2 (b) – q0. À la fin du traitement du dernier caractère du mot w1, l'automate est dans l'état q0, ce que l'on écrit ẟ*(q0, w1) = q0.
Traitons un autre mot : w2 = bcca. Ici, ẟ*(q0, w2) = q3. La différence entre les deux est que le traitement de l'un (w1) se termine sur un état non accepteur (q0) et l'autre (w2) sur un état accepteur (q3). Le mot w1 est dit refusé alors que w2 est accepté par M. L'ensemble des mots acceptés par M est le langage de M, noté L(M). Le langage accepté par l'AFD précédent contient donc w2 mais pas w1.
Un autre automate qui accepte tous les mots sur l'alphabet {a, b} contenant un nombre impair de a (et un nombre quelconque de b), comme a, aaa, aabba, abbbaba, bbabaa…, serait le suivant.
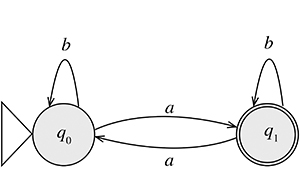
Un AFD peut être mis en œuvre sur un système informatique embarqué à capacités limitées : il suffit de suivre les flèches.
Quand le langage s'échappe
Étant donné un automate fini déterministe M, il existe donc un (unique) langage accepté par M qui est, par construction, L (M). Mais la « réciproque » est-elle vraie ? Est-ce-que, pour tout langage L, il existe un AFD M acceptant L (tel que L (M) = L) ? Réfléchissez-y quelques instants…
Si la réponse était oui, tout langage pourrait être manipulé de manière efficace, mécanique, et non ambiguë. Ce serait vraiment très pratique ! Mais la réponse est… non. Certains langages ne sont acceptés par aucun AFD. Par exemple, le langage sur l'alphabet {a, b} contenant, pour tout entier k, le mot composé de k caractères a suivis de k caractères b, contient des mots comme ab, aabb, aaabbb, aaaabbbb… Pourtant très simple à décrire, il est hors de portée d'un AFD ! La raison profonde provient du fait qu'il est impossible, avec un nombre fini d'états, de mémoriser le nombre de a lus, pour le comparer ensuite au nombre de b. Cela peut être prouvé mathématiquement. D'autres types d'automates, munis d'une mémoire, acceptent ce langage. Mais ces automates ont eux aussi des langages qui leur échappent…
Au sommet de la pyramide des automates les plus perfectionnés se trouvent les machines de Turing. L'intérêt de ces dernières est essentiellement théorique ; elles permettent de définir la notion de calculabilité, mais cela est une autre (et très vaste) histoire.