Une information mathématique est véhiculée par la parole ou par un texte. Dans la plupart des classes de mathématiques, elle est vocale, car il s'agit d'expliquer et de s'expliquer. Quant aux textes eux-mêmes, ils sont composés de mots et de signes, dont la disposition sur la feuille de papier ou à l'écran correspond à des significations précises. Ce sont des écritures. Les mots et certains signes sont prononçables, mais l'énonciation d'un texte est parfois difficile en raison des embarras pour dire ces dispositions. Parfois, il est plus aisé de simplement regarder. Aussi, considérer les mathématiques du seul point de vue de leurs « langages » risque de gommer ou d'ajouter des difficultés. Les mathématiques se disent, elles se voient aussi.
Les jeux entre parole et regard
La part de la parole et du regard a changé dans l'histoire des mathématiques, ainsi que la manière dont la parole et le regard s'articulent. Autrement dit, les jeux entre parole et regard font partie des mathématiques. Confrontons à cet égard cinq textes historiques, à dire et à voir.
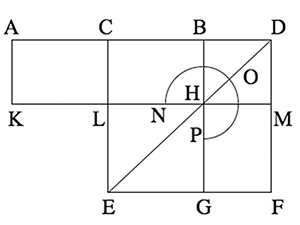
Dans le Livre II des Éléments d'Euclide (traduit par Bernard Vitrac), la proposition 6 procède, comme toutes les autres, en étapes bien précises. La première est une longue phrase composée de mots.
« Si une ligne droite est coupée en deux parties égales et qu'une certaine droite lui soit ajoutée en alignement, le rectangle contenu par la droite entière plus la droite ajoutée et la droite ajoutée, est, pris avec le carré sur sa moitié, égal au carré sur la droite composée de sa moitié et de la droite ajoutée. »
Ici, « ligne » désigne un segment. Les mots « droite », « rectangle » et « carré » ont été définis, les autres font partie du vocabulaire très restreint d'Euclide ; ils prendront un sens dans la suite du traité. La deuxième étape est une phrase composée de mots et de lettres.
« En effet, qu'une certaine droite AB soit coupée en deux parties égales au point C, et qu'une certaine droite BD, lui soit ajoutée en alignement. Je dis que le rectangle contenu par AD, BD, pris avec le carré sur CB, est égal au carré sur CD. »
Les lettres A, B, C et D sont ce que nous appelons des indices : elles servent à « indiquer » des points, en particulier des extrémités de segments. La phrase invite donc à regarder un segment [AB] coupé en son milieu C et un segment [BD] aligné avec A et B. L'expression « carré sur CB » désigne une surface carrée construite sur [CB], et non pas le carré d'une longueur. Le terme traduit par « ajoutée » ne correspond pas à une addition de longueur, mais à une disposition géométrique. La troisième étape est la construction d'une figure, par intersection de droites et de cercles (les instruments ne sont pas mentionnés dans le texte euclidien). Elle utilise des constructions déjà établies (milieu, parallèle, carré).
« En effet, que le carré CEFD soit décrit sur CD. Et que DE soit jointe ; et, d'une part que par le point B soit menée BG parallèle à l'une ou l'autre des droites EC, DF ; et d'autre part que par le point H, soit menée KM parallèle à l'une ou l'autre des droites AB, EF ; et que par le point A, soit encore menée AK parallèle à l'une ou l'autre des droites CL, DM. »
Maintenant, les mots de la phrase initiale correspondent à une disposition spatiale de signes et de figures sur la feuille. La figure complète efface le chemin de la construction, mais elle sert à la quatrième étape, celle de la démonstration. Les rectangles sont désignés par deux sommets opposés, ainsi le signe AL est ce que nous appelons symbole, c'est-à-dire une convention pour parler du rectangle. De même, NOP est un symbole pour désigner le gnomon en forme d'équerre.
« Or, puisque AC est égale à CB, AL est aussi égal à CH (I, 36). Mais CH est égal à HF (I, 43), et donc AL est égal à HF. Que CM soit ajouté de part et d'autre. AM tout entier est donc égal au gnomon NOP. Mais AM est le rectangle contenu par AD, DB car DM est égal à DB, et donc le gnomon NOP est égal au rectangle contenu par AD, DB. Que LG – qui est égal au carré sur BC – soit ajouté de part et d'autre. Le rectangle contenu par AD, DB, avec le carré sur CB, est donc égal au gnomon NOP avec LG. »
Les mots « puisque » et « donc » indiquent que le texte fournit un raisonnement déductif, tandis que « mais » invite à regarder les parties de la figure sur lesquelles s'appuie le raisonnement. Chaque partie du texte euclidien correspond à une nouvelle étape dans l'usage particulier de mots et de signes – indices ou symboles – qui sont tous prononçables. Le nombre de mots est limité et les structures des phrases très stéréotypées : ce sont deux caractéristiques qui aident à mieux saisir l'enchaînement du raisonnement. Dans son Cours mathématique de 1644, Pierre Hérigone accentue cet effet avec un texte contenant des signes, lettres ou symboles (voir en encadré).
Hérigone met en évidence les différentes étapes de la proposition, nommées par lui « hypothèse », « requis », « préparation », « démonstration », car « la distinction de la proposition en ses membres soulage aussi la mémoire, et sert grandement à l'intelligence de la démonstration ». Il a supprimé certains mots du texte euclidien qui seraient toujours présents à l'oral ; par exemple, la dernière ligne se dit « rectangle adb ajouté au carré cd égale carré cb » (voir en encadré le texte de Pierre Hérigone). Les conjonctions « puisque » ou « donc » qui articulent le raisonnement sont aussi supprimées, mais les numéros désignant des axiomes ou des propositions, sur lesquels s'appuie chaque affirmation, sont en marge. À l'oral, il faudra dire par exemple, « d'après la proposition ». Finalement, les qualités que Hérigone revendique pour son texte s'accordent avec une de ses acceptions : c'est un texte à regarder. Mais il est possible aussi de le lire en disant tout.
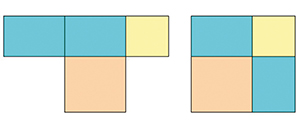
Cela est très différent avec un « texte à la chinoise », où les couleurs sont des codes pour désigner des figures égales (superposables). Le seul mot qui pourrait être ajouté est « Regarde ! », car l'énoncé et sa preuve sont données en même temps. Le lecteur n'a pas besoin d'être convaincu par des mots, le seul regard doit lui rendre évident ce qui est suggéré. On peut cependant encore imaginer ce qui serait dit à un lecteur qui ne serait pas versé dans la géométrie. L'explication orale ou écrite décrirait un puzzle de quatre pièces et le déplacement de l'une des pièces. C'est à la fois très proche du ressort de la démonstration euclidienne, et très éloigné de son esprit.
L'arithmétisation de la géométrie
En 1637, René Descartes s'oppose à la géométrie des Anciens en présentant une « méthode » pour « résoudre tous les problèmes de géométrie ». À cet effet, il introduit un segment unité, qui permet d'étendre les opérations de l'arithmétique (addition, soustraction, multiplication, division et racine carrée) des nombres aux segments. Ainsi, dans la géométrie cartésienne, il n'y a plus à considérer que des segments. En particulier, l'aire d'un rectangle est associée à la multiplication de ses côtés. Alors, pour résoudre un problème, il faut donner des noms à tous les segments qui interviennent : a, b, c, d… pour les segments connus, x, y, z… pour les segments inconnus. L'énoncé d'un problème est traduit par des équations algébriques, qu'il ne reste plus qu'à résoudre. La résolution d'un problème demande de regarder non des figures, mais des équations. Ici, les lettres désignent non des points, mais des segments.
Bernard Lamy est un cartésien qui adopte les idées d'Arnauld (voir en encadré) dans les Éléments de géométrie ou de la mesure du corps de 1695. La proposition 6 est dans la partie consacrée au Livre II d'Euclide. Ici, les lettres désignent les segments : z est le segment coupé en deux et b est celui qui lui est ajouté. Alors il faut montrer que (z + d) d + bb = (b + d)(b + d). Le signe pour l'égalité est désormais standard, mais les exposants pour le carré d'une longueur font toujours défaut.

Le texte de Bernard Lamy.
Le texte utilise les opérations et les mots de l'algèbre, auxquels se mêlent les mots « ainsi », « car », « or », « donc », exprimant un raisonnement déductif. Le texte reste donc lisible à l'oral, mais il vaut mieux regarder les équations plutôt que les ânonner. Il n'est accompagné d'aucune figure, ce que Lamy revendique dans les « éclaircissements » situés en fin de l'ouvrage.
« Ces dix propositions d'Euclide seraient sans doute plus évidentes si je les avais accompagnées de figures ; mais outre qu'il est facile de les faire […] j'ai cru qu'il était bon de s'accoutumer à concevoir ces sortes de vérités sans se représenter des figures. Elles ne sont point nécessaires ; car pour comprendre que le carré b + d est égal aux quarrés de ses parties, savoir à bb et à dd, plus deux fois le plan de ses parties, c'est-à-dire à 2 bd ; il suffit que je conçoive b + d multipliée par b + d produit bb + 2 bd + dd, où je vois aussi évidemment et aussi sensiblement que dans une figure ce qu'il fallait prouver. »

Le texte de Giusto Bellavitis.
Dans le texte de Lamy, le produit de deux lettres correspond à l'aire d'un carré ou d'un rectangle. Mais il n'en est plus de même en 1854 dans Exposition de la méthode des équipollences de Giusto Bellavitis, qui a précédé historiquement la méthode vectorielle. Le mathématicien italien y introduit des opérations de produit et de division de deux segments selon leurs inclinaisons et il énonce les « règles relatives aux grandeurs et aux inclinaisons ». Selon la première, pour trois points A, B, C du plan, on a toujours AB + BC
Bellavitis énonce ainsi « le théorème général » de la méthode :
« Toute propriété des points d'une droite donne un théorème relatif aux points d'un plan, par le seul changement des équations en équipollences. »
Il prend pour exemple la formule de la proposition 6 du Livre II, qui concerne quatre points alignés A, B, C, D, où C est le milieu de [BD], et elle affirme que AB × AD + BC2 = AC2. Bellavitis vérifie, en utilisant la Règle I, que cette égalité peut aussi se lire comme une équipollence exacte avec A, B, C et D quatre points du plan, C étant toujours milieu de [BD] : AB × AD + BC2
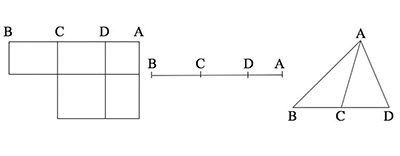
Le premier corollaire examine ensuite le cas particulier où l'angle est droit. Bellavitis remarque que l'équipollence devient AB2 = AC2 + CB2, c'est-à-dire que le corollaire établit… le théorème de Pythagore ! Le passage de la figure de la proposition 6 d'Euclide à celle du théorème de Bellavitis passe par une mise en ligne de l'énoncé, qui a été obtenue algébriquement grâce à la géométrie initiée par Descartes (voir encadré).