Les pièges des taux

 Pour ne pas tomber dans les pièges des pourcentages, il est essentiel de suivre les calculs méticuleusement. Si l'on ajoute 10 % à une somme de 100 €, on lui ajoute 10 € et on obtient 110 €. C'est cela qui importe et non pas le taux. La règle des pourcentages est multiplicative et non additive. Quand on ajoute 10 % à une somme, on la multiplie par 1,1. Si l'on ajoute 10 % à nouveau, on multiplie la nouvelle somme par 1,1. On a donc multiplié l'ancienne par 1,1². Or, 1,1² n'est pas égal à 1,2 mais à 1,21. Ainsi, si l'on ajoute deux fois 10%, on n'ajoute pas 20% mais 21%. De même, une réduction de 20% sur un prix revient à le multiplier par 0,8. Une réduction supplémentaire des mêmes 20% aboutit à une nouvelle application du même taux. Finalement, le prix initial est multiplié par 0,8², soit 0,64, ce qui correspond à un taux de réduction de 36 %, et non de 40 %. Les taux ne s'additionnent pas, ils se multiplient ! En mathématiques, le langage courant peut être source de confusions : s'il est légitime de dire que l'on ajoute un taux à un autre, cela ne signifie pas que l'opération mathématique correspondante soit l'addition. Parfois, ajouter peut signifier multiplier !

Le même phénomène se produit si l'on désire retrouver le prix initial après une réduction. Prenons un exemple qui se produit dans des expositions de peintures privées. N'ayant pas d'intermédiaire à payer, l'artiste y consent souvent une réduction d'un tiers sur les prix de vente en galerie. Que cela signifie-t-il sur la commission des galeries ? Prenons l'exemple d'une toile vendue 1 200 € en galerie, le peintre la vend en direct un tiers (donc 400 €) de moins, soit 800 €. Pour monter de 800 à 1 200, le taux est de 1 200 divisé par 800, soit 1,5. La commission de la galerie est donc de 50% (!).

L'explication est du même ordre que précédemment. En appliquant une réduction d'un tiers, on multiplie le prix initial par 2 / 3. Pour le retrouver, il faut multiplier le final par l'inverse de 2 / 3, soit 3 / 2, d'où nos 50% d'augmentation.

Combien coûte un emprunt

Les questions de pourcentages réservent ainsi bien des surprises. Examinons le résultat de deux réductions consécutives de 2%. Cela ne fait pas 4%, ni 3,6% comme nos calculs antérieurs pourraient le faire penser, mais 3,96%. Pourquoi ? Le calcul est toujours le même : on multiplie deux fois le prix par 0,98. Ce nombre multiplié par lui-même fait 0,9604, d'où le résultat annoncé : dans ce cas, deux et deux ne font pas quatre, mais 3,96…

Certains organismes financiers proposent une somme d'argent appelée réserve de crédit. L'emprunteur choisit lui-même la somme fixe qu'il rembourse chaque mois, les intérêts portent sur la somme qu'il reste à payer, au taux prévu. Imaginons qu'un client décide d'emprunter 1 500 € et d'accepter un prélèvement de 100 € par mois à partir du mois suivant. Le taux d'intérêt mensuel est de 1,5%. Combien de temps le client mettra-t-il à rembourser ? Combien aura-t-il payé à la fin ? Pour le trouver, on construit un tableau permettant de suivre les mouvements d'argent. Chaque mois, on note la dette initiale, l'intérêt, le remboursement et la dette finale, qui est la dette initiale du mois suivant. L'intérêt du mois est toujours égal à la dette initiale multipliée par le taux d'intérêt. En revanche, la dette finale est égale à la dette initiale majorée de l'intérêt du mois moins le remboursement, qui porte ainsi mal son nom !

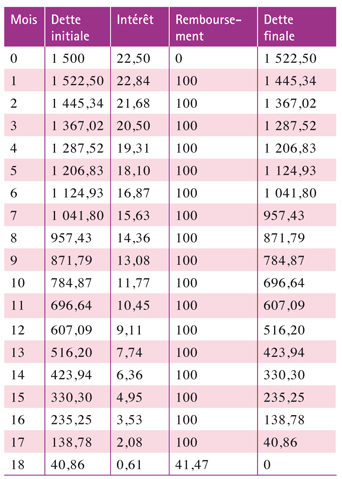L'emprunt est remboursé à la fin du dix-huitième mois de remboursement suivant l'obtention des fonds. Le client aura réglé 1 741,47 € en tout, dont 241,47 € d'intérêts. Établissons une formule mathématique permettant de suivre la suite des dettes à la fin de chaque période. Supposons que le capital emprunté est égal à C, le taux d'intérêt périodique (mensuel ici) t, la mensualité m. Le capital C_i restant dû au début de la mensualité numéro i est égal au capital de la période précédente augmenté de l'intérêt C_i–1 t, duquel on retranche le remboursement m, d'où la relation C_i = C_i–1 (1+t) – m.

On en déduit : 

\( $$C_{i}=C(1+t)^i-m\dfrac{(1+t)^i-1}{t}.$$\\\)

Le nombre de mensualités n est donné par la condition C_n = 0, qui se simplifie en

  \( $$(1+t)^n=\dfrac{m}{m-Ct}.$$\\\)

En passant au logarithme, on obtient n. Dans le cas précédent, C = 1500, m = 100 et t = 0,015 ; on trouve n = 17,12. Il faut donc bien dix-huit mensualités.

Ces calculs permettent de traiter le cas de l'amortissement d'un emprunt par un nombre n fixé d'annuités constantes. La condition C_n = 0 se simplifie toujours en 

\( $$(1+t)^n=\dfrac{m}{m-Ct}$$\\\)  

ce qui permet d'établir la formule donnant la mensualité constante m permettant de rembourser un capital C en n mensualités si le taux d'intérêt est 

t : \( $$m=\dfrac{Ct}{1-(1+t)^{-n}}$$\\\) .

Cette mensualité tient compte d'un remboursement de capital et de l'intérêt sur le capital restant dû. Prenons donc un emprunt d'un capital de 200 000 € sur dix ans au taux annuel de 4%. L'annuité est de 

\( $$\dfrac{{200 000} \times{0,04}}{1-{1,04}^{-10}}={24 658,19} \text{ \euro} $$\\\)

À partir de là, on peut construire le tableau d'amortissement.

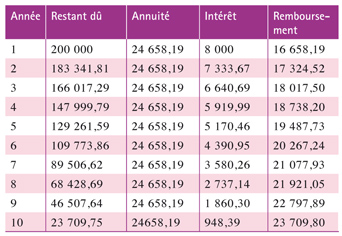Les questions de taux génèrent bien d'autres calculs en mathématiques financières ; ils répondent tous au même type de raisonnement. Ne vous faites plus piéger !