On retrouve dès l'Antiquité des indications chiffrées ramenant l'effectif total à 100. Cela permet plus aisément de comparer différentes situations qu'avec des effectifs différents. L'empereur Auguste introduisit par exemple un impôt de 1% sur les ventes d'objets de consommation, connu sous le nom de centesima rerum venalium. Il faut cependant attendre la fin du Moyen Âge et l'essor du commerce pour voir leur usage se répandre. Ce n'est pas un hasard si cela correspond aussi à l'extension de l'utilisation des chiffres arabes en Occident. Si le choix de 100 est dû à la numération en base 10, l'appréhension rapide des données est facilitée par l'emploi de la numération de position.
Un nom et un symbole
En français, le terme « pour cent » est parfaitement explicite. Ce n'est pas le cas dans d'autres langues, comme l'anglais (avec percent) ou l'allemand (avec Prozent) alors que 100 se dit respectivement hundred et hundert. Cette terminologie apparaît en fait en italien où l'on trouve l'expression per cento dès le XIVe siècle. Cependant, c'est souvent sous sa forme latine per centum qu'on le rencontre à cette époque. On trouve pour la première fois, dans un manuscrit daté de 1425, la notation p.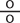
, le p étant l'abréviation de per et les deux petit rond désignant cento. Depuis, le p. a disparu et la barre de fraction est devenue oblique.
Le succès de l'utilisation des pourcentages, désormais courante dans de nombreux domaines, s'explique par la vision claire et rapide qu'elle procure et les comparaisons qu'elle permet : 51% des naissances sont des garçons, 60% des reçus au bac sont des filles, 22% des électeurs ont voté pour le candidat Lambda. Encore faut-il savoir les manier : le principal problème est de comprendre quelle est la référence et se méfier lorsqu'elle varie. Trop souvent on confond « 80% d'une classe d'âge obtient le baccalauréat » avec « 80% des candidats ont obtenu le baccalauréat ». Est-il clair pour tous qu'avec une TVA à 20%, celle-ci correspond à 1/6 (soit environ 16,67 %) du prix total ? Lorsque le taux de chômage passe de 10% à 8%, ceci correspond à une baisse de 20%, et non de 2% comme on l'entend si souvent dire. Est-il clair aussi que les expressions « les deux quantités diffèrent de 20% » ou « l'écart entre les deux valeurs est de 20% » n'ont pas de sens, puisqu'on ignore laquelle est la référence et celle qu'on lui compare ? Autant dire que les pièges sont multiples.
Illustrons le piège des pourcentages sur un simple petit exemple comme les journaux nous en relaient quotidiennement. Un homme politique a proposé la mesure suivante s'il revenait au pouvoir : « 30% d'heures en plus pour les enseignants, 30% de rémunération en plus pour les enseignants et 30% d'enseignants en moins. »
Que peut-on conclure de cette proposition ? Ceci permettra-t-il d'assurer autant d'heures de cours ? Devra-t-on faire varier le nombre d'élèves par classe si l'on maintient le nombre d'heures de cours pour chacun d'entre eux ?
L'effectif du corps professoral sera multiplié par 0,7 mais chaque enseignant multipliera le nombre d'heures de cours effectué par 1,3, ce qui donnera un nombre d'heure de cours multiplié par 0,7 x 1,3 = 0,91. Il y aura donc une baisse des cours assurés de 9%. Pour maintenir l'horaire de chaque élève, une seule solution, augmenter le nombre d'élèves par classe ; mais de combien ? Il faut diminuer de 9% le nombre de classes, donc, pour que tout élève soit scolarisé, il faut que chaque classe multiplie son effectif par 100 / 91= 1,0989… soit une augmentation de près de 10% (9,89% pour être plus précis).
Si l'on avait voulu conserver le nombre d'élèves par classe en augmentant de 30% l'horaire des enseignants, il aurait fallu diminuer le corps professoral de 30 / 130 = 0,2308, soit d'environ 23%, et déclarer « 30 % d'heures en plus, 30% de rémunération en plus et 23% d'enseignants en moins ». Certes, le message aurait été moins clair mais tellement plus correct !
Pourcentages et augmentations
L'utilisation des pourcentages pour indiquer des variations apparaît, elle aussi, dès la fin du Moyen Âge en lien avec le développement du commerce et celui, parallèle, des banques. L'objet est en fait différent du pourcentage considéré comme partie d'un tout. Son maniement prête à l'erreur car on a tendance à manier le taux de variation et non la quantité obtenue. Ainsi, une augmentation de 20% correspond à passer de 100 à 120. Une nouvelle augmentation du même taux amène à 120 x 1,2 = 144, donc à une variation de 44% (et non 40% comme on l'entend trop souvent). Cette erreur consiste à additionner les taux et non multiplier par ce taux augmenté d'une unité. La formule du binôme nous montre l'erreur :
Cette erreur correspond à assimiler (1 + x)n et 1 + nx. Si n et x sont « petits », cette approximation est légitime ; par exemple, une augmentation de 2% pendant trois ans donne 6,12 % d'augmentation, ce qui est fort proche des 6% obtenus en additionnant les pourcentages. En revanche, pour n et x très grands, et même seulement « plutôt grands », le résultat devient tout à fait faux. Pour n = 8 et x = 10, on obtient par exemple 114,36% d'augmentation, très loin des 80% que fournit l'approximation.
En réalité, le pourcentage est le quotient de deux quantités de même nature ; il n'a donc pas d'unité et, de ce fait, c'est un nombre pur. Mathématiquement, 83% est une notation commode et parlante du nombre 0,83. Bien manié, il permet des comparaisons faciles, mais sa mauvaise utilisation est si courante que son utilisation devrait être réduite chaque fois qu'une exposition plus simple peut être utilisée, surtout à l'attention du grand public.