Dans l'Antiquité, les architectes des monuments de grande envergure étaient aussi des mathématiciens. Il leur fallait en effet des connaissances en géométrie comme en arithmétique pour agencer leurs bâtiments. Les pyramides d'Égypte en sont un exemple ; elles sont des volumes simples avec des symétries. De plus, il semble que l'on retrouve dans les mesures de leurs éléments des relations avec les nombres pour des raisons plus mystiques que rationnelles. On sait combien le nombre d'or se retrouve dans différentes constructions antiques…

Mystique et mathématiques

 Brillants mathématiciens, les Grecs sont aussi de grands architectes. La construction des temples révèle une bonne connaissance de la géométrie et le plus célèbre d'entre eux, le Parthénon, situé sur l'Acropole d'Athènes, trouve son élégance dans quelques effets d'optique qui cachent certainement quelques calculs, élaborés pour l'époque.

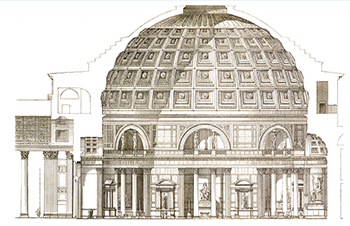Les Romains étaient de grands bâtisseurs, mais de piètres mathématiciens. Au premier siècle de notre ère, Vitruve publie le premier traité sur l'architecture (du moins qui nous soit parvenu). Il y met en avant deux éléments géométriques, la symétrie et les proportions, en fonction de nombres simples. C'est cependant au siècle suivant qu'est édifié à Rome le bâtiment le plus intéressant. Comme son nom l'indique, le Panthéon est dédié à tous les Dieux. Aussi doit-il être une représentation du Cosmos tout en montrant la grandeur de l'Empire romain. L'intérieur est composé d'un dôme semi-circulaire posé sur un cylindre de même diamètre, de telle sorte qu'une sphère peut s'inscrire dans ce volume elle-même s'inscrivant dans un cube. La sphère représente le Cosmos et sa projection circulaire le domaine terrestre et l'Empire romain : symbolisme du monde terrestre se transformant en monde divin. De plus, n'y a-t-il pas caché le problème de la quadrature du cercle ?

À la suite d'une révolte sévèrement réprimée en 532, l'empereur Justinien souhaite bâtir la plus grande et plus belle église au monde dans sa capitale. Il fait appel à deux mathématiciens, Anthémios de Tralles et Isidore de Milet, pour la concevoir. Le premier a découvert quelques propriétés des ellipses et des paraboles et les a utilisées pour fabriquer des miroirs paraboliques concentrant la lumière solaire. Il mourut avant l'achèvement de la basilique en 537. Isidore, quant à lui, enseignait la géométrie à Alexandrie puis à Constantinople. On lui doit aussi une compilation des travaux d'Archimède. L'église des Saints-Serge-et-Bacchus, connue de nos jours sous le nom de Petite Sainte-Sophie (küçük Ayasofia), est aussi l'une de ses œuvres.

La naissance de la perspective

Les bâtisseurs de cathédrales au Moyen Âge ont surtout fait appel à des considérations géométriques afin d'obtenir le plus de stabilité de leurs constructions. On possède malheureusement très peu de renseignements sur leurs méthodes, sinon les carnets de Villard de Honnecourt (XIII^e siècle), qui s'inspire manifestement de l'Antiquité. Ainsi, des pierres trapézoïdales aux angles savamment calculés concourent à la stabilité des édifices. Les arcs-boutants, les ogives et les voûtes sont des éléments construits sur des considérations géométriques. Cependant, les problèmes à résoudre restent élémentaires. Ceci se retrouve aussi dans les ornements : on va de la simple symétrie (que l'on peut admirer dans de nombreux bâtiments) à l'extraordinaire Alhambra, construit par la dynastie nasride à Grenade ; sur ses parois, les motifs géométriques se succèdent de telle sorte que l'on retrouve, dans leur agencement, les dix-sept groupes de pavages.

La Renaissance italienne, bien que s'inspirant de l'Antiquité, innove avec la découverte de la perspective. Les noms de deux grands architectes florentins se détachent, ce sont Filippo Brunelleschi (1377-1446) et Leone Alberti (1404-1472). Le premier est un grand bâtisseur et son chef-d'œuvre est sans doute le dôme de Florence. C'est avant tout un architecte et un homme de chantier. Cependant, il a peint un tableau représentant le baptistère dans lequel il utilise la perspective sans aucune explication. Leone Alberti est un théoricien. On lui doit certes quelques constructions, comme le palais Rucellai à Florence ou le temple des Malatesta à Rimini, mais il reste célèbre pour ses traités sur l'architecture, la peinture, en particulier Della Pittura, dans lequel les principes de la perspective sont pour la première fois énoncés. On y retrouve, avec des graphiques, la notion de point à l'infini, la projection d'un cercle en ellipse et la transformation de carreaux ou de colonnades.

Andrea Palladio publie en 1570 I quattro libro dell'architettura, qui définit les bases de l'architecture de la Renaissance. On y trouve des indications de proportion entre les différentes parties d'un édifice, en particulier sur la taille ou le diamètre des colonnes. Cet ouvrage influencera l'architecture jusqu'au XIX^e siècle.

 
Faire table rase du passé

Le début du XX^e siècle voit l'apparition de mouvements artistiques, brassant tous les domaines, en particulier l'architecture. Ils cherchent à renverser les codes culturels en place et se retrouvent dans des conceptions très pures de leur discipline, privilégiant en peinture et en architecture des formes géométriques simples. Aux Pays-Bas, le mouvement De Stijl (« le style » en néerlandais) est fondé par Theo Van Doesburg en 1917. Piet Mondrian en est certainement le membre le plus célèbre. La revue de même nom prône l'art abstrait et propose une rupture avec le passé. Les architectes les plus célèbres du groupe sont Cornelis Van Eesteren et Gerrit Rietveld ; on doit à ce dernier la Maison Schröder, célèbre pour ses formes géométriques épurées.

En Russie, Vladimir Tatline fonde le constructivisme et publie un manifeste en 1920. Ce mouvement artistique novateur cherche à réagir contre « l'ordre ancien » ; il propose en outre une architecture basée sur des formes géométriques simples comme la droite, le rectangle ou le cercle. En architecture, Vladimir Choukhov en est l'un des membres les plus influents ; il se rend célèbre pour ses constructions « hyperboliques ». Ces mouvements influenceront de grands architectes comme Ludwig Mies van der Rohe, Walter Gropius (fondateur du Bauhaus) et Frank Lloyd Wright.

Cette idée de faire table rase du passé est reprise par des architectes urbanistes qui conçoivent des bâtiments et des cités pour des « hommes nouveaux ». Le Corbusier, le plus célèbre d'entre eux, invente un système de mesure qu'il veut indépendant des conventions humaines. Il le nomme Modulor, mot-valise composé de module et nombre d'or. Très en vogue dans les années 1950, ces démarches sont délaissées voire parfois condamnées par la suite. Ces structures que l'on voulait humaines se sont souvent révélées difficilement vivables.

De nos jours, la place des mathématiques en architecture est de plus en plus importante mais de moins en moins visible. Le travail de conception d'un bâtiment est désormais segmenté ; l'architecte étudie les besoins et les souhaits d'un client. Il fait alors appel à un logiciel de conception des formes qui lui propose différents projets en fonction des paramètres qu'il a introduits. Ce logiciel a bien sûr été créé par des cerveaux humains, mais le projet de l'architecte n'est plus le fruit direct de son imagination : il s'effectue par une habile manipulation de l'outil informatique. Celui-ci est le fruit d'algorithmes savamment élaborés, et leurs auteurs font ainsi partie, eux aussi, de la chaîne de conception des bâtiments, des plus simples aux plus extraordinaires. Bien qu'invisibles, les mathématiques sont donc devenues un outil essentiel de la conception architecturale.