Tangente : Pensez-vous qu'en architecture il soit possible de définir la beauté ?

Depuis Vitruve, les architectes cherchent les mesures et proportions qui conduisent à la perfection, à la beauté. Pour comprendre cette longue quête vers le sublime, peu de maîtres d'œuvres ont décrit leur démarche. Est-il conciliable d'harmoniser mathématiques et beauté ? Les mathématiciens pensent leur science, rigoureuse et mesurable, c'est une approche abstraite qui s'exprime par l'algèbre et la géométrie.

En tant qu'architecte, la géométrie a gravé dans mes réflexions une échelle harmonique qui s'impose dans mes projets. Cela fait référence à l'homme équilibré de Léonard de Vinci, qui reprend le dessin de Vitruve. Le Corbusier, en introduisant le Modulor, participe de cette harmonie qui sert de jalon dans l'élaboration d'un projet.

À gauche : l'homme équilibré de Léonard de Vinci,
à droite : le Modulor est un système de proportions harmoniques imaginé par Le Corbusier, intégrant la section dorée.

Les Éléments d'Euclide, base de notre géométrie, permettent à tout projeteur de se mouvoir dans l'expression architecturale qui impose plans, coupes, élévations. À partir de ces trois expressions, on est en mesure de penser une restitution tridimensionnelle, facilitée aujourd'hui par l'informatique en 3D. Avoir en tête la hauteur d'un siège ou d'une table, la hauteur de vue d'un adulte ou d'un enfant, permet de réaliser des projets adaptés à l'usage voulu par le maître d'ouvrage. Tout au long de ma carrière, cette approche a suffi à assouvir ma recherche d'une esthétique satisfaisante.   

Mesurer le beau

Cette esthétique, peut-on la « mesurer », de manière qualitative ou quantitative ?

C'est une interrogation. Les architectes médiévaux sont de tradition orale. Tout se transmet dans le secret de la loge installée sur le chantier : pas de plans ni de descriptifs, au mieux des comptes présentés au Chapitre, le maître d'ouvrage.
En 1961, au couvent Sainte-Marie de La Tourette, Le Corbusier déclare à propos de « l'espace indicible » : « Lorsqu'une œuvre est à son maximum d'intensité, de proportion, de qualité, d'exécution et de perfection, il se produit un phénomène d'espace indicible. Les lieux se mettent à rayonner, physiquement ils rayonnent. Ils déterminent ce que j'appelle l'espace indicible, c'est-à-dire qui ne dépend pas des dimensions mais de la qualité de perfection : c'est du domaine de l'ineffable. » Cette sensation s'applique parfaitement à Notre-Dame de Chartres, par exemple.

Approche de l'espace indicible par l'esquisse du projet.

Pouvez-vous développer cet exemple ?

Depuis un an, je suis confronté à la cathédrale Notre-Dame de Chartres. Nous devons réaliser l'aménagement des abords et implanter, sous l'esplanade du parvis, un monument culturel qui exalte la ville de Chartres antique et intègre un centre d'interprétation de ce monument historique tout en maintenant un espace qui valorise les missions du monument gothique. Toute conception architecturale doit se confronter aux mémoires de cette magnifique architecture des XII^e et XIII^e siècles, monument historique français inscrit au Patrimoine mondial de l'Unesco. Une des pistes à laquelle je m'intéresse est celle de l'esprit des maîtres d'œuvre qui ont imaginé toutes ces prouesses.
Pour comprendre les approches de leurs travaux, nous disposons de quelques témoignages. Les vitraux, qui sont, pour la plupart, contemporains de la construction au XIII^e siècle, présentent les outils des compagnons. Le carnet de dessins de Villard de Honnecourt reproduit des croquis pris sur le motif lors de la construction de cathédrales, dont celle de Chartres. Les ouvrages de John James, architecte australien, qui s'est dit envouté par cet édifice lors d'une visite en 1969, nous renseignent également : James a entrepris un « travail de bénédictin », cherchant dans cet immense livre de pierres, à travers les pierres elles-mêmes, les traces et l'histoire de ces bâtisseurs. Il mesure tout, au centimètre près, décrit tous les détails de la taille des calcaires et nous permet ainsi une approche mathématique du monument. Dernier élément, enfin, l'École de Chartres, dont l'évêque Fulbert assure la renommée. Il est celui qui pose en 1020 la première pierre de ce qui est encore la crypte de la cathédrale.
Par ailleurs, le fonds très riche de la médiathèque de la Ville et les Archives départementales d'Eure-et-Loir permettent de faire un lien entre écrit et bâti.

Les proportions sur le terrain

Comment se déroulait l'enseignement à l'École de Chartes ?

L'école est un grand centre scientifique du XIIe siècle. On y enseigne les arts du trivium : grammaire, rhétorique et logique. À cette étude des mots il semble que l'école préfère l'étude des choses, l'objet du quadrivium : arithmétique,
géométrie, musique et astronomie. On y étudie Platon et Aristote. Parmi ses chanceliers, signalons Thierry de Chartres, qui écrit dans l'Heptateuque : « La coutume des Anciens était d'apprendre d'abord les mathématiques, afin de pouvoir accéder à la connaissance de la divinité. » L'Heptateuque traite des Éléments d'Euclide et Pythagore. Ce dernier affirmait que « les nombres sont les clés des lois de l'harmonie ». Il y a donc une reconnaissance de la géométrie, dont peut bénéficier le maître d'œuvre de la construction gothique.
 

Il n'y a pas que la géométrie, en architecture. La notion de mesure, plus arithmétique, est essentielle, même dans les questions esthétiques !

John James remarque que la mesure de référence est le « pied du Roi », de 325 mm de long. On trouve cette mesure très ancienne dans la civilisation mycénienne en Crète et dans l'ancienne Égypte. Elle n'a pas varié de plus de 2 mm à travers les âges. Cette unité fait référence, comme le pouce, la paume, l'empan et la coudée, aux dimensions captées sur le corps humain. Le pied est gravé sur les outils, que ce soit sur l'équerre, expression de la matière, ou le compas, expression de l'esprit.
Les mesures de John James sont faites dans un système métrique. Au XIIe siècle, les chiffres sont romains ou depuis peu arabes. Il est essentiel de comprendre l'expression numérique. Le système est décimal, et reste attaché à la référence humaine : les dix doigts sont un boulier commode. La sémiologie numérique impose le « un » comme unité de compte, c'est le doigt… encore un rapport avec le corps.
Sur le chantier gothique règne la corde à douze ou treize nœuds. Sur cette corde, chaque nœud est placé à une coudée de l'autre. L'origine de cet objet est druidique, voire égyptienne. Le système devient duodécimal, plus pratique pour les constructeurs. En formant des segments de trois nœuds, on forme un carré si on relie les extrémités. Avec des segments de quatre nœuds, on obtient un triangle équilatéral ; avec deux nœuds, c'est un hexagone très proche du cercle. Autant de figures simples que l'on retrouve dans la composition architecturale des cathédrales. Il suffit de segmenter la corde en trois parties de trois, quatre et cinq nœuds pour établir un triangle dit « de Pythagore » et tracer un angle droit. C'est à partir de cette corde, de sa capacité à former des surfaces et à servir de compas, que l'on établit le dessin d'un rectangle d'or.

Comment ces mesures très anciennes se sont-elles diffusées en Occident ?

Les écoles, au-delà de l'éducation des clercs, ont une mission de transmission. Elles gèrent la diffusion des écrits et particulièrement celle de la Bible ! Pour produire les parchemins nécessaires à l'édition d'une bible, le bâton du berger doit dénombrer pas moins de sept cents moutons. Sur ces peaux apprêtées, les copistes vont dessiner leurs lettrines ouvragées et accompagner leur calligraphie d'enluminures illustrant des projets oniriques. L'une d'elle, souvent reproduite, célèbre la Jérusalem céleste (voir ci-contre). La Bible est riche en précisions arithmétiques sur les dimensions du temple ou de l'Arche de Noé par exemple. Elle est très précise sur celles de l'Arche d'alliance. Sur quatre côtés, ce sont des rectangles aux proportions d'or, les deux autres extrémités étant des carrés. Ces œuvres écrites et dessinées influencent l'esprit dans lequel les maîtres constructeurs vont œuvrer.

Sciences et symboles

 Le sacré joue donc encore un rôle important à cette époque.

Le 3, le triangle et la trinité ; le 4, le carré et les grands prophètes ; le 7, les jours de la création… Nombre d'ouvrages ésotériques déclinent ces approches, qui tiennent plus d'un roman de Dan Brown que de faits calculés. Il n'empêche que les constructeurs se sont attachés à respecter la magie de chacun des chiffres. Lorsque John James décrit la rosace occidentale, il en trouve le dessin fantastique. Il fait référence au carré solaire magique de 6 × 6. Cette rosace, qui illustre le Jugement dernier, comporte trente-sept ouvertures. C'est le treizième nombre premier ! En le multipliant par la Trinité, on obtient 111, une autre forme de Trinité. Ce carré magique est de trente-six cases. Il est organisé de telle façon que l'addition des chiffres de chaque rang et de la grande diagonale donne 111. Il existe d'autres combinaisons, que l'on peut rechercher selon les axes de symétrie choisis.

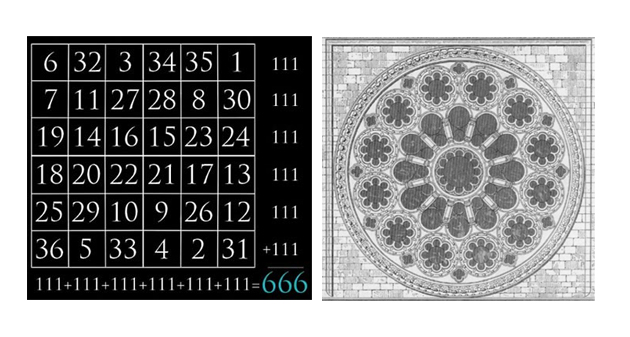
Dans le cadre de notre rosace, il s'agit de trois cercles concentriques inscrits dans un carré. L'ouverture centrale, c'est Jésus-Christ ; au-dessus, en dessous, à gauche et à droite, les quatre évangélistes ; dans les huit autres ouvertures, les autres apôtres. Les douze ouvertures suivantes illustrent la Passion, les anges sonnant trompettes, le Jugement dernier. Douze autres illustrations éclatent la rosace en étoile. Celle-ci, vers l'intérieur, se projette, à 45°, vers le labyrinthe et vers le ciel en direction de la voie lactée. Nous retrouvons les éléments du carré solaire magique.

Quelle est la place des sciences dans un tel contexte ?

Les conditions de lancement d'un projet de cette amplitude obligent des sciences périphériques cachées, peu connues ou disparues. Comme la définition d'un programme, par l'évêque et son chapitre, qui évolue au cours du temps et selon les savoirs des maîtres d'œuvre et compagnons. Ou s'élever très haut vers le ciel du carré tracé au sol vers la voûte céleste. Ou encore se servir de toutes les connaissances en cours pour faire pénétrer intensément la lumière dans l'édifice. Enfin s'ouvrir largement sur la ville et être en capacité d'accueillir le plus grand nombre de citoyens ou de pèlerins venant admirer l'Arche, écrin de reliques attractives. Ça, c'est réel !
Mais il faut disposer de matériaux en mesure de supporter les ambitions du programme. Là aussi, la présence d'une école avec ses compétences géologiques aide à trouver la carrière adéquate. Le calcaire beauceron est de qualité médiocre quant à sa résistance, tout juste bon à assurer les remplissages. À 10 km de Chartres, à Berchères-les-Pierres, une carrière de calcaire lacustre très dense et solide est identifiée. Sur ce territoire, pas de fleuve pour assurer le transport : tout sera transporté par chariots chargeant sept cents tonnes au maximum par trajet. Sans Berchères, pas de Chartres !
Enfin, l'analyse du bâti final révèle une construction irrationnelle. Toutes les structures sont rejetées à l'extérieur pour ménager un immense espace vide.
Cette organisation, au-delà de l'indicible, permet à la lumière d'éclairer l'intérieur du monument. La lumière est sublime, elle éclaire les croisées d'ogive, laissant le sol et la base des colonnes entre ombre et lumière. Cette géométrie minérale savante n'est possible que par le génie des charpentiers, qui ont su disposer leurs échafaudages pour tenir les cintres. L'art des poulies et leviers était précis, chèvres, singes et écureuils illustrent les animations du chantier. La moitié des compagnons étaient charpentiers ou menuisiers. De leurs ouvrages tout est escamoté, ne restent que minces témoignages d'un travail sans lequel rien ne serait. C'est autour de ces jambes de force et poutres que repose la science de la résistance des matériaux et celle de la prouesse que nous admirons. Force des belles mathématiques !