Le nombre d'or fait souvent fantasmer.
Ceux qui se réfèrent au De divina proportione de Luca Pacioli se sont rarement préoccupés du contenu de cet ouvrage, constitué de trois parties : un texte de Pacioli, les illustrations de Léonard de Vinci, et un manuscrit sur les polyèdres de Piero della Francesca. C'est le premier livre imprimé dans lequel l'illustrateur est meilleur que l'auteur. La description du petit rhombicuboctaèdre fournit la première représentation connue de ce polyèdre à la Renaissance. Pourtant, nulle présence du nombre d'or dans ce solide, qui deviendra le symbole de Pacioli. Pacioli obtient ce solide en pratiquant une troncature de son hexahedron abscisus (notrecuboctaèdre). L'objet obtenu possède vingt-six faces. Il donne ensuite le nombre d'arêtes et d'angles solides. « Ce solide est obtenu à partir de l'hexaèdre uniformément coupé [secto], tranché [tagliato] de la même manière sur son pourtour comme montré sur la figure. »
Le problème est que si l'on pratique une troncature sur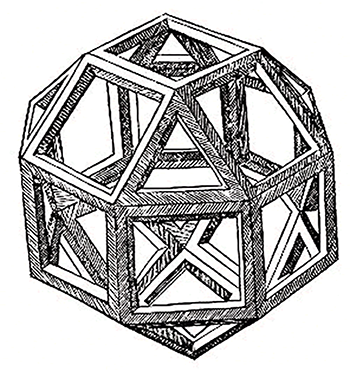 
chaque sommet du cuboctaèdre on n'obtient pas des carrés mais des rectangles ! Il faut ensuite pratiquer une déformation du solide pour transformer les rectangles en carrés. Les auteurs de la Renaissance semblent oublier ce traitement, peu aisé à décrire rigoureusement. Pacioli ajoute en commentaire que ce polyèdre sera particulièrement utile aux architectes, une prophétie qui ne s'est pas vérifiée. Ainsi, si ce texte possède un intérêt historique et artistique évident, sa qualité mathématique laisse à désirer.
Lire la suite
chaque sommet du cuboctaèdre on n'obtient pas des carrés mais des rectangles ! Il faut ensuite pratiquer une déformation du solide pour transformer les rectangles en carrés. Les auteurs de la Renaissance semblent oublier ce traitement, peu aisé à décrire rigoureusement. Pacioli ajoute en commentaire que ce polyèdre sera particulièrement utile aux architectes, une prophétie qui ne s'est pas vérifiée. Ainsi, si ce texte possède un intérêt historique et artistique évident, sa qualité mathématique laisse à désirer.