Les droites de Simson et de Steiner

Le triangle donne lieu a de nombreux alignements spectaculaires : on y déniche la droite de Simson et sa cousine, la droite de Steiner.

S'il est vraisemblable que Robert Simson, mathématicien écossais, connaissait avant Euler, mais sans démonstration, la célèbre droite d'Euler (voir ci-contre), aucun écrit cependant n'atteste qu'il ait trouvé la droite qui porte son nom. La première trace écrite de cette « droite de Simson » date de 1799 et est due… à un autre mathématicien écossais, William Wallace. C'est pourquoi on l'appelle parfois droite de Wallace–Simson.

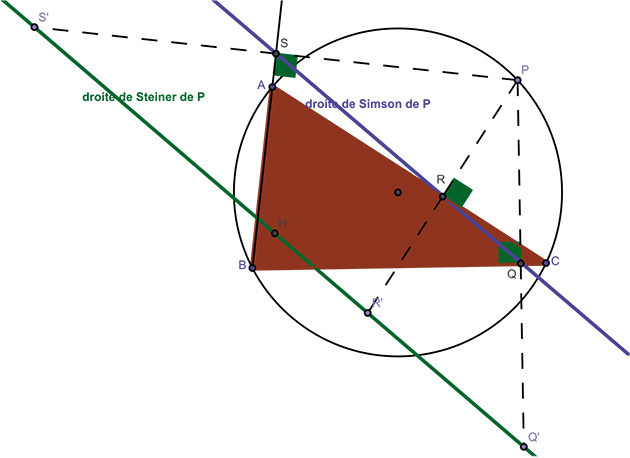
Quels points la droite de Simson contient-elle ? À partir d'un triangle ABC, si on projette orthogonalement un point P quelconque du plan sur les côtés du triangle, ces projections sont alignées si, et seulement si, P appartient au cercle circonscrit au triangle ABC. La droite ainsi associée au point P est sa droite de Simson. La démonstration se fait en utilisant des angles orientés de droites.

Au lieu de considérer les projetés orthogonaux de P sur les côtés du triangle, on peut aussi considérer les symétriques de ce points par rapport aux côtés du triangle ABC. Ils sont également alignés si, et seulement si, P appartient ici encore au cercle circonscrit au triangle ABC ! La droite de cet alignement est alors image de la droite de Simson par l'homothétie de centre P et de rapport 2. C'est la droite de Steiner de P relative au triangle ABC. Elle possède en outre la propriété remarquable de passer par l'orthocentre H du triangle ABC.

La droite d'Euler

« Certaines découvertes d'Euler sont de telle nature qu'on peut très bien imaginer le fantôme d'Euclide dire : “Pourquoi, sur Terre, n'y ai-je pas pensé ?” » affirmait H.S.M. Coxeter. La droite d'Euler est de celles-là. C'est sur cette droite, nommée ainsi en hommage au fameux savant suisse, que s'alignent trois points remarquables du triangle, l'intersection des hauteurs (orthocentre), celle des médianes (centre de gravité) et celle des médiatrices (centre du cercle circonscrit).

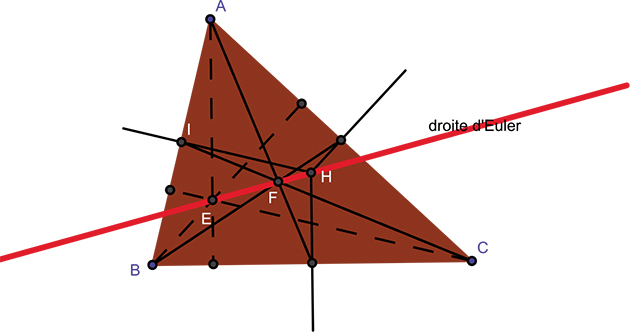
Nommons ces points, comme Euler, respectivement E, F et H. Après de laborieux calculs, c'est par des calculs de distances qu'Euler, en 1767, dans son ouvrage bien nommé Solution facile de certains problèmes très difficiles en géométrie, arrive à prouver que   et  Il en conclut que les trois points sont alignés. Nous dirions aujourd'hui que  et prouverions la propriété en quelques lignes, à l'aide d'un simple calcul vectoriel, qui s'est formalisé à peu près cent ans après sa mort.