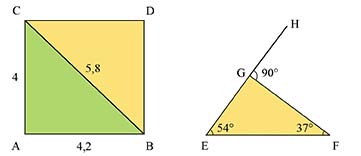
En mathématiques, une conjecture est une assertion que l'on pense vraie mais que l'on ne sait pas prouver. Pris dans ce sens, tout mathématicien, petit ou grand, produit des conjectures quand il fait face à un problème. Par exemple, en plaçant les points comme indiqués sur la figure suivante, on peut être amené à conjecturer que le parallélogramme ABCD est un rectangle et que les trois points E, G et H sont alignés.

 

Ce qui fait une bonne conjecture

De même que, ordinairement, on ne donne pas le nom de théorème à toute assertion vraie des mathématiques, on réserve celui de conjecture à celles qui, non seulement résistent aux mathématiciens pendant un certain temps, mais qui, de plus, sont de nature à faire progresser les mathématiques. Les plus célèbres d'entre elles ont en outre le mérite d'être compréhensibles par un grand nombre de personnes instruites. De ce seul point de vue, la conjecture de Goldbach, qui date de 1742, remodelée par Leonhard Euler (1707-1783, représenté ci-dessus) à qui elle a résisté comme à tous les grands mathématiciens depuis, est sans doute le meilleur exemple :

Tout nombre pair (à partir de 4) peut être écrit comme somme de deux nombres premiers.

Pour être compris, cet énoncé ne demande que de savoir répondre à deux questions : qu'est-ce qu'un nombre pair ? qu'est-ce qu'un nombre premier ? Par ailleurs, ce résultat est facile à vérifier pour de petits nombres :

4 = 2 + 2, 6 = 3 + 3, 8 = 3 + 5,10 = 3 + 7, 12 = 5 + 7… 98 = 19 + 79… 1 000 = 17 + 983…

Mais tous ces exemples ne suffisent pas pour le démontrer !

Cette belle conjecture a suscité des recherches sur la répartition des nombres premiers, un domaine important au niveau théorique et même pratique depuis que la factorisation des nombres a pris de l'importance en cryptologie.

Un dernier ingrédient des bonnes conjectures est le nombre de « preuves » plus ou moins maladroites qu'elles génèrent. Ainsi, la Rédaction de Tangente reçoit toujours des « preuves » de l'hypothèse de Riemann (voir plus loin), comme des « réfutations » de divers résultats mathématiques qui furent longtemps des conjectures (indépendance du cinquième postulat d'Euclide, caractère non dénombrable de l'ensemble des réels…) et des constructions, évidemment fausses, de problèmes prouvés sans solution (dernier théorème de Fermat, quadrature du cercle, trisection de l'angle…). La conjecture de Goldbach arrive championne toutes catégories : elle est très régulièrement « démontrée » par des amateurs ou des semi-amateurs. Certains savent ce qu'est une démonstration et sont sensibles à une réponse pointant leur erreur, d'autres l'ignorent et s'insurgent de la réponse qui leur est transmise, qui est vue comme le mépris d'un tenant de la science officielle à leur égard. Parmi ceux-ci, quelques-uns déposent même leurs « preuves » à la Société des gens de lettres ou à l'Institut national de la protection industrielle (!) et nous le signalent, de peur sans doute de se les faire voler. Parfois, certains médias généralistes et hautement non qualifiés pour ce genre d'expertise s'en mêlent, en défendant ces preuves erronées pour des raisons idéologiques (ce qui est insensé car, en mathématiques, de tels arguments sont sans valeur).

Les grandes conjectures actuelles

Parmi les grandes conjectures actuelles, certaines sont compréhensibles sans bagage mathématique important, au moins dans leurs enjeux. Dans celles-là, on trouve un bon nombre d'assertions sur les nombres premiers, ou les concernant. Mis à part la conjecture de Goldbach, la plus célèbre concerne l'existence d'une infinité de nombres premiers jumeaux qui, comme 5 et 7, sont distants de deux unités. Contrairement à la conjecture précédente, celle-ci n'est attribuée à personne. La seule certitude est qu'elle apparaît en 1849 dans un article d'Alphonse de Polignac, qui la généralise sous la forme suivante :

Tout nombre pair est la différence de deux nombres premiers consécutifs d'une infinité de manières.

Des progrès spectaculaires ont été obtenus très récemment, après des décennies d'incertitude : la conjecture faible de Goldbach (selon laquelle tout nombre impair supérieur à 7 est somme de trois nombres premiers) a été démontrée par Harald Helfgott en 2013. Au même moment, Yitang Zhang prouvait qu'il existe un nombre pair vérifiant la conjecture de Polignac (voir Tangente 153).

De même, l'hypothèse de Riemann est une conjecture sur les nombres premiers, camouflée sous des dehors analytiques puisqu'elle concerne les zéros d'une fonction complexe. En effet, la fonction zêta de Riemann se trouve liée à la répartition des nombres premiers (voir l'encadré). Quiconque arrivera à prouver cette conjecture gagnera un million de dollars : c'est l'un des problèmes de la liste établie par un couple de généreux mécènes, Landon Clay et son épouse Lavinia.

La conjecture de Collatz, ou de Syracuse, venue de Lothar Collatz dans les années 1930 puis étudiée dans les années 1950 à l'université de Syracuse aux États-Unis, est également compréhensible à un niveau relativement élémentaire. Elle porte sur la suite d'entiers définie par la donnée d'un premier terme u₀ et par la formule de récurrence  . Par exemple, si l'on part de 11, on obtient successivement : 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, puis ces trois derniers nombres se répètent indéfiniment dans une boucle. Vous pouvez essayer d'autres valeurs de départ, vous finirez a priori toujours avec ce cycle 4, 2, 1. Mais personne pour l'instant n'a réussi à démontrer ce résultat ! C'est sans doute la raison pour laquelle, là encore, les amateurs sont légions à s'y consacrer. Le grand mathématicien hongrois Paul Erdös (1913-1996), grand résolveur de problèmes (voir Tangente 152), affirmait que les mathématiques ne sont pas prêtes pour de tels problèmes. Depuis, on a mis le doigt sur le verrou mathématique qu'avait pressenti Erdös : les outils issus de la théorie de la transcendance (en théorie analytique des nombres) ne semblent pas assez puissants pour étudier la répartition relative des puissances de 2 et des puissances de 3 dans l'ensemble des entiers. Or, il est nécessaire de prouver qu'il existe des écarts exponentiels entre les puissances de 2 et de 3 pour espérer dompter la conjecture de Collatz. C'est certes un progrès, mais tout reste à faire dans ce domaine !

Indécidabilité ?

D'autres mathématiciens ont exprimé l'opinion que des conjectures résistantes à la preuve (comme celle de Goldbach ou celle de Collatz) pourraient être indécidables, c'est-à-dire improuvables dans la théorie axiomatique utilisée. Par exemple, le postulat d'Euclide ne peut être prouvé en géométrie, sauf à l'admettre comme axiome. De fait, il existe des géométries dans lesquelles ce postulat est faux. Si la conjecture de Collatz, par exemple, était indécidable dans l'axiomatique utilisée en arithmétique, cela signifierait que l'on pourrait l'ajouter aux autres axiomes pour obtenir une nouvelle théorie. Cependant, force est d'avouer que si le postulat d'Euclide est un axiome « naturel », celui-ci ne le serait pas !

L'une des conjectures importantes à l'heure actuelle concerne le temps d'exécution des algorithmes informatiques, que l'on modélise en parlant de complexité (voir les Démonstrations, Bibliothèque Tangente 55). De façon générale, un algorithme fournit un résultat à partir de données dont on mesure la taille par un entier n. L'algorithme est dit de complexité polynomiale s'il existe un nombre entier positif k et un nombre positif A tel que son temps d'exécution soit majoré par An^k. Un problème pour lequel on peut trouver un algorithme en temps polynomial est dit P. Par exemple, le tri est un problème P, le problème du voyageur de commerce (qui doit visiter n villes différentes reliées par un certain nombre de routes en minimisant la distance parcourue) semble ne pas l'être.

Une telle classification suppose l'utilisation des machines usuelles, dites déterministes, où, après chaque action, en vient une autre bien déterminée. Un problème est dit NP s'il existe une machine non déterministe le résolvant en temps polynomial. Décrire une telle machine est abstrait. Il est cependant possible de comprendre pourquoi le problème du voyageur de commerce est NP sans rentrer dans ces détails. Imaginez seulement disposer d'une infinité d'ordinateurs identiques. À chacun, nous faisons calculer la distance d'une route possible. Chaque résultat est obtenu en temps polynomial. Si un super-ordinateur peut alors trouver le plus petit de ces nombres instantanément, le temps total reste polynomial. En première approximation, on peut se représenter notre machine non déterministe comme l'assemblage impossible décrit ci-dessus. Bien entendu, l'intérêt de ces machines imaginaires est que l'on sait montrer qu'un grand nombre de problèmes difficiles sont NP alors qu'on ne sait pas s'ils sont P. La question importante est de savoir si P = NP. On a de bonnes raisons d'en douter car cela signifierait que l'on peut résoudre le problème du voyageur de commerce en temps polynomial. Cependant, le problème reste ouvert et fait partie des sept problèmes que la fondation Clay a dotés d'un prix d'un million de dollars pour celui qui le résoudra.

Enfin, les problèmes NP-complets sont ceux qui ne peuvent être résolus en temps polynomial que si P = NP. Le problème du voyageur de commerce est un problème NP-complet ; il en existe un grand nombre d'autres. Trouver un algorithme polynomial pour un problème NP-complet revient donc à résoudre le problème « P = NP ».