Des sauts dans les suites

Tout commence avec le chiffre 1. Décidons de construire une suite en doublant, à chaque étape, le dernier nombre obtenu : on trouve 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1 024, 2 048, 4 096, 8 192, 16 384, 32 768, 65 536…, à savoir la suite des puissances de 2. Classique !

Introduisons maintenant une « loi d’interruption » dans ce processus : la suite s’arrête dès qu’un terme contient au moins un chiffre en plusieurs exemplaires. C’est le cas ici avec 65 536, qui comporte deux « 5 » (et aussi deux « 6 »). La suite s’interrompt net. Fixons une « loi de reprise » : la suite reprend avec le nombre obtenu en effaçant du dernier terme (ici 65 536) tous les chiffres qui ont des copies. On enchaîne donc avec 3, et la suite devient alors 65 536, 3, 6, 12, 24, 48, 96, 192, 384, 768, 1 536, 3 072, 6 144 (interruption), 61 (reprise), 122 (interruption), 1 (reprise), lequel terme nous ramène au début de la procédure.

Sortir des boucles

Ce genre de boucle est amusant et pose déjà quelques questions arithmétiques (comment caractériser les suites qui vont boucler ? quelle est la longueur moyenne d’une suite qui boucle ?). Mais la façon la plus élémentaire d’échapper aux boucles est d’introduire une autre loi de reprise : après une interruption, décidons de redémarrer la suite avec le plus petit terme absent de la suite. Ainsi, le nombre 65 536 a-t-il pour successeur à 3 (puisque 1 et 2 figurent déjà dans la suite), puis à 6 144, comme précédemment, mais au lieu de poursuivre avec 61, on continuera avec 5, qui est à ce stade le plus petit terme absent de la suite). On obtient 6 144, 5, 10, 20, 40, 80, 160, 320, 640, 1 280, 2 560, 5 120, 10 240 (interruption à cause des deux « 0 »), 7 (plus petit entier qui ne figure pas dans la suite), 14, 28, 56, 112 (interruption), 9 (reprise), 18… On est assuré de ne pas entrer dans une boucle à condition d’accepter que le terme relançant la suite puisse lui-même contenir des chiffres en plusieurs exemplaires. Tous les nombres naturels seront ainsi visités, au moins une fois.

Définies en hommage à l’Américain Stephen Wolfram, les règles de Marflow (palindrome de « Wolfram ») s’appliquent à toute suite définie de manière multiplicative : on décide de l’arrêter quand apparaît (dans le résultat de la dernière multiplication) un chiffre bien précis. Ainsi la suite M₁₇₃ (cf. https://oeis.org/A328086) commence-t-elle par 1, avance-t-elle en multipliant chaque fois son dernier terme par 7, et s’arrête-t-elle dès qu’un 3 surgit (d’où son nom). La loi de reprise consiste là aussi à prolonger la suite avec le plus petit nombre absent de M₁₇₃, même si ce dernier comporte un 3 : M₁₇₃ = 1, 7, 49, 343 (interruption), 2 (plus petit entier pas encore écrit), 14, 98, 686, 4 802, 33 614 (interruption), 3 (reprise et interruption), 4 (reprise), 28, 196, 1 372, 5, 35, 6, 42, 294, 2 058, 14 406, 100 842, 705 894, 4 941 258, 34 588 806, 8, 56, 392, 9, 63, 10, 70, 490, 3 430, 11, 77, 539, 12, 84, 588, 4 116, 28 812, 201 684, 1 411 788, 9 882 516, 69 177 612, 484 243 284, 13, 15…

On définit de manière générale, comme l’a fait Stephen Wolfram pour indexer les deux cent cinquante-six rules (règles) qui gouvernent ses automates cellulaires unidimensionnels, les suites M_abc : le chiffre a en est le premier terme, le chiffre b le multiplicateur et c le « chiffre-stop ».

Jean-Marc Falcoz a calculé les dix mille premiers termes de chacune des huit cent quatre-vingt-dix suites de Marflow issues des chiffres a, b et c. Vous apprécierez tout particulièrement M₁₅₉, qui contient plusieurs blocs de dix-neuf termes consécutifs sans chiffre « 9 ». Amusez-vous par exemple à reconstituer le bloc qui démarre avec 2 176 ou celui qui commence avec 2 048…

Des pyramides et des palindromes

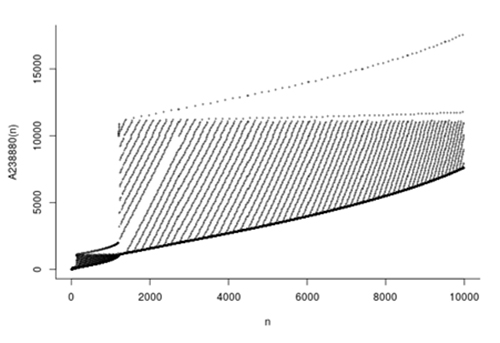
Les lois d’interruption et de reprise engendrent souvent des graphes surprenants. Certains possèdent assurément un caractère fractal. C’est le cas du graphe de la suite que voici (cf. https://oeis.org/A238880), qui évoque une succession de hachoirs de plus en plus grands, lames tournées vers le ciel. Le principe : enchaîner des paires de termes qui, concaténés, dessinent un motif palindrome. Chaque paire commence par le plus petit nombre absent de la suite elle-même : 0–10, 1–11, 2–12, 3–13, 4–14, 5–15, 6–16, 7–17,
8–18, 9–19, 20–102, 21–112, 22–122, 23–32, 24–42, 25–52, 26–62… Entre les paires de termes apparaissent régulièrement des « sauts », qui font le charme de ces suites.

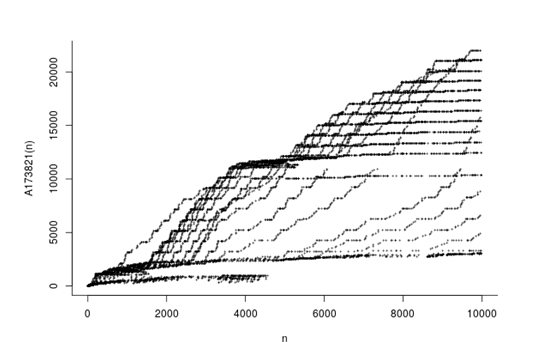
Une autre définition toute simple conduit à une suite spectaculaire, dont le graphe évoque la pyramide du Soleil, à Teotihuacan, au Mexique (cf. https://oeis.org/A173821) : on demande que la somme des chiffres du terme k soit « visible » dans le terme k + 1, lequel doit être le plus petit ayant cette propriété et non encore présent dans la suite. On obtient donc, successivement : 1, 10, 11, 2, 12, 3, 13, 4, 14, 5, 15, 6, 16, 7, 17, 8, 18, 9, 19, 100, 21, 23, 25, 27, 29, 110, 20, 22, 24, 26, 28, 101… Par « visible », il faut comprendre que l’écriture de la somme du k^ème terme figure dans le terme suivant. Ainsi, le nombre 2 019 sera suivi de 1 294 et l’entier 2 020 générera 344.

L’étude de toutes ces suites réserve bien des heures de plaisir arithmétique à l’amateur de récréations avec les nombres !

 [encadre]

En toutes lettres aussi !

La langue française appliquée aux nombres peut être source de phénomènes surprenants. Regardez cette suite (cf. https://oeis.org/A330425) : 1, 13, 20, 2, 30, 3, 40, 4, 50, 5, 9, 10, 7, 17, 6, 15, 8, 26, 100, 11, 16, 18, 60, 12, 109, 35, 209, 65… Ici, un terme A et son voisin B (de gauche ou de droite) ont une somme qui s’écrit avec la même quantité de lettres « consommées » par A et B. Ainsi « un + treize = quatorze » est-il « doublement vrai » car on a la même quantité de lettres (huit lettres) à gauche et à droite du signe « = ».

De même pour « treize + vingt = trente-trois » (onze lettres), « vingt + deux = vingt-deux » (neuf lettres), ou, tout à la fin, « deux cent neuf + soixante-cinq = deux cent soixante-quatorze » (vingt-quatre lettres). Cette suite est lexicographiquement la première à ne proposer que des nombres distincts ; elle existe aussi en anglais (cf. https://oeis.org/A330365). D’autres langues n’attendent que vos talents !

[/encadre]