
Le 2 décembre 2018, Bordeaux reçoit le PSG lors de la quinzième journée de Ligue 1 de football. Ce sera le premier match nul pour le PSG depuis le début de la saison. Score final : 2–2. Vous avez vu le match ? Les amateurs, assidus pendant la rencontre, disent que le PSG aurait dû gagner. C’est d’ailleurs ce que les pronostics d’avant match laissaient croire…
Avant le match…
Pour établir des pronostics, les méthodes sont nombreuses. Du doigt mouillé au machine learning, du parieur du dimanche aux multinationales de paris sportifs, de la lecture de la presse sportive au Big Data, chacun a sa méthode (voir en particulier les dossiers « Mathématiques et sports », Tangente 168, 2016, et « Les mathématiques des paris », Tangente 175, 2017). Entre ces extrêmes, il existe une méthode relativement simple, celle du classement Elo.
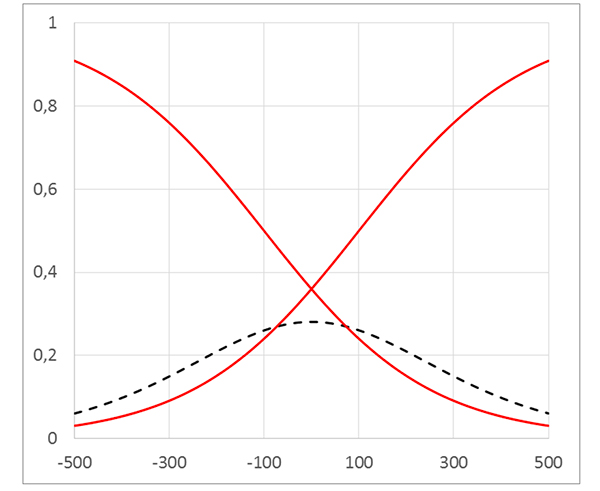
Probabilités de victoire, de défaite et de nul d’une équipe en fonction de l’écart de classement Elo (C = 100).
C’est en 1960 que la Fédération américaine des échecs met en place cette procédure originale proposée par le scientifique et joueur d’échecs Arpad Imre Elo (1903–1992), d’origine hongroise. Le principe permet simultanément de classer les joueurs et de proposer des probabilités de victoire et de défaite en fonction des écarts de classement. Pour classer des joueurs ou des équipes (ici on parle de football), rien de plus simple. À l’initialisation du classement, toutes les équipes ont le même score Elo (par exemple mille points). À chaque rencontre, en fonction de l’issue, un certain nombre de points sont échangés entre les deux équipes : l’équipe qui perd donne une partie de ses points à celle qui gagne. Rapidement, les équipes « fortes » (qui gagnent souvent) ont des scores Elo élevés, et les équipes « faibles » (qui gagnent peu souvent) des scores… faibles.
Lorsqu’une équipe e1 à bas score Elo rencontre une équipe e2 à fort score Elo, l’échange de points dépend de l’issue de la rencontre. Si e1 gagne, alors le nombre de points échangés est grand. Dans le cas inverse, peu de points seront échangés.
Le classement Elo
Lorsqu’une équipe de référence ei rencontre une équipe ej , elles s’échangent un nombre de points égal à K × | Oi, j – Ei, j |, où Ei, j est l’issue espérée de la rencontre pour l’équipe ei et Oi, j le résultat de la rencontre pour cette même équipe ei . Pour un match de football, Oi, j = 0 pour une défaite, Oi, j = 0,5 pour un nul et Oi, j = 1 pour une victoire. La constante positive K définit la volatilité du classement, c’est-à-dire la quantité de points échangés pour un écart | Oi, j – Ei, j | donné.
L’équation la plus caractéristique du classement Elo réside dans le calcul de l’issue espérée (les valeurs Ei, j ). On a :
La constante C est en relation avec la part des matchs nuls (au tennis par exemple, C = 0 ; au football, C = 100 est une valeur assez pertinente). On voit par exemple que si Eloi est « très supérieur » à Eloj , alors Ei, j est « proche » de 1. Ei, j est la probabilité estimée, via Elo, que l’équipe ei remporte la victoire sur l’équipe ej .
Il reste maintenant à définir les probabilités que l’équipe ei perde le match et celle d’un match nul.
Elles valent respectivement :
et
Avant la rencontre, le pronostic peut donc être réalisé sur la base des classements Elo des deux équipes ei et ej . Pour gérer l’avantage (incontestable) de jouer à domicile, les formules des trois probabilités sont modifiées par une augmentation temporaire « artificielle » du classement Elo de l’équipe à domicile.
Mais les pronostics sont faits pour être déjoués ! Le PSG était donné gagnant et le résultat fut 2–2. Bien sûr, on ne peut pas parler d’un « échec des pronostics ». Mais si l’on s’intéresse au déroulement de la rencontre, on pourrait penser que le PSG « aurait dû » gagner. Pour le comprendre, rien de tel que les « buts espérés » (ou expected goals).
Les buts espérés sont une estimation du nombre de buts qu’une équipe « aurait dû » marquer lors d’un match. Ce calcul se fonde sur l’analyse statistique des déroulés des matchs passés. Dans sa version la plus simple, il est basé sur les tirs tentés lors du match étudié. À chaque tir est associée une probabilité de but, basée sur la distance, l’angle de tir et la partie du corps avec laquelle le tir a été effectué. Ces probabilités de buts sont ensuite sommées afin d’obtenir l’expected goal de chaque équipe. De fait, les grandes équipes de football emploient aujourd’hui de nombreux statisticiens, tout comme au basketball aux États-Unis ! Voilà une retombée inattendue de l’élaboration du calcul des probabilités datant du XVII e siècle…

Position des tirs (les surfaces des cercles traduisent les probabilités de buts
et celles des étoiles, les buts), score final et buts espérés.
Au football, où l’occurrence de buts est souvent faible, le score final ne fournit pas toujours une image fidèle de la performance des équipes. En appréciant statistiquement la qualité des opportunités de buts créées et concédées, l’analyse est plus fine, plus objective.
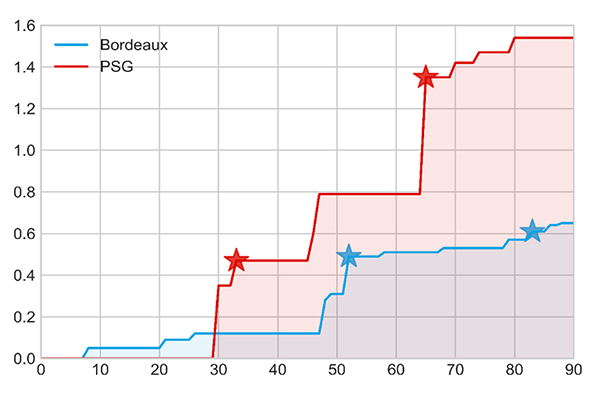
Buts espérés des deux équipes au cours du match.
Bien que le PSG ait moins tenté sa chance lors de la rencontre, les tirs du club de la capitale étaient statistiquement plus dangereux. Ainsi, avec seulement neuf tirs, le PSG obtient un but espéré de 1,54. A contrario, les Girondins de Bordeaux, ayant réalisé dix-huit frappes, ont obtenu un but espéré de 0,65 à la fin de la rencontre. Le PSG aurait-il dû gagner ?
La survenue d’un but ou l’issue d’un match de football fait parfois davantage penser au résultat d’un hasard sauvage qu’à celui d’un hasard bénin. Le classement Elo se fonde actuellement sur les résultats des rencontres (de type pari 1N2 : victoire de la première équipe, match nul, victoire de la seconde équipe). Sans parler de l’intégration des buts espérés dans une intelligence artificielle dont le pouvoir prédictif serait inédit, imaginez déjà des pronostics Elo basés sur ces calculs !
Lire la suite