
En 2007, la très honorable revue américaine Science publiait un article de Peter Lu (voir les références en fin d'article) et de son directeur de thèse, le célèbre physicien Paul Steinhardt.
La première partie de l’article présente une analyse de motifs pentagonaux persans faisant intervenir un pavage intermédiaire caché, fait de cinq types de polygones équilatéraux décorés, les tuiles de nœuds (ou girih tiles). La seconde partie, en s’appuyant sur cette manière de voir, prétend démontrer que les artistes traditionnels avaient découvert les pavages non périodiques (ou quasi-cristaux plans), cinq siècles avant la science occidentale.
Le caractère spectaculaire du propos, allié à la notoriété de Steinhardt, fit que cet article sera repris, et simplifié jusqu’à la caricature, par un grand nombre de journaux à travers le monde (voir Découpages et Pavages, Bibliothèque Tangente 64, 2018).
Pourtant, les deux thèses avancées et présentées comme originales sont pour le moins discutables, et ne rendent pas justice
aux travaux antérieurs, comme ceux de l’Américain Jay Bonner ou du Danois Emil Makovicky.
Faute de place, seule la première thèse sera démontée ici, et quelques arguments seront fournis pour contredire la seconde. Le lecteur curieux est invité à consulter les références pour en savoir plus.
Les motifs pentagonaux de style persan

Figure 1. Un exemple original de motif de la famille « Kond + Sholl ». L’apparente complexité s’évanouit lorsque l’on simplifie le motif, en éliminant les variations. Essayez donc de reconnaître toutes les étoiles à dix pointes (solution Figure 6).
La méthode d’analyse présentée par Lu et Steinhardt comme leur découverte avait été proposée en 1925 par E. H. Hankin, puis améliorée par J. Bonner et C. Kaplan. L’idée est séduisante : pour comprendre le visible, il s’agirait d’être initié à l’invisible. Le point de vue alternatif présenté ici, qui n’utilise que les pièces visibles, est très proche de la tradition des artisans persans, puisqu’il conduit à définir les mêmes familles de motifs. Il existe deux familles de motifs pentagonaux traditionnels : la première est nommées « Tond » en persan ; la seconde, « Kond + Sholl », utilise un jeu de pièces principal et un jeu complémentaire. Les cinq « tuiles de nœuds » de Peter Lu ne peuvent engendrer que des motifs de la sous-famille « Kond », la plus représentée. De plus, les prétendues preuves historiques de l’utilisation de cette méthode sont discutables...
La relation existant entre le pavage visible et le pavage polygonal « caché » n’est autre qu’une simple dualité : on peut passer de l’un à l’autre et réciproquement, ce qui affaiblit considérablement l’argument de primauté du pavage polygonal.
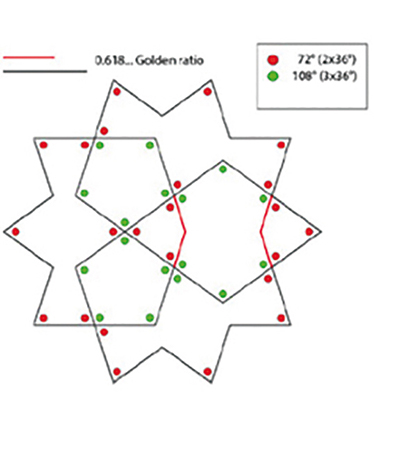
Figure 2. La « mère » de toutes les pièces de la famille « Kond ». Seulement deux longueurs interviennent, qui sont naturellement dans le rapport du nombre d’or,
et deux angles, multiples de 36°. En toute simplicité !
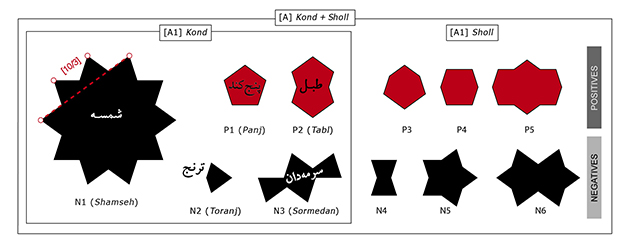
Figure 3. Ensemble [A] des pièces de la famille pentagonale « Kond + Sholl »
(les pièces positives sont en rouge, les négatives en noir).
Encadré à gauche, le sous-ensemble « Kond » [A1].
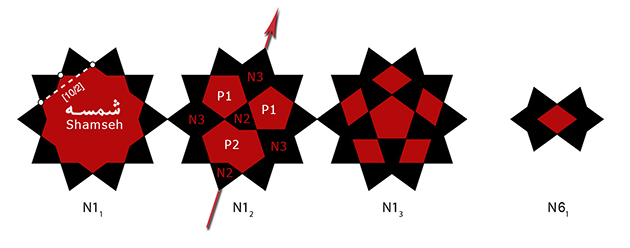
Figure 4. La « mère » (décagone étoilé noté N1 ou [10/3]) n’est jamais représentée nue, mais toujours dans l’une de ses variations.
Seule la variation N11 (avec un décagone [10/2]) conserve les symétries,
N12 est orientée et N13 utilise une nouvelle pièce.
À droite : l’unique variation, N61, de la pièce N6.
Tout motif de ces familles peut être coloré comme un damier, en deux couleurs (puisque les lignes ne se croisent jamais que par deux). Chose remarquable : dans ce cas, tout exemplaire d’une même forme sera toujours de la même couleur. Ces ensembles sont donc divisibles en deux catégories de pièces, que l’on nommera – arbitrairement – positives et négatives. En conséquence, tout motif de ces familles pourra être construit en n’utilisant que des pièces positives (respectivement négatives), correctement agencées, séparées par des vides qui prennent nécessairement la forme de pièces négatives (respectivement positives). Les règles d’assemblage sont évidentes : pièces jointives par sommet, continuité des lignes au niveau des points de contact. Ainsi donc, tout motif de la famille « Kond » peut être construit en n’utilisant que les deux pièces positives (ou trois avec le décagone [10/2] de la variation N11). Encore mieux que les cinq « tuiles de nœuds » ! Enfin, dans cette famille, l’étoile polygonale, « mère » de toutes les autres, est rarement représentée nue, mais toujours décorée par d’autres pièces. C’est pourquoi la première tâche à entreprendre pour comprendre un motif de la famille « Kond + Scholl » consiste à le simplifier : repérer les étoiles et les « déshabiller » (Figures 1 et 6).

Figure 5. Ce motif est le plus simple de la seconde famille de motifs pentagonaux persans, « Tond ». On le rencontre partout en terre d’islam, de Grenade à l’Inde du nord. Cet article traite de la première famille, nommée « Kond + Sholl » en persan.

Figure 6. La véritable genèse du motif de la Figure 1, construit directement avec les pièces. L’idée est de partir d’une couronne de dix étoiles, avec une étoile au centre. Quoi de plus simple et naturel ? Nul besoin de « tuiles de nœuds » ! On résout ensuite les problèmes de raccord, extérieur et intérieur (aucune difficulté... avec un peu d’entraînement). Deux solutions différentes de raccord intérieur ont été utilisées ici (au centre et à droite), et des variations ont été introduites (en rouge) sur les étoiles et sur les pièces N6.
L’analyse présentée par Lu et Steinhardt comme un système historique de conception et réalisation consiste à construire un pavage de polygones équilatéraux, les fameuses tuiles de nœuds, puis à tracer, à partir du milieu de chaque côté, deux lignes symétriques qui vont se rencontrer à l’intérieur des polygones. En éliminant les côtés du pavage polygonal, on verra apparaître un motif traditionnel. Mais cette construction ne fait que déplacer le problème : comment construire ce pavage polygonal ?
Dessinons sur chaque pièce positive de la famille « Kond + Scholl » les lignes représentées sur la figure 7. Assemblons les pièces « au hasard », tout en respectant les règles d’assemblage. Certaines de ces lignes rencontrent une amie, d’autres non. Éliminons donc les orphelines. Que reste-t-il ? Un pavage polygonal isométrique ! S’il est vrai qu’un tel pavage engendre un motif traditionnel, la transformation fonctionne donc aussi bien dans l’autre sens. La relation entre les deux structures n’est qu’une forme de dualité !
La méthode polygonale n’est pourtant pas dénuée d’intérêt. Il est simplement question ici d’interroger la prétention historique, puisque le caractère dual de la relation affaiblit considérablement la thèse de Lu et Steinhardt.
L’épineuse question de la présence des « quasis »
La deuxième partie de l’article de 2007 en constitue la thèse la plus ambitieuse. Les auteurs considèrent un fameux motif à deux niveaux (il y a « du motif dans le motif », comme disent les artisans iraniens), selon le point de vue des « tuiles de nœuds ». Ils arrivent ensuite à le découper selon un pavage de Penrose (dans la version « flèches et cerf-volants »), en corrigeant au passage des « erreurs » qu’auraient faites les artisans, et finissent par conclure qu’il s’agit d’un motif non-périodique (ou quasi-cristal plan). Les artistes persans auraient donc découvert ces notions cinq siècles avant la science occidentale.
La place manque ici pour discuter en profondeur cette thèse. Quelques remarques cependant.
Tous les motifs analysés par les auteurs sont des motifs périodiques, parfois tronqués par la courbure d’un arc. Par contre, le procédé d’inflation mis en œuvre dans les motifs à deux niveaux pourrait engendrer des pavages parfaitement auto-similaires, à symétrie locale pentagonale, donc à une forme de quasi-cristal, si l’on arrivait à le rendre complet. Il y a donc, dans la tradition, une potentialité de « quasis ».
Les motifs pentagonaux persans à deux niveaux sont incomplets dans le sens ou les règles d’inflation qui, en remplaçant chaque type de pavé par un ensemble de pavés à une échelle réduite, permettent de passer d’un niveau au suivant, sont définies pour toutes les pièces... sauf pour une, le « Sormedan » (N3 dans la figure 3). Cette pièce ne figure jamais au premier niveau du motif (sauf exception, mais sans inflation convenable), mais toujours au second. Plusieurs solutions sont proposées dans notre article cité en référence.
La figure ci-contre montre une solution de mise en abyme du Sormedan faisant intervenir toutes les pièces de la famille « Kond + Sholl ».
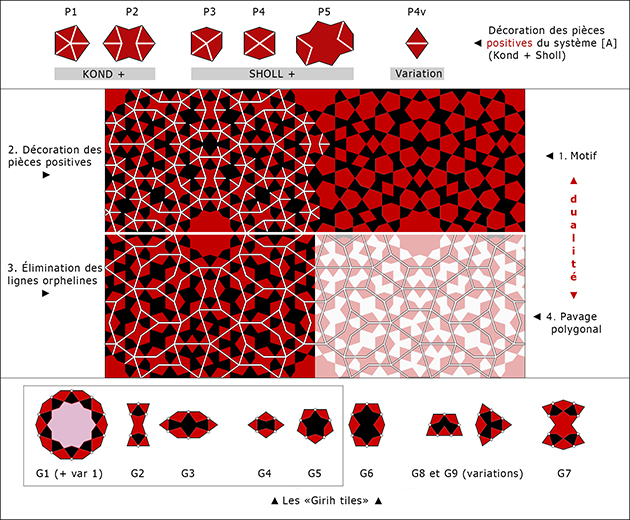
Figure 7. La décoration des pièces positives (en haut) permet de mettre en évidence la relation de dualité entre le motif et le pavage polygonal associé. Les formes intérieures aux polygones sont les pièces négatives, les positives se forment par l’assemblage de polygones autour des sommets. En bas, les « tuiles de nœuds » associées à la famille « Kond + Sholl ». Encadrées à droite, celles qui sont engendrées par la sous-famille « Kond ». Les polygones G8 et G9, associés aux variations N13 et N61, ne sont pas équilatéraux.
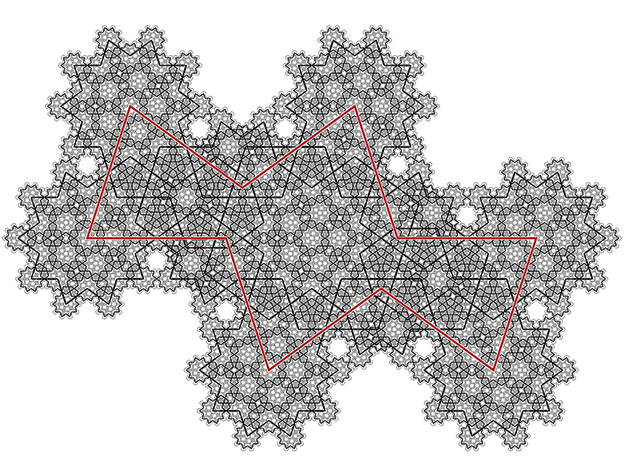
Figure 8. Au premier niveau de cette figure, les lignes rouges dessinent le contour d’une unique pièce, le « Sormedan ». En le décomposant en pièces de la même famille mais à échelle réduite, on obtient un pavage de deuxième niveau, dont chaque pièce subira un traitement similaire, et ainsi de suite. Dans cet exemple il a fallu aller jusqu’au quatrième niveau pour définir un pavage parfaitement auto-similaire (dont toutes les pièces possèdent leur règle de substitution).
Sans utiliser les « tuiles de nœuds » !
Lire la suite