
On sait peu de choses sur la vie d’Adélard. Il a vu le jour près de Wells, vers 1080, soit une quinzaine d’années après la conquête de l’Angleterre par Guillaume le Conquérant. Il vit à Bath, dans le sud-ouest de l’Angleterre, mais, pour parfaire sa formation, il se rend à Tours puis enseigne à Laon. Il effectue de nombreux voyages, d’abord en Sicile, où il entre en contact avec la culture grecque puis, suivant les traces des Croisades, il séjourne à Tarse en Cilicie et à Antioche. Il revient en Occident en 1126 et s’éteint en 1152.
Adélard rédige deux ouvrages fondamentaux. Dans De eodem et diverso (« L’un et le divers »), rédigé vers 1110, il réfléchit à la nature des choses, parmi lesquelles des problèmes de la vie courante résolus par la géométrie. Dans Questiones naturales, écrit sous forme d’un dialogue, il enseigne à son neveu les raisons de nombreux phénomènes physiques mais aussi moraux.
Lors de ses séjours en Orient, Adélard s’initie à la langue arabe. Il traduit alors en latin les tables astronomiques d’al-Khwarizmi ainsi qu’une version des Éléments d’Euclide écrite en arabe. On lui doit de nombreuses autres traductions, depuis l’arabe, de textes scientifiques, ce qui permit à l’Occident d’accéder à de nouvelles connaissances. Il a surtout transmis le conseil de ses « maîtres » arabes, à savoir être guidé par la raison et non par les arguments d’autorité. Cette attitude nouvelle dans l’Occident médiéval mettra trois siècles à s’épanouir pour conduire, à la Renaissance, à l’éclosion de l’esprit scientifique.
Un traducteur d’Euclide en latin
Le mathématicien al-Hajjaj ibn Yusuf ibn Matar travaillait à Bagdad ; il est l’auteur de la première traduction en arabe des Éléments d’Euclide, dédiée au calife Haroun ar-Rachid, qui régna de 786 à 809. Il la réalisa d’après une version grecque venue de Constantinople. Insatisfait de son texte, il en effectua une seconde en l’honneur du calife al-Mamun, qui avait succédé à son père. Un demi-siècle plus tard, une nouvelle traduction des Éléments fut l’œuvre d’Ishaq ibn Hunayn, suivie de peu par celle du célèbre mathématicien Thabit ibn Qurra.
C’est à partir de ces textes arabes qu’Adélard de Bath, de retour du Proche-Orient, effectua une traduction des Éléments. Il était motivé par le souci de diffuser la géométrie d’Euclide auprès de ses étudiants. Son texte, le premier qui nous soit parvenu en langue latine, eut un impact bien supérieur puisqu’il provoqua un intérêt nouveau pour la géométrie dans tout le monde universitaire occidental.

Références :
• L’un et le divers, Questions sur la nature, avec en complément Comme l’atteste Ergaphalau. Adelardus Bathoniensis, Les Belles Lettres, 2016.
• Dossier « Des maths au service de l’histoire ». Tangente 145, 2012.
Calculer la profondeur d’un puits
« La géométrie […] a enseigné le moyen d’évaluer la profondeur de n’importe quel puits. Le mesureur doit commencer par rechercher très précisément si le périmètre du puits est circulaire. Puis mesurer son diamètre. Enfin, debout sur le bord du puits, qu’il pose à ses pieds une planche de bois de n’importe quelle taille : qu’il la déplace par petits coups d’avant en arrière jusqu’à ce qu’il voie le fond de l’autre côté du puits dans l’alignement de l’extrémité de la planche. Puis qu’il établisse le rapport entre la partie qui dépasse du bord du puits et sa taille, et il trouvera le même rapport entre le diamètre et la profondeur du puits augmenté de sa taille.
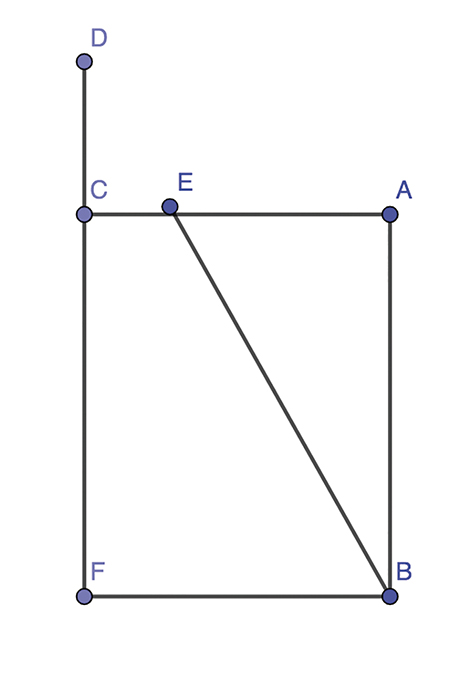
Par exemple, soit CF la profondeur du puits, CA son diamètre, CD la taille du mesureur, CE la partie de la planche, AB l’autre partie du puits. Si DC est le triple de CE, DF sera le triple de CA. » (Extrait de Adelardus Bathonensis, traduction d’Émilia Ndiaye, Max Lejbowicz et Christiane Dussourt)
Le résultat s’obtient par une simple application du théorème de Thalès appliqué aux triangles DFB et DCE, mais Adélard affirme la conclusion sans démonstration.
Lire la suite