Un arbre binaire complet est une structure combinatoire qui se construit à partir d’un point initial (la racine), duquel partent deux segments (des branches, ou arêtes) qui atteignent deux nouveaux points (des nœuds), desquels partent deux nouveaux segments, et ainsi de suite. Les nœuds successifs sont répartis en lignes, les nœuds de la ligne n étant ceux qui sont rejoints en n segments en partant de la racine. Les nœuds de la dernière ligne, desquels ne partent plus de branches, sont les feuilles de l’arbre.

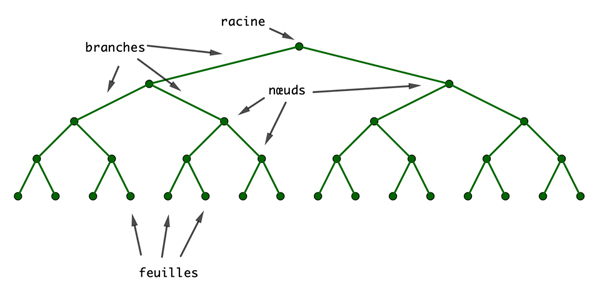
Les notions ainsi définies ressemblent fort à celles qui leur correspondent chez les vrais arbres (ceux en bois), la principale différence formelle étant qu’en combinatoire les arbres ont le plus souvent la racine en haut et les feuilles en bas…

Étiquetons à présent chaque branche selon la marche à suivre pour l’atteindre en partant de la racine, en marquant 0 lorsque l’on va à gauche et 1 lorsque l’on va à droite. On peut interpréter cette étiquette comme l’écriture binaire d’un nombre (voir encadré). En outre, sur le nœud inférieur de chaque arête, écrivons en base 10 la valeur du nombre correspondant. Le nombre 13, par exemple, est l’écriture décimale de « 1101 », qui est l’étiquette de l’arête ainsi atteinte : partant de la racine, on va d’abord à droite (1), puis encore à droite (1), puis à gauche (0) et enfin à droite (1).

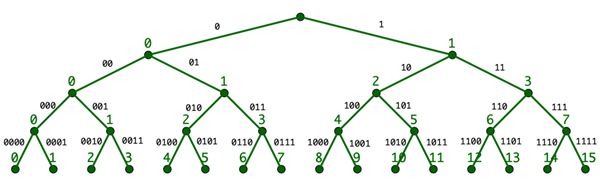
Ne faisons pas d’impair

Comme on le voit, sur chaque ligne on obtient la liste des premiers entiers naturels. Plus précisément, sur la ligne n figurent, dans l’ordre croissant, les entiers de 0 à 2 ⁿ – 1. Cela se démontre à l’aide d’un raisonnement par récurrence (voir FOCUS « La numération binaire »).

Nous avons donc là une manière « naturelle » d’obtenir les entiers écrits en binaire à partir des arbres binaires complets. En ajoutant encore et encore des lignes à l’arbre, on atteint progressivement l’ensemble des entiers, qui apparaît comme l’ensemble des feuilles « à l’horizon ». Le caractère « naturel » de cette construction repose toutefois sur un choix arbitraire : à chaque fois que l’on ajoute une ligne à l’arbre, l’étiquette de chaque nouvelle branche est obtenue en ajoutant un 0 ou un 1 à droite de l’étiquette de la branche dont elle est issue. 

Par exemple, la branche étiquetée 110 donne naissance aux branches 1100 et 1101. D’où la question qui vient facilement aux lèvres : pourquoi ne pas plutôt ajouter chaque nouveau chiffre à gauche ? Ce changement de règle, qui n’a l’air de rien, raconte une histoire complètement différente.

Comme on le voit sur la ligne 4 de l’arbre suivant, les entiers entre 0 et 15 sont toujours tous bel et bien là, mais cette fois dans un ordre qui n’a plus rien à voir avec celui auquel on est habitué. Il s’agit d’un ordre dyadique, dans lequel deux entiers sont « d’autant plus proches » que « beaucoup » de leurs premiers chiffres binaires sont communs.

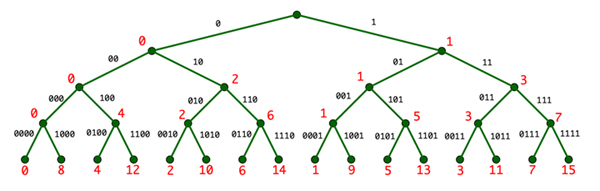
Cet arbre montre les entiers non pas à travers le prisme de leur valeur, mais selon leur degré de parité : les nombres « les plus pairs » sont les plus à gauche, et les « plus impairs » sont à droite. On constate par exemple que les nombres pairs sont sur la moitié gauche de l’arbre, que les multiples de 4 sont sur le quart gauche, et ainsi de suite. Les nombres 1 et 9 de la dernière ligne correspondent, eux, aux nombres « les plus pairs parmi les nombres impairs », ce qui signifie ceci : quand on leur retranche une unité, on obtient un nombre trois fois divisible par 2.

Dans le cas classique, la continuation de l’arbre à l’infini produit l’ensemble des entiers positifs rangés dans l’ordre croissant. Sur notre nouvel arbre, ajouter des lignes indéfiniment produit l’ensemble des entiers dyadiques, ceux où les 0 et les 1 de leur développement binaire « partent à gauche à l’infini ».

Promenons-nous dans les arbres

Bien que voisins, les deux arbres ont des propriétés très différentes. Ainsi, sur l’arbre classique, il est toujours très facile de savoir quels sont les nœuds au-dessus et au-dessous d’une valeur k donnée (les nœuds qui la suivent ont pour valeur 2k et 2k+1, celui dont elle est issue a pour valeur la partie entière de k /2), alors qu’il y a plusieurs possibilités pour une valeur figurant sur l’arbre dyadique. Par exemple, sur la figure précédente, la valeur k = 3 est suivie des valeurs 3 et 7, ou bien des valeurs 3 et 11, selon le nœud où est lue k. De même, il est facile, la valeur k d’un nœud étant donnée sur le premier arbre, de déterminer la position du nœud de valeur k +1 sur la même ligne (il suffit de se décaler d’un cran vers la droite), alors que l’opération n’a rien d’aussi évident sur l’arbre dyadique.

Inversement, la position « limite » d’un entier sur l’horizon dyadique est un peu plus naturelle à localiser : dès lors que cet entier apparaît sur une ligne, on le suit à la trace en descendant indéfiniment vers la gauche.