L'archéologie utilise de nombreuses procédures numériques qui s’appuient sur des mathématiques : photogrammétrie, recherche de régularités numériques (ou, au contraire, preuve qu’elles sont illusoires). Mais, dans un autre domaine, les mathématiques servent à construire des modèles logiques pour tester des raisonnements. Cela a été particulièrement le cas pour l’archéologie et la paléontologie du peuplement, où le modèle de la « vague d’avancée » a acquis un grand renom.

Invasions et sédentaires

Pendant longtemps le peuplement du monde a été décrit comme une suite d’invasions. Les différentes cultures que distinguent les paléontologues étaient expliquées par des invasions et des remplacements de populations. En Eurasie, c’étaient celles venues des steppes de l’Est, puis à la fin de l’empire romain, celles des Germains et des peuples du Nord, puis les Huns d’Attila et les Mongols de Gengis Khan et de Tamerlan. De même, les Européens ont envahi l’Amérique à partir du XV^e siècle. Encore aujourd’hui, certains craignent un « grand remplacement ». Ces mouvements brutaux de population étaient expliqués par la supériorité militaire des envahisseurs, par exemple par l’invention de l’étrier par les Mongols ou par celle des armes à feu pour les conquistadors.

La « théorie des invasions » se heurtait cependant à plusieurs obstacles. Les populations les plus anciennes étaient sédentaires. Les chasseurs cueilleurs du Paléolithique se déplaçaient d’un terrain de chasse et de cueillette à l’autre tout au long de l’année, mais selon un parcours immuable d’une année sur l’autre. Quant aux premiers agriculteurs, ils restaient fixés à leurs champs. Plus on remontait loin dans le passé, moins l’hypothèse d’invasions devenait vraisemblable.

La vague d’avancée

Le Britannique Colin Renfrew, fondateur de la « new archeology », a alors avancé un modèle de peuplement de l’Europe et de l’Asie mineure. Tout se joue dans la progression de l’agriculture. Les effectifs des populations de chasseurs cueilleurs étaient stables en moyenne en raison d’une fécondité assez faible due à de longs intervalles entre naissances : pour être sevrés, les enfants devaient être capables d’ingurgiter des racines et des restes d’animaux, donc d’avoir une dentition assez développée.

Avec l’agriculture, il devient au contraire possible de sevrer les enfants plus jeunes car on peut les nourrir de bouillies de céréales ou de lait. Le raccourcissement des intervalles entre naissances a alors entraîné une augmentation de la fécondité, elle-même cause d’explosion démographique.

De leur foyer initial au Proche-Orient, les populations d’agriculteurs se sont donc progressivement étendues dans toutes les directions. Il leur était facile d’occuper un territoire des chasseurs cueilleurs en raison des différences énormes de densité. On estime qu’un chasseur cueilleur a besoin de dix kilomètres carrés pour assurer sa subsistance, soit une densité de 0,1 habitant. Au contraire, les agriculteurs, avec des pratiques primitives (brûlis et ensuite jachère de vingt années, rendement de cinq quintaux à l’hectare pendant l’année du brûlis) peuvent survivre à cinq personnes par kilomètre carré, soit cinquante fois plus que les chasseurs cueilleurs.

Renfrew a fait appel au mathématicien Albert Ammerman pour modéliser cette idée de progression. Les deux auteurs ont supposé que la population des agriculteurs s’accroissait de 0,5 % par an à partir du lieu d’origine et que lorsque la densité maximale de cinq habitants par kilomètre carré était atteinte, le surplus de population se dirigeait vers les plus proches terres disponibles. Le modèle assez simple montre une extension régulière de la surface cultivée au rythme d’environ trente kilomètres par génération.

Vérification du modèle

Quatre faits sont expliqués par la vague d’avancée. D’abord, et surtout, les datations de l’apparition de l’agriculture en Europe montrent avec une assez grande exactitude la progression régulière à partir de l’Asie mineure dans la direction nord-ouest entre – 9000 et – 4000, date à laquelle l’Irlande est atteinte. Dans le détail, de petits désaccords apparaissent du fait des obstacles géographiques. Ainsi, la progression a été plus rapide par la vallée du Danube que par les montagnes des Balkans.

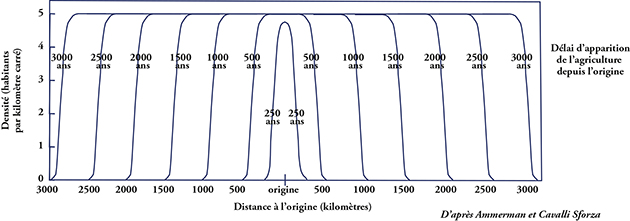
Date de première apparition de l’agriculture en Eurasie.

Deuxième argument, les cartes génétiques de l’Europe établies par le spécialiste de la génétique des populations Luigi Luca Cavalli-Sforza (1922–2018) montrent une direction principale de variation orientée du Sud-est au Nord-ouest, selon la même direction que la progression de l’agriculture. Au cours de leur avancée, les agriculteurs se sont métissés avec les chasseurs cueilleurs et ont aussi connu une dérive génétique.

Troisième argument, d’autres cas de vague d’avancée ont été mis en évidence plus récemment, au sud du Mexique avec la culture du maïs, en Chine méridionale avec celle du riz et en Nouvelle Guinée avec le taro.

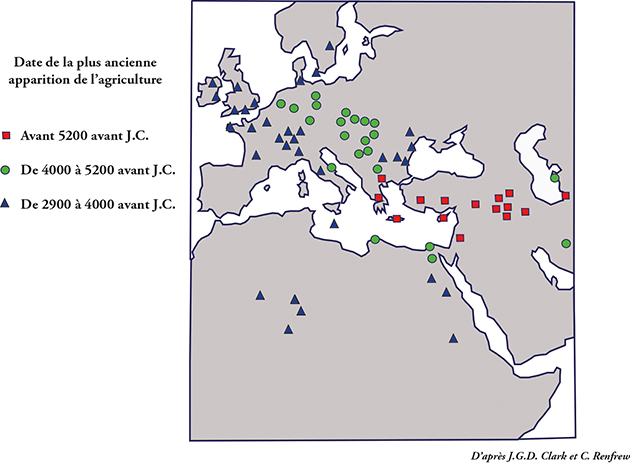
Modèle simple de la progression de l’agriculture en « vague d’avancée »
à partir de sa première apparition (origine).

Enfin, dernier argument, objet de chaudes controverses, les langues indoeuropéennes auraient suivi la progression des agriculteurs et se seraient différenciées progressivement à partir du foyer initial proche oriental.

La première difficulté que soulève le modèle d’Ammerman vient de la dimension : il est à une dimension, tandis que le territoire en possède deux. Dans ce cas, la croissance de la population des zones où la densité maximale est atteinte est proportionnelle au carré de leur rayon en les supposant circulaires. Dès lors, l’avancée annuelle se produit sur une couronne circulaire de largeur proportionnelle au rayon, donc de plus en plus rapide, ce qui ne correspond pas aux observations.

Le cas du Danube permet de contourner la difficulté : si la zone cultivée est constituée par les côtes et les vallées fluviales, on retrouve un modèle linéaire.

On a prouvé récemment que la domestication des animaux avait eu lieu à peu près en même temps que l’expansion de l’agriculture. Plus les terres sont de mauvaise qualité, plus l’élevage prend de l’importance par rapport à la culture céréalière. Il vient un moment où, sur les confins désertiques ou dans les montagnes élevées, l’élevage subsiste seul. Alors les éleveurs deviennent des nomades, à la manière des chasseurs cueilleurs, avec des parcours annuels fixes.

La différence majeure entre agriculteurs et éleveurs est leur mobilité. Les premiers se regroupent difficilement, attachés qu’ils sont à leur terre, les seconds facilement car leurs troupeaux les suivent. Les éleveurs ont ainsi un avantage militaire sur les agriculteurs, sur lesquels ils peuvent fondre en masse. Ils vont en profiter tout au long de l’histoire, jusqu’à aujourd’hui, en Irak, au Yemen, dans le Dar Four ou au Sahel.

Cette question a aussi une grande importance pour l’histoire européenne. Vers le cinquième millénaire avant notre ère, des populations nomades d’éleveurs, les Yanma, venues du nord de la Caspienne et de l’Oural, se sont implantées durablement à l’Ouest. La seconde direction de différenciation génétique trouvée par Cavalli-Sforza est en effet dans le sens Est-Ouest. Elle est confirmée par l’archéologie, sans qu’une précision comparable à celle de l’avancée de l’agriculture puisse être obtenue. Elle a aussi donné une version alternative de l’origine des langues indoeuropéennes, qui se seraient diversifiées au cours de cette migration de nomades.

Enrichir le modèle mathématique

Tous ces éléments obligent à compliquer le modèle de la vague d’avancée. Il faut introduire une différenciation de la productivité des terres et, en fonction d’elle, un partage entre élevage et agriculture. Pour certaines combinaisons de ces deux paramètres, il est alors possible de sauver l’expansion de l’agriculture à vitesse constante, telle qu’observée. Pour cela, on ne doit plus utiliser des modèles analytiques comme celui d’Ammerman mais des simulations numériques où le comportement de chaque agriculteur est défini en fonction de sa position sur le territoire.

Une dernière difficulté logique insoluble subsiste cependant, celle d’une constance de la productivité des terres et du partage entre agriculture et culture en fonction de cette productivité. Or, comme l’a montré l’économiste danoise Ester Boserup (1910–1999), la densité croissante pousse à une transformation des modes culturaux. La jachère longue devient courte, puis annuelle (assolement biennal), ou même une année sur trois (assolement triennal). Les terres sont défrichées, dépierrées, amendées, tout ceci au prix d’un accroissement du temps de travail. En tenir compte dépasse les possibilités de la modélisation précédente mais reste ouvert à de nouveaux modèles.

Tout cela peut donner l’impression d’un échec des modèles à rendre compte de la réalité. Dans ce cas, paradoxalement, ce n’était pas le but. Il ne s’agissait pas de reproduire la réalité comme un portrait reproduit l’apparence d’une personne. Il s’agissait d’aider à questionner cette réalité en en extrayant les éléments les plus évidents pour se concentrer sur les résidus, puis les résidus des résidus. La relation initiale entre croissance de la population au Néolithique et progression régulière de l’agriculture, une fois modélisée assez succinctement par la vague d’avancée, permet à la connaissance de progresser. Ses incohérences logiques, qu’un simple énoncé verbal ne décelait pas, sont mises en évidence et font à leur tour l’objet d’un traitement mathématique par simulation, comme vu précédemment. Puis les incohérences de ces incohérences logiques deviennent elles-mêmes perceptibles et demandent une réponse. Le processus est sans fin car le comportement de chaque agriculteur depuis –10000 ne peut pas être entièrement modélisé, mais seulement approché assez grossièrement, « le moins grossièrement possible », grâce à de tels modèles.