La datation constitue une étape importante lors de l’étude d’un site archéologique. Elle permet de localiser dans le temps la période d’activité du lieu. Combinée avec la statistique, elle fournit  des outils pour répondre à de nombreuses questions : quelle est la période d’activité d’un site ? Quelle est la durée d’occupation ? Le site a-t-il été occupé à plusieurs périodes ? Quelle est la chronologie des périodes d’occupation ?

Différentes méthodes de datation sont disponibles, le choix dépend essentiellement du type de matériel trouvé sur place et de l’âge du site. Toutes ces techniques vont fournir des dates avec une précision qui dépend de la méthode.

Sur un site archéologique, plusieurs objets peuvent être datés. De nombreuses informations complémentaires peuvent être collectées. Par exemple, des considérations stratigraphiques vont imposer une contrainte d’ordre sur les âges. La statistique bayésienne fournit une méthode d’estimation de la période qui prend en compte ces informations, lesquelles sont combinées avec les mesures de datation effectuées en laboratoire sur les objets prélevés.

 
Quelques méthodes de datation

 

La dendrochronologie s’applique sur le bois. Elle repose sur l’épaisseur des cernes, qui est comparée à un référentiel. Sa période d’application se situe entre aujourd’hui et –9000.

Le carbone 14 ( ¹⁴C ) s’applique sur de la matière organique, par exemple des charbons de bois, des ossements, des restes de végétaux. Cette méthode utilise les isotopes du carbone. Le ¹⁴C étant radioactif, il se décompose en ¹²C en fonction du temps. Sa période de décomposition est d’environ cinq mille sept cent trente ans. Connaissant la fonction décroissance du ¹⁴C, il est donc possible de connaître le temps écoulé depuis la mort à partir de la dose de ¹⁴C mesurée en laboratoire.

La thermoluminescence permet de dater des objets contenant des quartz qui ont été chauffés, comme par exemple des céramiques, des matériaux de construction… Des expériences en laboratoire permettent de déterminer l’âge de la dernière chauffe supérieure à environ 400°C. À cette température, les pièges à électrons sont vidés et les électrons émettent de la lumière pour revenir à leur niveau d’énergie.

L’approche bayésienne est une méthode d’estimation qualifiée de probabiliste car l’information sur les dates à déterminer est exprimée sous la forme d’une loi de probabilité. On commence par construire une loi a priori qui résume la connaissance sur les dates sans connaître les résultats du laboratoire de datation. Cette loi a priori va prendre en compte des données historiques, géologiques, archéologiques. On collecte ensuite les mesures effectuées par les laboratoires et la précision de la mesure pour les différents échantillons. Les mesures sont liées à l’âge inconnu par une loi de probabilité.

Le théorème de Bayes (voir FOCUS) permet de combiner la loi a priori et la loi des mesures pour obtenir une nouvelle loi sur l’âge. C’est la loi a posteriori. Elle résume toute l’information disponible sur l’âge. On peut l’interpréter comme une « mise à jour » de la loi a priori à partir des mesures du laboratoire. Les applications de cette méthode sont nombreuses !

 

La calibration d’un âge ¹⁴C

La datation par carbone 14 nécessite une étape de calibration. C’est une correction de l’âge à l’aide d’une fonction g (dite de calibration) étalonnée sur des échantillons dont les dates sont connues via une autre méthode de datation. La statistique bayésienne fournit un outil pour faire cette correction en intégrant une connaissance a priori sur l’âge.

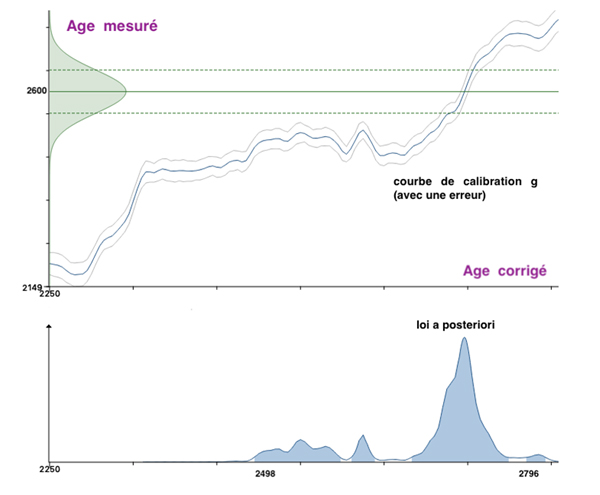
Le laboratoire fournit une mesure M de l’âge cherché (M = 2600 ans) avec une erreur s (ici s = 50 ans). On modélise l’incertitude sur cette mesure par une loi gaussienne (verticalement, la courbe en vert, centrée sur M = 2600). On note θ l’âge inconnu de l’échantillon. La mesure M est liée à θ par sa loi, la gaussienne de moyenne g (θ) et de variance s ².

On va supposer que l’information a priori sur l’âge est « l’âge de l’objet est inférieur à 3000 ans ». On traduit cette information en choisissant comme loi a priori sur l’âge la loi uniforme sur l’intervalle [0, 3 000]. La loi a posteriori est calculée par la formule de Bayes et représentée en bleu. À partir de la loi a posteriori, on peut déterminer un intervalle de crédibilité égal à [2 498, 2 796]. Il contient l’âge avec une probabilité de 95 %. Son amplitude est de trois cents ans. Pour réduire cette amplitude, et ainsi améliorer la précision de l’estimation, il faudrait disposer d’informations supplémentaires pour réduire l’intervalle de la loi a priori uniforme. Ainsi, toute nouvelle connaissance peut permettre d’améliorer la précision de l’estimation.

 
La datation d’un évènement

Une date d’évènement archéologique n’est pas toujours mesurable par une méthode de datation. Par exemple, on ne peut pas dater directement la fin de l’activité d’un atelier médiéval de poterie. Dans une telle situation, on cherche à dater des objets qui sont contemporains de l’évènement à dater. Pour le cas de l’atelier de poterie, on peut dater par carbone 14 des charbons de bois trouvés dans le four, ou par thermoluminescence des morceaux de brique provenant de la structure du four. Le carbone 14 va dater l’abattage de l’arbre, et la thermoluminescence la dernière exposition de la brique à une température supérieure à 400°C. On effectue l’hypothèse que ces dates sont contemporaines de la date de fin d’activité. On sait construire des lois a priori sur l’âge qui respectent la contrainte de contemporanéité des matériaux datés et de l’évènement d’intérêt. Par la formule de Bayes, on peut alors calculer la loi a posteriori à partir des mesures en laboratoire sur les objets et la loi a priori qui lie l’âge des objets avec celui de l’évènement d’intérêt. Cette loi permet ensuite de calculer un intervalle de crédibilité pour la date recherchée.

 
Les dates d’éruption d’un volcan

En utilisant le carbone 14, on peut dater une éruption volcanique. Comme pour l’exemple de l’atelier de poterie, on ne date pas directement l’éruption : on suppose qu’elle est contemporaine de l’âge de mort des végétaux trouvés dans la couche de lave associée à cette éruption. Une telle approche fournit une date pour chacune des couches. La statistique bayésienne va permettre d’introduire une information a priori supplémentaire en prenant en compte la stratigraphie. Les couches supérieures étant plus jeunes, on peut imposer une contrainte d’ordre sur les âges en fonction de la profondeur de la couche de lave. Cette contrainte est imposée grâce à la loi a priori qui donne une probabilité nulle à tous les âges qui ne vérifient pas la contrainte d’ordre. La loi a priori ainsi construite et les datations par ¹⁴C sur les végétaux génèrent une loi a posteriori qui permettra d’obtenir une estimation plus précise des âges.

La statistique bayésienne permet ainsi d’intégrer des informations complémentaires aux mesures fournies par les laboratoires de datation. On peut ainsi estimer l’âge d’évènements non directement mesurables en laboratoire et imposer des contraintes pour améliorer la précision de l’estimation.