
Les mathématiques naquirent il y a bien longtemps : à peine sut-on compter, il fallut bien leur donner des noms. Puis on les écrivit. La première trace de numération au monde date d’il y a vingt mille ans et fut découverte dans les années 1950 dans l’actuelle République démocratique du Congo : ce sont les os d’Ishango, longs d’environ dix centimètres. On y voit apparaître des groupes d’entailles qui sont certainement une représentation numérique, un peu à la manière de ce que faisaient les Romains en notant « III » pour symboliser le nombre trois.
À cette époque, les nombres servaient à compter, à dénombrer : des personnes, des bêtes, des jours. Au IVe siècle avant notre ère, Platon écrivait en effet dans le Timée que nous avons inventé les nombres en constatant la répétition du jour et de la nuit, de l’hiver et du printemps. Il en déduit que les nombres n’existent dans notre esprit que parce que nous sommes doués de sens, en particulier de la vue, qui nous permet de remarquer ces répétitions. Les nombres sont donc nés comme des objets sensibles servant à caractériser d’autres objets par le biais de leur quantité.
Pythagore et son école
Les Grecs ont toujours admiré leurs prédécesseurs : Égyptiens, Babyloniens et Phéniciens avaient en effet développé de grandes compétences dans l’art du calcul appliqué aux nombres et aux figures géométriques. Les Phéniciens en avaient besoin pour leurs calculs commerciaux, les Babyloniens pour établir des calendriers, les Égyptiens pour calculer les taxes à payer au pharaon sur les surfaces cultivables. C’est ainsi, aux dires d’Hérodote (dans Histoires, vers –445), qu’est née la géométrie : lorsque le Nil débordait sur un champ, le paysan ne devait pas payer de taxes pour la surface immergée. Les Égyptiens se sont ainsi intéressés aux fractions de l’unité – la part d’un tout –, au point qu’on appelle aujourd’hui fractions égyptiennes les nombres de la forme 1/2, 1/3, 1/4, 1/5…, dont le numérateur est égal à 1.
Un jour, un homme originaire d’une petite île grecque au large de l’actuelle Turquie alla voyager en Égypte pour s’y former en mathématiques et en philosophie auprès des prêtres. L’Égypte ayant été conquise par les Perses, il fut emmené bon gré mal gré à Babylone et en profita pour parfaire son apprentissage. Revenu chez lui après une bonne vingtaine d’années de ce que l’on appellerait aujourd’hui un Erasmus, il migra une fois encore pour se fixer définitivement en Italie du Sud. Cet homme, c’est Pythagore de Samos, le Pythagore dont on apprend dès le collège un théorème qui porte son nom mais qu’il a lui-même appris des Égyptiens et n’aurait jamais eu le culot de considérer comme étant sa propre découverte.
Lorsqu’il se fixe à Crotone, dans l’actuelle Calabre, il y fonde son école philosophique et diffuse une pensée qui est sans doute la plus retentissante de l’histoire de la philosophie et des mathématiques. Si son influence sera déterminante notamment pour Platon, Galilée ou encore la plupart des livres de vulgarisation mathématique contemporains, c’est parce qu’il développe une philosophie du nombre jusqu’alors inédite. « Tout est nombre » entend-on souvent dans la bouche de Pythagore. En réalité, il n’a pas dit cela mais une chose bien plus subtile, qui nous est expliquée par Théano, son épouse, dans un ouvrage intitulé De la piété et dont on n’a conservé que de rares extraits, dont celui-ci :
« Je me suis laissé dire que beaucoup de Grecs pensaient qu’à en croire Pythagore tout naît du Nombre. Voilà un discours qui pose une difficulté : comment concevoir que ce qui n’a pas d’existence puisse en même temps engendrer ? En fait, Pythagore n’a pas dit que tout est produit à partir du Nombre, mais que tout était formé conformément au Nombre car l’ordre originel est dans le Nombre et que c’est par participation [à cet ordre] que les choses qui peuvent être nombrées sont placées comme première, deuxième
et ainsi de suite. »
Pythagore voit en le concept « Nombre », qui prend désormais une capitale, l’ADN de toute chose : la logique de création et d’existence du monde est la même que celle du nombre. Cela ne signifie pas que chacun de nous soit un nombre, mais que tout ce qui nous constitue est fondé sur une architecture identique à celle des nombres. C’est d’après cette philosophie que Platon, sous l’influence de son ami pythagoricien Archytas de Tarente, imagina plus tard le monde des Idées dans lequel il existe, par exemple, une « chaise parfaite », qui est le modèle de toutes les chaises, et dont nous ne pouvons construire que de pâles imitations. De la même manière, le Nombre, pour Pythagore, est l’essence du monde. C’est ainsi qu’il devient digne d’intérêt non plus pour compter des objets mais pour ses propriétés intrinsèques.
Les philosophes-mathématiciens d’influence pythagoricienne, comme Philolaos de Crotone, Hippase de Métaponte, Théodore de Cyrène ou Archytas de Tarente (entre – 500 et – 300), puis néopythagoricienne, tels Nicomaque de Gérase, Porphyre de Tyr, Jamblique de Chalcis ou Boèce (entre + 100 et + 500) vont donc tous chercher les propriétés des nombres en lien avec des notions philosophiques, voire parfois magiques.
La représentation géométrique des nombres fut un grand axe de recherches : les nombres triangulaires (dont la représentation du nombre 10, sous la forme de la tetraktys) furent très étudiés, tout comme les nombres carrés, les nombres pentagonaux… Si les nombres triangulaires permettent facilement de démontrer que la somme des n premiers entiers vaut
(p – 1)-gone d’ordre n et un triangle d’ordre n – 1, comme on peut le lire dans le tableau ci-après (par exemple, 66 = 51 + 15).

Les quatre premiers nombres triangulaires.
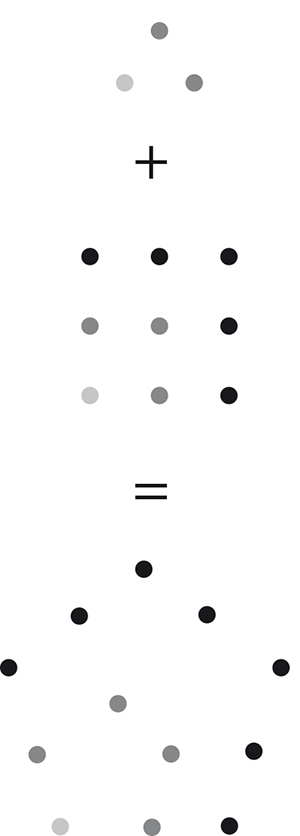
Décomposition d’un nombre pentagonal.
Une vaine beauté
À quoi cela peut-il bien servir ? Sans doute à rien, et c’est toute la révolution pythagoricienne : on étudie le nombre pour ses propriétés intrinsèques, sans même avoir besoin de chercher une application. Il en existe néanmoins une : Fermat conjectura que tout nombre entier positif pouvait se décomposer en au plus p nombres p-gonaux. Lagrange en démontra le cas particulier p = 4, qui n’est autre que le fameux théorème des quatre carrés (tout entier peut s’écrire comme somme de quatre carrés ; voir le dossier « Lagrange » dans Tangente 151, 2013).
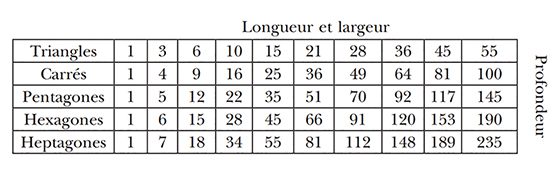
Les nombres et leurs puissances.
Une autre propriété fort sympathique est la décomposition des carrés et des cubes en nombres impairs :
12 = 1,
22 = 1 + 3,
32 = 1 + 3 + 5,
42 = 1 + 3 + 5 + 7,
52 = 1 + 3 + 5 + 7 + 9, etc.
De même :
13 = 1,
23 = 3 + 5,
33 = 7 + 9 + 11,
43 = 13 + 15 + 17 + 19,
52 = 21 + 23 + 25 + 27 + 29, etc.
De ces deux propriétés, on peut déduire, avec un peu d’astuce, le théorème de Nicomaque :
13 + 23 + 33 + … + n3 = (1 + 2 + 3 + … + n)2.
À quoi tout cela sert-il ? On trouvera sans difficulté quelques applications pratiques, mais la meilleure réponse serait « à rien », car c’est justement le sens du Nombre depuis Pythagore : une vaine beauté et son inutilité est la plus grande de ses qualités.
[encadre]
Une nouvelle saga : les grands moments des mathématiques
L’histoire des sciences avance en général dans la continuité. Pourtant, à certains moments privilégiés apparaît une théorie ou une approche novatrice qui bouleverse la vision d’un domaine des mathématiques. Ce fut le cas de la théorie de Galois ou de l’introduction des coordonnées cartésiennes en géométrie.
Un ou deux savants exceptionnels sont souvent les acteurs de ces changements, mais leur rôle ne suffit pas toujours. Parfois, il est important que certaines conditions propices à ces bouleversements soient réunies. Un monde scientifique suffisamment réceptif est, par exemple, un bon début. Ainsi le Discours de la méthode de Descartes n’est-il pas arrivé par hasard dans le Grand Siècle. A contrario, Aristarque de Samos a proposé un système héliocentrique… que personne n’a su reconnaître à son époque. De même, l’introduction précoce du zéro par Jamblique au début du IIIe siècle n’a pas connu de suite car sa vision purement arithmétique du oudên (« rien ») n’était pas accompagnée d’un discours philosophique.
La « saga des grands moments » s’attachera à décrypter ces épisodes privilégiés, et, tout en présentant les acteurs, à analyser dans quelles conditions ils ont pu se produire et quelles conséquences ils ont eues sur le développement des mathématiques. On y retrouvera l’introduction de l’algèbre, la naissance de la logique formelle, ou encore l’apparition des géométries non euclidiennes.
À tout seigneur, tout honneur : dans l’Antiquité, Pythagore fut le précurseur d’une nouvelle vision de l’Univers, plaçant le nombre au centre d’une conception philosophique de l’ordre du monde.
[/encadre]
Lire la suite