Un millésime qui parle de lui-même
Ivan Niven publia en 1977 un article sur les nombres qui portent désormais son nom et qui, comme 2020, sont divisibles par la somme de leurs chiffres. En base 10, 2020 est un nombre de Niven ( on dit aussi nombre Harshad ) car 2 + 0 + 2 + 0 = 4 et 2020 = 4 × 505.
Découvrez quelques propriétés de ces entiers à la page Problèmes « Les nombres autobiographiques ».
L’architecte et designer américain Buckminster Fuller qualifiait en 1979 (dans Synergetics, aux éditions MacMillan) de nombres de Shéhérazade les entiers palindromes, et aurait pu écrire 2020 comme un palindrome autoréférent en base 100. En effet, 2020 = 20 × 100 + 20 et s’écrit donc 2020100. Dans le même état d’esprit, 2020 est un nombre autodescriptif : il s’écrit à l’aide de deux 0, de zéro 1, de deux 2 et de zéro 3. Plus généralement, John Horton Conway a défini en 1986 les suites audioactives (voir la première partie de notre dossier sur l’autoréférence, parue dans notre dernier numéro).

Commencer l’année en douceur
Les facteurs premiers de 2020 sont tous « petits », ce qui permet en guise d’échauffement de dépoussiérer le vénérable crible d’Ératosthène et d’obtenir la factorisation
2020 = 2 2 × 5 × 101.
Faisons un bond de près de deux mille vingt ans. En 1640, Pierre de Fermat obtient une caractérisation des entiers qui peuvent s’écrire comme somme de deux carrés : il s’agit de ceux dont les facteurs premiers de la forme 4k + 3 apparaissent avec une puissance paire dans la décomposition. Comme 2020 ne possède pas de facteurs premiers de cette forme, une telle décomposition existe. On en trouve même deux :
16 2 + 42 2 et 24 2 + 38 2.
En 1742, Christian Goldbach formula « sa » conjecture, qui résiste toujours, selon laquelle tout entier pair est somme de deux nombres premiers. Avec 2020, on obtient quarante et une telles décompositions : 3 + 2017, 17 + 2003, 29 + 1991…
D’après le théorème de Lagrange, énoncé (et démontré, lui) au XVIIIe siècle, tout entier est somme de quatre carrés. Ainsi, après quelques tâtonnements en attendant le réveillon, on a trouvé 2020 = 2 2 + 4 2 + 8 2 + 44 2.
Deux carrés, quatre carrés… Et avec trois ? Gustav Lejeune-Dirichlet a démontré en 1857 que tout entier positif ne s’écrivant pas 4 p (8q + 7) avec p et q deux entiers est somme de trois carrés. C’est le cas pour 2020, qui peut ainsi s’écrire 18 2 + 36 2 + 20 2.
Magie arithmétique !
Le Finlandais Mikko Harju a trouvé cette égalité suite à un défi lancé par Alex Bellos :
10 × 9 × 8 + (7 + 6) × 5 × 4 × (3 + 2) × 1 = 2020.
À l’occasion d’une exposition à la Fondation Cartier à Paris en 2011–2012 (voir Tangente 143), Takeshi Kitano avait imaginé d’écrire les entiers en utilisant successivement 1, 2, 3… et les symboles arithmétiques. On rappelle que la factorielle n! de l’entier n désigne le produit des entiers de 1 à n. Ainsi, 4! = 1×2×3×4 = 24.
Avec la règle de Kitano, 2020 s’écrit, à volonté, avec les huit premiers entiers :
1 + 2 – 3×(4! + 5 – 6!) – 7×8 (Alain Zalmanski), ou avec les sept premiers :
(1 + 2)!! + (3!) 4 + 5 + 6 – 7 (Jean-Louis Legrand). On peut cependant faire mieux avec les six premiers entiers seulement, en écrivant –12 + 3! 4 + 5 + 6! (Élisabeth Busser), ou encore
1 – 2 + (3!) 4 + 5 + 6! (Hervé Lehning et François Lavallou). Record à battre ?
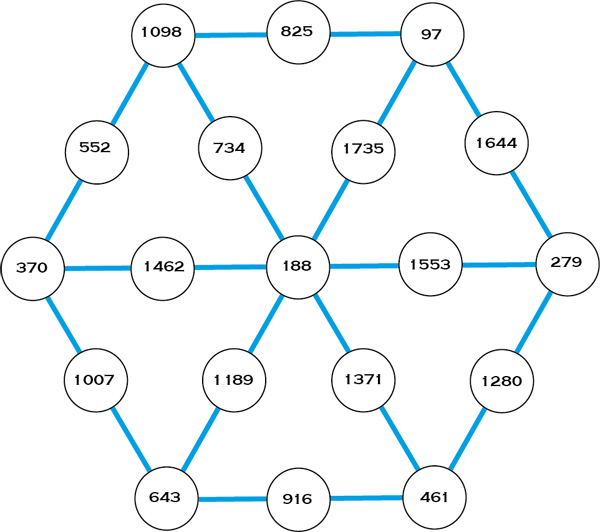
Le mathémagicien Dominique Souder, dont les ouvrages de référence sont désormais disponibles au format ePub sur les plateformes numériques, fête l’arrivée de 2020 à sa façon, avec cet hexagone magique, où l’on retrouve 2020 dans chacun des douze alignements.
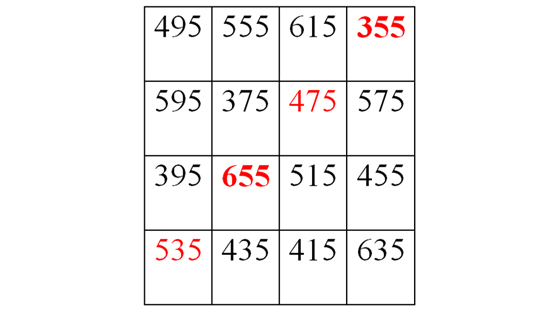
Alain Zalmanski fait de 2020 une année carrément magique, nous demandant aussi de ne pas oublier la date palindromique 02–02–2020 (très rare !). Au fait, saurez-vous retrouver au moins quarante-huit fois (d’après F. Lavallou) le nouveau millésime sur son carré magique ?