
Au départ, ce n’est qu’une devinette posée en marge des Olympiades internationales de mathématiques de 1977, qui se tiennent alors à Belgrade en Yougoslavie. Mais son origine est, peut-être, plus ancienne. Voilà le problème tel qu’il a été posé :
1,
11,
21,
1211,
111221,
312211.
Quelle est la ligne suivante ?
Que voit-on sur la première ligne ? On voit un « 1 » : en concaténant ces deux chiffres que l’on lit, cela constitue la deuxième ligne. Sur cette ligne, que trouve-t-on ? On voit deux « 1 », soit les deux chiffres qui figurent sur la troisième ligne. Sur celle-ci, on voit un « 2 » et un « 1 », soit les chiffres de la quatrième ligne. Et ainsi de suite, chaque ligne décrivant la liste des nombres qui se trouvent, dans cet ordre, sur la ligne précédente. On peut ainsi donner la septième ligne, celle qui est demandée : 13112221. La devinette est résolue.
Prenez-en de la graine
On pourrait croire que c’est fini. Mais pas pour des esprits curieux, surtout quand on s’appelle John Horton Conway ! Ce célèbre mathématicien britannique, né en 1937, était à l’époque professeur à l’université de Cambridge.
Le processus précédent peut se poursuivre, pour construire une suite dont les termes sont les lignes successives : 1, 11, 21, 1211, 111221, 312211, 13112221, 1113213211… Le premier terme, ici 1, s’appelle la graine. En prenant 191 comme graine, on obtient :
191,
111911,
311921,
1321191211,
1113122119111221,
…
On obtient la suite 191, 111911, 311921, 1321191211, 1113122119111221…
Toutes les suites construites de cette manière s’appellent des suites look and say (en français, « regarde et dis »). On parle aussi de suites audioactives (voir plus loin la raison de cette terminologie). Ce sont toutes ces suites que John Conway a étudiées.
Mis à part la suite stationnaire dont la graine est 22, la longueur de chacun des termes successifs d’une suite audioactive donnée augmente au fur et à mesure que l’on progresse. Peut-on mesurer cette augmentation ? La réponse est oui et le taux d’accroissement tend vers 30,36 % quand on progresse dans la suite (voir encadré).
[encadre]
Problème bête, nombre compliqué
Si l’on appelle Ln la longueur du terme de rang n d’une suite audioactive, le rapport Ln / Ln–1 tend vers une limite finie λ quand n tend vers l’infini. Cette valeur est la même quelle que soit la graine (hormis 22, bien sûr !) et une valeur approchée à 10–4 près en est 1,3036. En fait, λ, que l’on appelle la constante de Conway, est la seule racine réelle positive d’un polynôme de degré 71. Représentons, dans le plan complexe, les soixante et onze racines de ce polynôme.
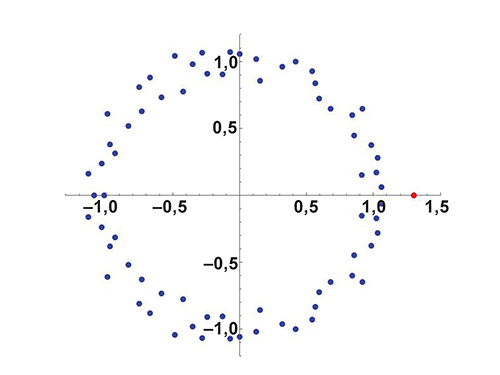
En plus de λ (en rouge), ce polynôme possède deux racines réelles négatives (en bleu, sur l’axe des abscisses) ; toutes les autres racines sont complexes non réelles. Comme le polynôme est à coefficients entiers, λ est un nombre algébrique. Mais il ne peut pas s’exprimer à l’aide de sommes, produits, différences, divisions et extractions de racines énièmes d’entiers. En 1997, John Conway écrivait alors que λ détient sans doute le record du nombre algébrique le plus compliqué provenant d’un des problèmes les plus bêtes !
[/encadre]
On peut s’intéresser aussi aux suites audioactives d’un point de vue qualitatif. Conway a adopté une terminologie imagée : il a appelé descendants tous les termes qui suivent la graine. Puis il dit que le premier est âgé d’un jour, le deuxième est âgé de deux jours et ainsi de suite. Alors, selon le théorème du deuxième jour, aucun chiffre d ≥ 4 ne peut naître après le deuxième jour. Faites des expériences, à partir des graines 191, 1111 ou autres : si un chiffre d ≥ 4 apparaît, c’est qu’il est déjà présent soit dans la graine, soit à la deuxième étape. Essayons de comprendre ce phénomène. Prenons l’exemple 1111, 41, 1411, 111421, 31141211, 132114111221, 1113122114312211… À partir du descendant du deuxième jour, le 4 continue de vivre mais aucun autre chiffre 4 n’apparaît. De plus, la sous-chaîne de gauche se terminant par 4 n’interagit plus avec la sous-chaîne de droite, qui ne commencera jamais par 4. Ces deux sous-chaînes vont « vivre de manière indépendante ». Cela n’est pas lié à la présence du 4. Par exemple, reprenons la suite initiale et séparons la huitième ligne « 1113213211 » en deux parties « 11132.13211 », puis continuons le processus:
11132.13211, 311312.11131221, 1321131112.3113112211, 11131221133112.132113212221…
On constate à nouveau que la sous-chaîne de gauche qui se terminera toujours par 2 n’interagit plus avec la sous-chaîne de droite qui commencera toujours par 1 ou 3. Une scission s’est produite et le processus se poursuit : les sous-chaînes obtenues peuvent, elles aussi, se scinder les jours suivants, donnant alors de nombreuses sous-chaînes. Mais ce phénomène a une fin car il existe des sous-chaînes qui ne peuvent pas se scinder et elles apparaissent un jour parmi les descendants. Cela étant, il n’y a plus d’interaction entre toutes ces sous-chaînes, qui évoluent alors de manière indépendante. John Conway les a toutes déterminées : il les a appelées éléments communs.
Une arithmétique chimique
Ce qui est remarquable est que les éléments communs sont en nombre fini : il y en a exactement 92. Par analogie avec les éléments chimiques du tableau périodique de Mendeleïev, Conway, avec un humour très particulier, leur a donné les noms des éléments chimiques. Ainsi, 22 est l’hydrogène (H), de numéro atomique 1, 131112 est le cuivre (Cu), de numéro atomique 29, 111311222112 est le manganèse (Mn), de numéro atomique 25, 3 est l’uranium (U), de numéro atomique 92… Seul l’hydrogène est stable (22 conduit à 22). Les autres éléments ont une descendance, c’est-à-dire qu’ils se « désintègrent », d’où le nom de « suite audioactive », par analogie avec les éléments chimiques radioactifs. Ainsi, pour les amateurs de cette arithmétique chimique, le cuivre (Cu) se désintègre en nickel (Ni) : 131112 donne 11133112, et le manganèse se désintègre en un composé chrome–silicium (Cr-Si) via 111311222112
À côté de ces éléments communs, en présence de chiffres d ≥ 4, il existe deux autres familles, appelées par Conway éléments transuraniens car situés après l’uranium dans la table, donc de numéros atomiques 93 et 94. Ce sont le neptunium Np = 1311222113321132211221121332211d avec d un chiffre supérieur à 4 et le plutonium Pu = 31221132221222112112322211d avec à nouveau d un chiffre supérieur à 4. Il en existe donc plusieurs isotopes selon la valeur du chiffre d. Remarquez que le plutonium se désintègre en neptunium…
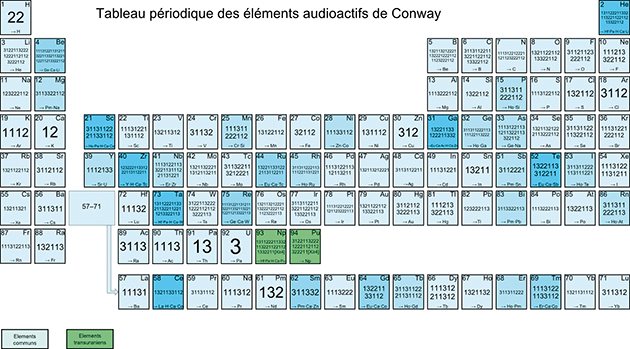
Si l’on part de la graine 3 (uranium, de numéro 92), on obtient tous les éléments communs du tableau, dans l’ordre décroissant de leur numéro atomique. Cette suite look and say particulière a été nommée par le mathématicien canadien Ilan Vardi suite de Conway.
Un théorème cosmologique
À partir de cette classification, on a le résultat suivant, appelé par Conway théorème chimique : quand la graine est un élément commun, alors tous ses descendants sont des composés d’éléments communs. De plus, si la graine n’est pas l’élément stable H = 22, alors, à partir d’un certain nombre de jours, tous les descendants sont des composés faisant intervenir, pour chacun d’entre eux, tous les éléments communs. Et si un descendant contient un élément transuranique, alors tous les suivants contiendront un élément transuranique.
Il existe des éléments qui ne sont ni communs, ni transuraniques, c’est-à-dire qu’ils n’appartiennent pas au tableau des éléments audioactifs. C’est le cas, par exemple, de la graine 1 et de ses premiers descendants : 1, 11, 21, 1211, 111221, 312211, 13112221. Ces éléments sont appelés exotiques. Ils sont en nombre infini.
Dans le cas de la suite de graine 1, à partir du septième jour, on retrouve un composé d’éléments communs, soit 1113213211 = Hf-Sn, composé d’hafnium (Hf) et d’étain (Sn), de numéros atomiques 72 et 50. En vertu du théorème chimique, tous les descendants âgés de plus de sept jours ne contiennent alors que des éléments communs : il n’y a plus d’élément exotique !
En fait, ce qui est vraiment remarquable, c’est que ce résultat est général pour toutes les suites audioactives en vertu du théorème le plus important de cette étude, le théorème cosmologique, appelé aussi théorème du vingt-quatrième jour : pour toutes les suites look and say (c’est-à-dire quelle que soit la graine), à partir du vingt-quatrième jour, les descendants sont tous des composés d’éléments communs et d’éléments transuraniques.
En vertu de ce théorème, à partir du vingt-quatrième jour, les éléments exotiques ont tous disparu ! La démonstration de ce résultat est due à John Conway et Richard Parker (l’un de ses collaborateurs à Cambridge). Elle consiste, par des arguments subtils, à ramener le problème à l’examen de quelques centaines de cas… mais les pages manuscrites ont été perdues ! Une deuxième démonstration est due à Michael Guy, mais elle a été perdue aussi…
Il reste de cette deuxième démonstration l’existence d’un élément exotique, le methuselum (Me = 2233322211davec d ≥ 4), nécessite réellement vingt-quatre jours pour voir disparaître tous ses éléments exotiques dans ses descendants. La borne des vingt-quatre jours est donc bien la meilleure possible. Le lecteur courageux pourra écrire les vingt-quatre descendants de Me et vérifier, ce qui est très long, la disparition de tous les éléments exotiques.
Il faudra attendre 1997 pour voir une démonstration du théorème cosmologique. Elle est due à Shalosh B. Ehkad et Doron Zeilberger. Le premier auteur est en fait… l’ordinateur du second auteur, qui lui est un (vrai) mathématicien, Israélo-Américain né en 1950 enseignant à l’université Rutgers dans le New Jersey (États-Unis). Ils prouvent en fait le théorème avec une borne de vingt-neuf jours. En 2003, enfin, Richard Litherland, de l’université d’État de Louisiane (États-Unis), prouve le théorème avec la borne des vingt-quatre jours.
Les lecteurs qui ont découvert cette innocente devinette dans le roman le Jour des fourmis de Bernard Werber (Albin Michel, 1992) n’imaginent sans doute pas le paysage arithmético-chimique merveilleux qui se cache derrière la porte…
[encadre]
Les nombres autoaudioactifs
Un nombre autoaudioactif, appelé aussi autodescriptif, est un entier N défini de la manière suivante : dans l’ordre naturel des chiffres de 0 à 9, on trouve dans l’écriture de N le nombre d’occurrences du chiffre d, puis le chiffre d lui-même (pour d = 0, 1, 2… 9). Ainsi, dans le nombre N1 = 10 213 223, il y a un chiffre « 0 », deux chiffres « 1 », trois chiffres « 2 » et deux chiffres « 3 ». On obtient bien N1 en concaténant 10, 21, 32 et 23.
Dans N2 = 101 112 213 141 516 171 819, on a un chiffre « 0 », onze chiffres « 1 », deux chiffres « 2 », un chiffre « 3 », et de même pour les chiffres de 4 à 9. N2 résulte précisément de la concaténation des éléments de cette description (10, 111, 22, 13, 14, 15, 16, 17, 18, 19).
Il n’y a qu’un nombre fini de nombres autoaudioactifs, 109 au total. Les premiers sont 22, 10 213 223, 10 213 233, 10 313 314, 10 313 315, 10 313 316, 10 313 317, 10 313 318, 10 313 319, 21 322 314 et 21 322 315. Le plus grand est 101 112 213 141 516 171 819.
[/encadre]
[encadre]
John Conway, la passion du jeu... mathématique
Le touche-à-tout John Conway s’est brillamment illustré dans la théorie des groupes finis, dans les réseaux, dans les polyèdres et les polytopes, dans la théorie des nœuds, dans les jeux et récréations mathématiques, dans le codage, dans la théorie des nombres… Grand joueur de backgammon, il s’est très tôt intéressé aux jeux de stratégie. S’inspirant d’une idée de John von Neumann sur une machine théorique se reproduisant elle-même, il invente le fameux « jeu de la vie », qui le rendra célèbre. En 1986, il part pour les États-Unis, où il occupe la chaire John-von-Neumann à l’université de Princeton ; il y est maintenant professeur émérite.
[/encadre]
Lire la suite