
Le pape de l’autoréférence en littérature est Éric Angelini, que vous retrouverez en page En bref et et dans l'article Jouer avec des nombres. Son site, exhaustif autant que cela peut l’être et autoréférent comme il se doit (cetteadressecomportecinquantesignes.com), est à consulter absolument. Parmi de multiples pépites, on trouve par exemple tous les mots qui, au Scrabble, écrivent leur valeur totale en points (l’indice 0 est celui des jetons blancs utilisés comme joker).

La somme des lettres de chaque mot est la valeur du nombre indiqué par ce mot.
Pour rester dans les jeux de lettres, Frédéric Martin a concocté en 2006 un « carré 69 x 69 autoréférent » qui intéressera les cruciverbistes et les amateurs de Scrabble. Ayant pour total 10 248 horizontalement et verticalement, il comporte 0 fois « ZÉRO », 1 fois « UN », 2 fois « DEUX », 3 fois « TROIS », 4 fois « QUATRE », 5 fois « CINQ »… et 100 fois « CENT » ! Cette grille extraordinaire est évidemment recensée sur le site d’Éric Angelini. Sur son Web log « Journal d’un Terrien », Serge Boisse propose lui aussi une rubrique « Phrases autodescriptives » qui intéressera les amateurs.
[encadre]
Une phrase qui se décrit lettre à lettre
« Ce titre contient quatre “a”, un “b”, cinq “c”, cinq “d”, dix-neuf “e”, deux “f”, un “g”, deux “h”, treize “i”, un “j”, un “k”, un “l”, un “m”, seize “n”, trois “o”, quatre “p”, sept “q”, sept “r”, sept “s”, quinze “t”, dix-huit “u”, un “v”, un “w”, six “x”, un “y” et quatre “z”. »
L’auteur de ce texte, Jacques Pitrat (1934–2019), fut un pionnier de l’informatique, et plus précisément de l’intelligence artificielle symbolique. La programmation amenant la réalisation de cette phrase n’est pas aisée !
[/encadre]
Des chiffres aux fractales
La plupart des systèmes de numération anciens utilisent des chiffres autoréférents. Ainsi, dans le système romain, I, II et III sont autoréférents. Les systèmes de notations des chiffres en notation bâton ( |, ||, |||, ||||…) le sont également. Ils sont par ailleurs un obstacle au progrès : en abandonnant l’autoréférence (sauf pour le 1), les chiffres dits arabes ont amené à une notation plus conceptuelle. Nicolas Graner a concocté un pangramme* autoréférent avec les chiffres romains : IX « I », I « V », II « X »,
I « L », I « C », I « D », I « M ».
La suite fractale 1, 1, 2, 1, 3, 2, 4, 1, 5, 3, 6, 2, 7, 4, 8, 1, 9, 5, 10, 3, 11, 6, 12, 2, 13, 7, 14, 4, 15, 8… se contient elle-même, ce que l’on voit en supprimant un nombre sur deux : en ne conservant que les nombres noirs, on retrouve la même suite infinie. On peut alors recommencer l’opération, autant de fois que voulu (essayez !), sur cette suite qui résulte… d’un battage de cartes (voir « Suites de nombres fractales » sur le site villemin.gerard.free.fr de Gérard Villemin).
Il existe en fait de nombreuses suites fractales (voir Jeux mathématiques et Mathématiques des jeux, de Jean-Paul Delahaye, Bibliothèque Pour La Science, 1998) ! La suite de Thue–Morse ne contient que des « 0 » et des « 1 » : 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0… La suite commence par « 0 » et reste identique à elle-même quand on remplace « 0 » par « 01 » et « 1 » par « 10 ». Cette définition, de proche en proche, permet de connaître toute la suite en partant du seul premier terme « 0 ».
La suite du lézard L, introduite par Éric Angelini, est telle que si l’on prend un terme sur trois on obtient la suite L… mais, en outre, les termes supprimés constituent encore la suite L. C’est la seule suite constituée de « 0 » et de « 1 », commençant par « 0 », possédant cette propriété fractale. La voici :
L = 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1… La suite L se sépare donc naturellement en deux sous-suites par le choix d’un élément (en bleu) sur trois :
0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1…
et 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1…, toutes deux identiques à la suite L initiale. Bravo l’artiste !
Les ensembles de Mandelbrot sont des fractales où certaines parties, comme on peut le voir sur l’illustration (regarder les ensembles noirs en forme de cardioïdes), sont essentiellement identiques au tout. L’étude des parties de l’ensemble n’est donc pas plus facile que celle du tout puisqu’elles leur sont autosimilaires (voir les Fractales, Bibliothèque Tangente 18, 2019). La difficulté de cette étude contredit un précepte énoncé par Descartes qui consiste à « diviser chacune des difficultés […] en autant de parcelles qu’il se pourrait, et qu’il serait requis pour les mieux résoudre ».

Un ensemble de Mandelbrot.
Autopavés et autologlyphes
En 1963, Martin Gardner (1914–2010, voir Tangente 136, 2010) présentait dans le mensuel Scientific American des figures autopavables, à savoir des formes qui, quand on les assemble en plusieurs copies, reconstituent la forme initiale « en plus grand » (voir Mathematical Magic Show, Random House Inc., 1977). L’ingénieur britannique Lee Sallows va plus loin dans On self-tiling tile sets (Mathematics Magazine 85, 2012) et définit les ensembles autopavables comme des ensembles E de plusieurs formes planaires F tels que chaque forme F de l’ensemble E s’obtient « en plus grand » par un assemblage n’utilisant qu’une fois chaque forme de E.
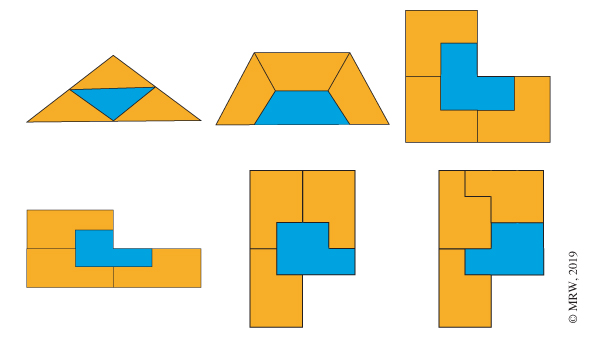
Figures autopavables.
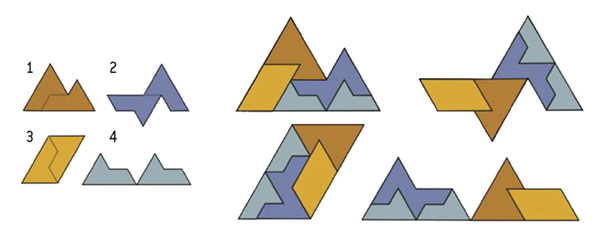
Ensembles autopavables.
Dans les autologlyphes, le dessin rejoint le dessein. Ainsi l’autologlyphe « Cantor » évoque l’ensemble triadique de Cantor, dans lequel on supprime à chaque étape le tiers médian des segments : on enlève le tiers médian d’un segment, puis le tiers médian des deux segments qui restent, et ainsi de suite. Les « poussières » résiduelles qui subsistent après une infinité d’étapes constituent l’ensemble triadique de Cantor (voir les Ensembles, Bibliothèque Tangente 61, 2017). Le graveur Maurits Cornelis Escher (1898–1972) s’est particulièrement illustré dans la représentation d’éléments autoréférents (voir Mathématiques et Arts plastiques, Bibliothèque Tangente 23, 2019).

Autologlyphe évoquant l’ensemble triadique de Cantor.
Les peintures de Magritte et le dessin de Plantu permettent une transition avec l’étape suivante dans l’autoréférence : l’autocontradiction. L’exemple le plus connu dans l’art en est un fameux tableau calligramme de Magritte. Il en existe plusieurs interprétations ; la mieux acceptée est une illustration du principe selon lequel l’image (de la pipe) n’est pas le mot (« pipe »).

La trahison des images, de René Magritte (1929), se trouve au musée Magritte,
à Bruxelles (Belgique).
Un calligramme autocontradictoire, humoristique et déchirant, a été publié par Plantu dans le journal Le Monde, le 3 février 2006, à partir de la phrase : « Je ne dois pas dessiner Mahomet. »

Calligramme autocontradictoire de Plantu.
La logique s’en mêle
L’autoréférence est la source de nombreux paradoxes logiques, dont le calamiteux : « Les Crétois mentent toujours. » Ce dernier aurait été énoncé par Épiménide, Crétois lui-même. Disant cela, l’auteur, qui est un Crétois et doit donc toujours mentir si l’on en croit la phrase, prononce une assertion… fausse, puisqu’il dit la vérité de la phrase. Mais si, en disant cela, il dit la vérité, alors il existe un Crétois qui ne ment pas (en l’occurrence, Épiménide lui-même), et la phrase est fausse. On en conclut que la phrase est indécidable, ce qui a longtemps été insupportable en logique.
La version simplifiée est la phrase « Je mens. », qui est aussi autoréférente et autocontradictoire. Le mathématicien Kurt Gödel a exploité ce phénomène pour montrer qu’on ne pouvait pas toujours prouver qu’un ensemble suffisamment riche d’axiomes ne contenait pas une autocontradiction (voir la Logique, Bibliothèque Tangente 15, 2004). En effet, raisonne Gödel, si un ensemble d’axiomes ne permet de démontrer que des vérités et que l’on puisse écrire la phrase P : « Cette phrase ne peut pas être démontrée avec les axiomes de l’ensemble. », alors cette affirmation P ne peut être démontrée et elle est donc vraie. Il existe donc des affirmations vraies mais indémontrables (voir les Mathématiques de l’impossible, Bibliothèque Tangente 49, 2013), ce qui est insupportable.
De manière similaire, il existe des verbes qui, conjugués à la première personne, comme « je mens », « je dors », « je meurs », sont des autoréférences autocontradictoires.
L’attirance pour les autoréférences amène des conflits sur lesquels les paradoxes joueraient simultanément un rôle de détonateur (en exacerbant les oppositions manichéennes) et d’extincteur (en les relativisant). D’inspiration libertaire, la dérision liée à certaines phrases autoréférentes montre qu’un système de valeurs doit se disqualifier lui-même pour s’affirmer. Le drapeau noir se mange lui-même et c’est pourquoi des slogans libertaires sont de nature paradoxale (voir Mathématiques et Philosophie, Bibliothèque Tangente 38, 2019) : « Seul mot d’ordre : aucun mot d’ordre ! », « Enfin un T-shirt où il n’y a rien d’écrit » (inscription sur un T-shirt) ou le célèbre « Il est interdit d’interdire ».
Certaines injonctions autoréférentes sont impossibles : essayez de donner comme gage à quelqu’un « Pour guérir de votre obsession, faites trois fois le tour du pâté de maison sans penser au mot “dinosaure” »… L’école de psychanalyse de Palo Alto, sous l’instigation de Paul Watzlawick (1921–2007), a montré que l’ordre « Soyez spontané ! » constitue une injonction paradoxale résultant d’une illusion éducative : être spontané ne s’impose ni ne s’improvise. On a pourtant ouvert, à l’intention des acteurs, des écoles d’improvisation et l’on s’interroge : le jour de l’examen, le cancre doit-il improviser, ou montrer ce qu’il a appris ?
Selon ces psychanalystes, les phrases autoréférentes du type « Désobéis-moi ! » ou « Soyez naturel » troublent certains patients, qui voient dans ces consignes stupides des obstacles insurmontables à une vie « normale ». Tout comme l’élève que la consigne de « bien lire » empêche de lire avec attention et intérêt. L’auteur en sait quelque chose…
Connaissance de soi et paradoxes partagent les dangers de l’autoréférence. « Je fais toutes les nuits le même rêve étrange » expliquait le philosophe chinois Tchouang-Tseu, « je me prends pour un papillon léger volant dans l’air azuré, mais, au petit matin, je me retrouve dans la peau d’un homme. Qui suis-je vraiment ? Un homme rêvant la nuit qu’il est un papillon, ou un papillon rêvant le jour qu’il est un homme ? »
Il existe aussi des autocontradictions bénéfiques : d’après Niels Bohr (1885–1962), cité par le physicien Anatole Abragam, il y a une grande différence entre une vérité triviale et une vérité profonde. Une vérité triviale est une affirmation dont l’opposé est faux ; une vérité profonde est une affirmation dont l’opposé est aussi une vérité profonde. L’autoréférence est là : cette définition est-elle une vérité profonde ? Niels Bohr, évoquant ensuite le caractère exécrable de leur collègue Wolfgang Pauli (1900–1958), conclut : « Fondamentalement, Pauli était un homme modeste. » « Vérité profonde ! » répondit Abragam.
Tous ces paradoxes sont-ils légers ou graves ? Chez Russell et Gödel, ils sont graves, et comme tels, sources d’inspiration féconde en logique. Pour beaucoup, ce ne sont que des facéties, tout de même surprenantes. Il reste qu’il est bon d’explorer les raisons d’une surprise.

Lire la suite