Des creux et des bosses

Le physicien tâche souvent de minimiser une énergie, l’économiste un coût, l’ingénieur une qualité et le marchand un chiffre d’affaires. Toutes ces situations ont en général en commun de se décrire par une fonction réelle de plusieurs variables, qu’il s’agit d’optimiser. Il s’agit d’une fonction  f qui, pour chaque valeur d’un ensemble de paramètres x₁, x ₂, x ₃… x _n, renvoie un nombre noté  f (x₁, x ₂, x ₃… x _n) qui correspond à ce qu’il s’agit d’optimiser. Tout l’enjeu est alors de déterminer les valeurs des paramètres pour lesquelles  f (x₁, x ₂, x ₃… x _n) est minimale (ou maximale, selon le contexte).

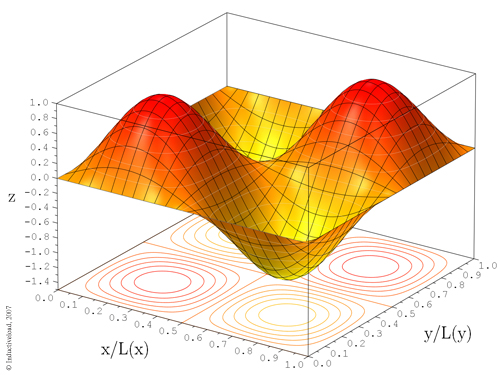
Graphe représentatif d’une fonction de n = 2 variables.

Un problème universel

Posée de façon aussi générale, une telle situation est bien trop vaste pour être traitée en totalité. On peut même dire, avec Euler, qu’elle englobe l’entièreté de la réalité du monde, « car puisque la structure de l’univers est la plus parfaite, et qu’elle est l’œuvre d’un très sage Créateur, rien ne s’y passe sans qu’y apparaisse quelque relation de minimum et de maximum ».

Sans entrer dans les détails techniques, on pourra supposer ici que la fonction  f est « suffisamment régulière », c’est-à-dire que son comportement peut se décrire par un recours à un dessin où tout est « assez lisse », « sans aspérité ». Dans le cas de deux paramètres, x₁ et x ₂, il est possible de donner à voir un graphe représentatif de  f , qui prend la forme d’une surface S. Les deux paramètres y sont un peu comme des longitudes et latitudes sur une carte, la valeur prise par  f étant représentée par une altitude.

Trouver le maximum ou le minimum de  f , c’est donc trouver le plus haut sommet des montagnes ou le point le plus profond. Quitte à remplacer  f  par – f , c’est-à-dire à remplacer les creux par des bosses et inversement, on peut toujours supposer que ce qui nous intéresse est la détermination d’un minimum.

Dans le cas d’un seul paramètre, c’est-à-dire pour une fonction  f d’une seule variable réelle, le point où le minimum est atteint a pour propriété que la tangente est horizontale (voir article « La dérivée pour toucher le fond ») : localiser les points de la courbe pour lesquels cette propriété est satisfaite permet donc de réduire considérablement la recherche.

Pour utiliser cette même idée dans le cas de fonctions à plusieurs variables, il convient d’abord de généraliser la notion de tangente. Dans le cas de notre fonction  f à deux variables, il nous faut parler de plan tangent à  f en un point. Comme pour une courbe, on peut avoir recours à un zoom autour du point qui nous intéresse. Songeons que la Terre, à notre petite échelle humaine, nous apparaît plate alors qu’elle ne l’est pas : au point où nous sommes, nous confondons la Terre avec un plan tangent, c’est-à-dire le plan qui « colle » le mieux à la forme de la Terre à notre voisinage immédiat.

L’autre manière de voir la tangente à une courbe au point A, plus « dynamique », consistait à dire (toujours dans article « La dérivée pour toucher le fond ») qu’il s’agit de la droite passant par A et orientée selon la direction suivie par un véhicule qui, suivant la route jusqu’en A, glisserait en A sur une plaque de verglas, l’obligeant soudain à se diriger résolument tout droit. Ici, puisque l’on cherche un plan, on peut s’appuyer sur l’idée précédente pour trouver deux directions qui, ensemble, définissent (avec le point A) le plan tangent à la courbe en A.

Pour trouver ces deux directions, coupons S selon deux plans. Le premier est le plan défini par l’ensemble des points dont la première coordonnée est la même que celle de A. C’est un plan vertical, parallèle à l’axe (O x ₂ ), et qui contient bien sûr le point A lui-même. Ce plan coupe S selon une courbe C.

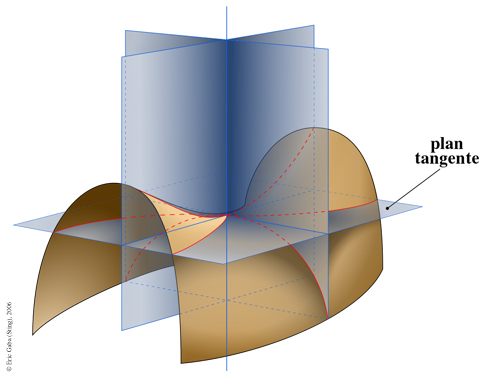
Section de S selon deux plans (verticaux).

Avec C maintenant définie, le cadre est connu : on sait définir la notion de tangente. La direction de cette tangente à C au point A, quantifiée par son coefficient directeur, est la dérivée partielle de  f selon x ₂ (c’est bien x ₂ et non x ₁, car dans le plan de coupe c’est x ₂ qui sert de variable, et non x ₁, qui reste constant). On la note ∂ f / ∂ x ₂.

Couper pour trouver un plan

De la même manière, un second plan de coupe vertical et orienté selon (O x ₁) nous donne une autre dérivée partielle, notée comme on s’y attend ∂ f / ∂ x ₁.

Les deux tangentes obtenues sur les plans de coupes sont deux droites distinctes et qui passent toutes deux par le point A. Ensemble, elles définissent notre plan tangent.

Là, une question vient à l’esprit : si l’on coupe S selon un plan vertical orienté autrement que les deux premiers, alors on obtient une nouvelle courbe, de laquelle se déduit une nouvelle tangente en A. Il serait bien embêtant que celle-ci ne soit pas incluse dans le plan tangent ! Qu’est-ce qui nous garantit que ce problème ne se produira pas ? Eh bien… un théorème.

On peut démontrer en effet que, quelle que soit la route sur S suivie par notre véhicule, au moment où il atteint A et se met à glisser sans plus pouvoir contrôler sa direction, il suit une ligne droite nécessairement incluse dans le plan tangent.

S’il est un peu plus compliqué de définir le plan tangent à une surface que la droite tangente à une courbe, cela tient donc davantage au fait qu’il s’agit d’un plan qu’à la question de la tangence elle-même, qui au fond se traite de façon assez voisine.

Venons-en au minimum de notre fonction f . Là encore, on peut s’inspirer du cas des fonctions et remarquer qu’au point le plus bas de la surface le plan tangent est horizontal.

Au-delà de l’horizontale

Un point de la surface où le plan tangent est horizontal est-il nécessairement un minimum de  f ? Non, bien sûr, ne serait-ce que parce qu’il peut aussi s’agir d’un maximum. C’est pour trancher entre les différentes possibilités que les choses deviennent un peu plus compliquées dans le cas des surfaces, et que la nécessité d’un formalisme plus précis devient difficile à contourner.

En s’inspirant de ce qui a été vu pour les courbes, on peut essayer l’idée suivante : regardons chacune des deux courbes obtenues par nos deux plans de coupes verticaux orientés selon les axes (O x ₁) et (O x ₂). Sur chacune d’elles, identifions si le point A est un minimum, un maximum ou un point d’inflexion. Pour que A soit un minimum de  f , il est nécessaire qu’il soit un minimum sur les deux courbes simultanément. De même pour un maximum, d’ailleurs. Cela permet donc d’affiner encore, et à peu de frais, la liste des points qui atteignent potentiellement un minimum.

En revanche, rien ne dit que cette condition soit suffisante, car il est tout à fait possible d’imaginer qu’en se dirigeant selon une autre direction que (O x ₁) ou (O x ₂) le point A apparaisse comme le maximum d’une courbe plutôt que le minimum, et qu’on ait donc affaire à un point-selle. Un point-selle (ou col) d’une surface S est un point de S qui est un maximum le long d’un plan de coupe vertical et un minimum le long d’un autre plan de coupe. Au voisinage d’un tel point, la surface a alors une forme qui rappelle celle d’une selle de cheval.

Pour en avoir le cœur net, il faut donc approfondir davantage. On pourrait envisager d’étudier l’ensemble des plans de coupe verticaux passant par le point A : si celui-ci est un minimum de toutes les courbes ainsi définies, alors on tient un minimum de  f (même s’il peut n’être que local), et dans le cas contraire on peut écarter A de la liste des candidats. Le problème, c’est qu’on ne va pas se mettre à étudier une infinité de courbes.

Il existe heureusement un moyen pour réduire l’étude. À l’aide d’un outil appelé la seconde forme quadratiquefondamentale, on peut déterminer l’allure de la surface S au voisinage du point A et, en-dehors de cas très spécifiques, déterminer si A est un maximum, un minimum ou un point-selle (voir en encadré).

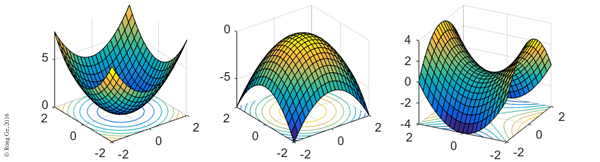
Les trois cas possibles : minimum, maximum et point-selle.

[encadre]

La seconde forme quadratique fondamentale

De façon un peu simplifiée, la seconde forme quadratique fondamentale d’une surface en un point A est la donnée de trois valeurs, notées 
L = ∂ ²f / ∂ x ₁², M = ∂ ²f / ∂ x₁ ∂ x ₂ et N = ∂ ²f / ∂ x ₂². 
Pour calculer L, on dérive deux fois  f selon les règles usuelles en prenant x ₁ comme variable (et en supposant donc x ₂ constant). De même, pour calculer N on dérive deux fois  f en prenant x ₂ comme variable et en fixant x ₁. Enfin, pour calculer M, on dérive une fois  f en prenant x ₁ comme variable, puis le résultat est à son tour dérivé en prenant x ₂comme variable. Pour M, on obtient le même résultat en dérivant d’abord selon x ₂ puis selon x ₁.

La valeur LN – M² (appelée le déterminant de la seconde forme quadratique fondamentale) est la clé qui nous indique ce qui se passe en A : si cette valeur est strictement positive, alors A est un extremum local ; si elle est strictement négative, alors A est un point-selle. Si elle est nulle… tout est possible !

[/encadre]

L’idée générale sous-jacente aux propriétés de la seconde forme quadratique fondamentale revient à l’étude des directions des plans de coupe verticaux en A qui montrent les comportements les plus extrêmes des courbes obtenues : celle qui « va le plus vers le haut » et celle « qui va le plus vers le bas ». Dans le cas d’un minimum, par exemple, toutes les courbes obtenues par une coupe verticale se dirigent certes vers le haut, mais en général il y en a toujours deux qui se distinguent des autres, l’une pour être celle qui monte le plus vite et l’autre pour être celle qui monte le moins vite.

Ces directions extrêmes sont les directions principales de la surface en A. Ce sont elles que la seconde forme quadratique fondamentale permet de déterminer. Elle permet aussi de calculer les courbures principales, qui quantifient la convexité de ces deux courbes extrêmes (positive quand ça monte, négative quand ça descend).

Au-delà des surfaces

Le formalisme qui permet l’étude des extremums dans le cas de fonctions à deux variables est donc plus élaboré que celui des fonctions à une seule variable, mais ce formalisme garde tout de même bien des traces de ce qui se passe pour les courbes. Dans le cas encore plus général de fonctions à trois variables ou plus, le formalisme du cas de deux variables s’étend sans trop de mal, la principale difficulté étant qu’il devient impossible de représenter les choses à l’aide d’un dessin. L’abstraction s’impose alors comme définitivement supérieure à la simple intuition visuelle.