
Dans sa très belle autobiographie, le grand physicien du XXe siècle Richard Feynman raconte que, lorsqu’il était étudiant, il fit un jour la farce mathématique suivante. Quelqu’un avait posé la question de savoir si la forme d’un trace-courbe pouvait être décrite d’une manière mathématique. « Bien sûr ! répondit-il facétieusement. Ces courbes sont très spéciales. Elles sont faites de sorte que, à leur point le plus bas, quelle que soit la manière dont on la tourne, leur tangente est horizontale. » Et les autres étudiants de s’extasier devant cette propriété soi-disant unique…
Le mariage d’une courbe et d’une droite
Ce que Feynman savait, mais que curieusement les autres étudiants du Massachusetts Institute of Technology ignoraient, c’est que la tangente est horizontale au point le plus bas de n’importe quelle courbe un tant soit peu « lisse ». Une définition rudimentaire de la notion de tangente en un point d’une courbe suffit à s’en persuader. Donnons-nous une courbe C quelconque et « suffisamment régulière » (notion à définir précisément selon le contexte), ainsi qu’un point A sur cette courbe. La tangente à C en A est la droite qui épouse « le mieux » la forme de la courbe au voisinage du point A. Si l’on imagine que C est la forme d’une route suivie par une voiture, alors la direction de la tangente est celle que suivra cette voiture si, au point A, une grosse plaque de glace la fait subitement patiner et qu’elle ne peut plus contrôler sa direction.
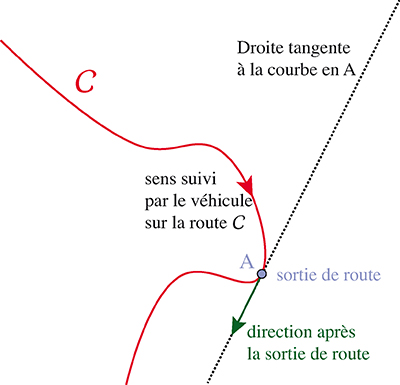
Pour visualiser la tangente, on peut aussi faire un zoom de plus en plus resserré autour de A. Si C est assez régulière, en zoomant « de plus en plus », on s’aperçoit qu’au voisinage immédiat de A, la courbe se confond pratiquement avec une ligne droite.
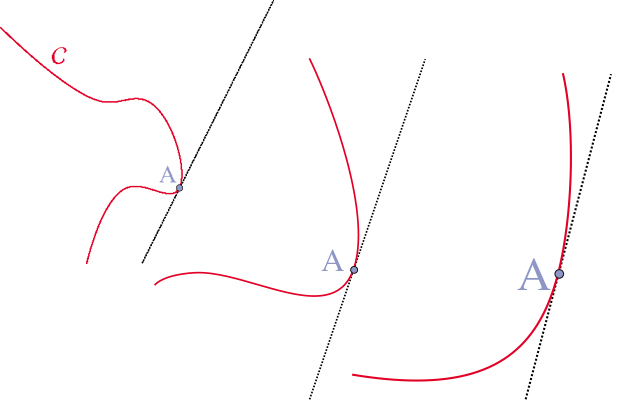
À mesure que l’on zoome sur le point A, le morceau de courbe autour de A
se confond de plus en plus avec la droite tangente en A.
Voyons maintenant ce qui se passe au point le plus bas d’une courbe. Se pourrait-il, comme le concevaient volontiers, semble-t-il, les petits camarades de Feynman, que la tangente n’y fût pas horizontale ? Supposons par exemple qu’elle descende vers la droite, comme le suggère le dessin ci-dessous.
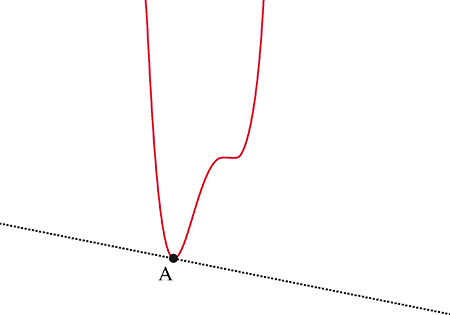
La géométrie étant l’art de raisonner juste avec des figures fausses, voyons quel problème pose ce dessin. Le point A est supposé être le plus bas de la courbe, mais la tangente est penchée. Un zoom autour du point A révèlera donc que, puisque la tangente « colle » à la courbe au voisinage de A, la courbe est en train de descendre lorsqu’on se déplace sur elle vers la droite en partant de A. Et donc, A n’est pas le point le plus bas de la courbe. La figure est donc contradictoire : si vraiment A est le point le plus bas, alors la tangente doit être horizontale (car, bien sûr, si l’on essaie d’envisager une tangente qui monte vers la droite au lieu de descendre, le raisonnement sera le même, en miroir).
Pentes dérivantes
Ce résultat mis en scène par Feynman est fondamental dans la recherche des valeurs optimales prises par une fonction. Une courbe C d’équation y = f(x) étant donnée, la pente de la tangente à C en un point (a, f (a)) est la valeur notée f ' (a) où f ' désigne la fonction dérivée de f. Tout point a pour lequel f prend la plus petite de ses valeurs vérifie donc l’équation f ' (a) = 0.
On dispose de beaucoup d’outils performants pour déterminer la dérivée d’une fonction f. En revanche, il peut se révéler très ardu de résoudre l’équation f ' (x) = 0, y compris lorsque la fonction f est relativement élémentaire. On en est alors réduit à faire des approximations, et c’est là un champ majeur de l’application des techniques numériques.
Enfin, il ne suffit pas non plus d’avoir trouvé un point où la dérivée s’annule pour pouvoir parler de minimum. Une fois trouvée une tangente horizontale, trois autres situations peuvent en effet se présenter.
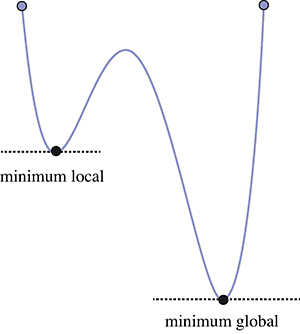
La première, c’est qu’il se peut que le minimum ne soit que local. La tangente ne nous renseigne que sur ce qui se passe au voisinage immédiat d’un point, et pas sur ce qui peut se passer ailleurs. Rien n’exclut donc, a priori, que le « vrai » minimum (que l’on qualifie de global) se trouve à un autre endroit.
Un deuxième cas est celui où, en un point où la tangente est horizontale, la fonction atteint en réalité un maximum (qu’il soit local ou global). Toute horizontale qu’elle soit, la tangente est en effet impuissante à elle seule à nous dire si l’on est à un plus haut ou à un plus bas. C’est là une conséquence de la perte d’information engendrée par l’approximation de la courbe par sa tangente : une droite peut approcher une courbe, mais ne peut nous dire si cette courbe est « au-dessus » (pour un minimum) ou « au-dessous » (pour un maximum).
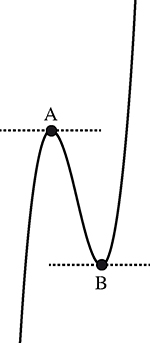
La tangente est horizontale pour un maximum comme pour un minimum.
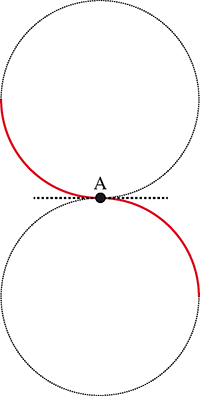
Les choses peuvent même être encore pires : la courbe peut se trouver des deux côtés de sa tangente. On parle alors de point d’inflexion. Un exemple est donné par la courbe constituée de deux quarts de cercles disposés comme dans la figure ci-dessous. Au point A, cette courbe admet bien une tangente au sens de notre définition, mais cette tangente la traverse : toute horizontale qu’elle est, elle ne correspond pas à un minimum de la courbe (ni à un maximum, d’ailleurs), fût-il local.
En nous donnant la pente de la tangente, la dérivation nous permet donc de dégrossir le travail dans la recherche des extremums, mais ne suffit pas à elle seule à finir le travail. D’autres outils doivent donc être mobilisés pour trancher entre les différents cas théoriquement possibles.
[encadre]
La question des bords
En toute rigueur, il n’est pas tout à fait vrai que la tangente à la courbe est toujours horizontale en son point le plus bas. En effet, lorsque ce point est atteint à l’une des extrémités de la courbe, la tangente n’est assujettie à aucune contrainte.
L’étude du comportement d’une fonction aux bords de son domaine de définition est un sujet en soi, qu’il peut être assez facile à traiter dans le cas de l’étude d’une courbe dans le plan mais qui devient vite plus élaboré dans le cas de fonctions de plusieurs variables.
[/encadre]
Lire la suite gratuitement