On a su définir l’enveloppe d’une famille de droites ; cet objet mathématique se prête à de jolies propriétés et figures géométriques. Pourquoi ne pas poursuivre dans cette voie et définir une notion d’enveloppe de familles de courbes (C _t) _t ?

Une première définition, naturelle, serait : « Courbe ou droite tangente à toutes les courbes C _t, pour chaque réel t. » Une seconde définition, plus rigoureuse, serait : « Lieu des points caractéristiques, à savoir les points communs à la courbe C _t et à une courbe “infiniment voisine” de la famille, c’est-à-dire à une courbe C _t’, où t’ est “infiniment voisin” de t. » Peut-on rendre ces deux points de vue compatibles ?

Le cas des droites

En fait, les deux définitions proposées sont… « presque » équivalentes. Voyons-le dans le cas d’une famille de droites (D_t) _t, d’équation générique a (t) x + b (t) y + c (t) = 0. Un réel « infiniment voisin » de t s’écrit t’ = t + dt, avec dt « petit ». La seule règle de calcul dont on a besoin est  f (t + dt) =  f (t) + f ’(t) dt lorsque f est une fonction dérivable.

La droite « infiniment voisine » de D _t a pour équation :

a (t + dt) x + b (t + dt) y + c (t + dt) = 0.

On obtient donc le point caractéristique en résolvant un système d’équations linéaires :

\( \left\{ \begin{array}{l l} a(t)x+b(t)y+c(t)=0,\\ a'(t)x+b'(t)y+c'(t)=0.\\ \end{array} \right. \)  

Si a (t) b’(t) – b (t) a’(t) n’est pas nul, ce qui signifie que la pente de la droite D_t n’est pas constante, ce système a, pour chaque t fixé, une solution unique x = X(t), y = Y(t). Ce sont les coordonnées du point caractéristique M(t). On en déduit que M(t) décrit une courbe quand t varie.

Pourquoi la courbe décrite par le point caractéristique est-elle tangente à la droite D_t ? Un petit calcul le montre immédiatement… même si l’on aimerait une explication plus géométrique. Puisque x = X(t) et y = Y(t) vérifient la première équation du système, on a en effet, pour tout t, a(t) X(t) + b (t) Y(t) + c(t) = 0.
En dérivant, on obtient : a’(t) X(t) + a (t) X’(t) + b’(t) Y(t) + b (t) Y’(t) + c’(t) = 0, d’où, en tenant compte du fait que x = X(t) et y = Y(t) vérifient la seconde équation du système,

a (t) X’(t) + b (t) Y’(t) = 0. Cela signifie que le vecteur vitesse du point (X(t), Y(t)) est parallèle à la droite D _t, ou encore, puisque M(t) appartient à D_t, que D_t est tangente à la trajectoire de (X(t), Y(t)).

Dans l’autre sens, partons d’une courbe paramétrique Γ, et notons D_t la tangente à Γ au point de paramètre t. Par construction, Γ est bien l’enveloppe des droites D_t au sens de la première définition ! 

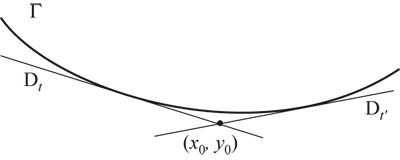
D’un des côtés de Γ (celui duquel on voit la courbe convexe), tous les points( x₀, y₀) appartiennent à deux droites différentes, D_t et D_t’, de la famille (D_t) _t. Lorsque ( x₀, y₀) se rapproche de Γ, les paramètres t et t’ se rapprochent, de même que les droites D_t et D_t’. Lorsque ( x₀, y₀) se confondent en un point de Γ, on peut considérer qu’il appartient doublement à la tangente en ce point (ou, selon une autre conception, qu’il appartient à deux courbes « infiniment voisines » de la famille).

Cette situation évoque celle d’une équation du second degré dont les coefficients varient : l’existence d’une racine double assure la transition entre la situation « deux racines distinctes » et la situation « pas de racine ».

L’usage des « droites doubles » et des « droites infiniment voisines » étant sujet à caution, on remplace la deuxième définition par une troisième… qui permet de passer au cas général d’une enveloppe de courbes. Supposons que la courbe C _t soit définie par une équation du type F (x, y, t) = 0. Fixons un point ( x₀, y₀). On détermine les courbes de la famille qui passent par ce point en résolvant l’équation en t F ( x₀, y₀, t ) = 0. Dans le cas de la figure précédente, cette équation possède deux racines distinctes. Si cette équation a une racine (au moins) double t (c’est-à-dire que l’on a  f (t) =  f ’(t) = 0), alors ( x₀, y₀) est par définition un point caractéristique de C _t. Le point ( x₀, y₀) est donc point caractéristique de C _t si F ( x₀, y₀, t ) = 0 et F’_t ( x₀, y₀, t ) = 0 (où, dans cette dérivée par rapport à t, x₀ et y₀ sont fixés). Comme dans le cas des droites, les points caractéristiques correspondent à des racines doubles et forment une courbe qui est tangente à chaque courbe C_t.

Il peut y avoir plusieurs points caractéristiques pour une même valeur de t. C’est le cas par exemple pour une enveloppe de cercles, puisque deux cercles « voisins » qui se rencontrent se coupent en deux points. 

Cette définition, où le mot « tangente » n’apparaît plus, a l’avantage de prendre en compte le cas où l’enveloppe d’une famille de droites est un point. Considérons ainsi la famille de droites y – tx = 0. Pour chaque valeur de t, le point ( x₀, y₀) = (0, 0) est caractéristique, et c’est le seul. Une quatrième définition, de nature bien plus géométrique, va nous éclairer…

Vers une définition moderne

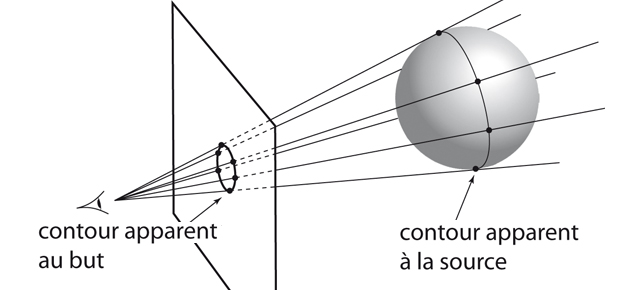
Le contour apparent d’un objet vu par un observateur, c’est ce que celui-ci dessine : l’intersection des rayons issus de l’œil, tangents à la surface de l’objet, avec le plan du dessin. Plaçons l’observateur à l’infini sur l’axe des z et le plan du dessin sur le plan ( x O y). Les rayons issus de l’œil de l’observateur sont dans ce cas les droites verticales. On peut aussi considérer le contour apparent d’une surface S qui ne limite pas un objet. La définition est la même ! Si la surface présente des plis ou des creux, il vaut mieux l’imaginer comme transparente.

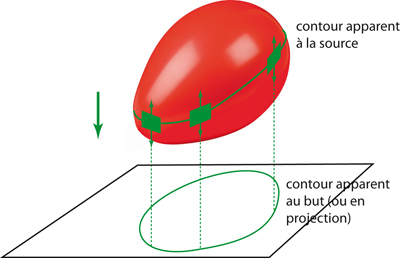
Le mathématicien français René Thom (1923–2002) suggérait de considérer deux courbes : d’abord l’ensemble des points de S où la verticale est tangente à S (cela définit une courbe tracée sur S, qu’il appelle contour apparent à la source), puis la projection de cette courbe sur le plan ( x O y), qu’il appelle contour apparent au but (ou en projection).

La définition de l’enveloppe d’une famille de courbes se glisse alors dans celle du contour apparent. Imaginons la courbe C_t dans le plan ( x O y) et élevons-la jusqu’à l’attitude z = t. En réunissant toutes les courbes obtenues, on obtient une surface S. L’ensemble des points de S où la verticale est tangente à S est l’enveloppe à la source, et sa projection sur ( x O y) est l’enveloppe au but.

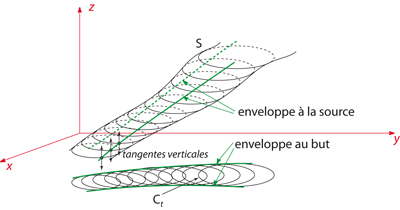
La définition de l’enveloppe au but coïncide avec les définitions précédentes de l’enveloppe. Géométriquement, dire que la verticale issue de ( x₀, y₀) est tangente à S, c’est dire que l’équation F ( x₀, y₀, t) = 0 a une racine double. 

Analytiquement, puisqu’un plan est vertical s’il contient une droite verticale, dire que
(x₀, y₀, t) est un point de S où la verticale est tangente à S, c’est dire que

F ( x₀, y₀, t ) = F’_t ( x₀, y₀, t ) = 0.

L’avantage de cette définition géométrique est que l’enveloppe à la source est toujours une « bonne courbe » (voir FOCUS), tandis que l’enveloppe au but peut présenter des singularités ou des défauts.