Entre 1620 et 1670, les plus prestigieux mathématiciens, comme René Descartes, Pierre de Fermat ou John Wallis, ont cherché à établir une méthode pour déterminer l’équation de la tangente à une courbe. L’introduction du calcul différentiel par Isaac Newton et Gottfried Wilhelm Leibniz à la fin du XVII ^e siècle a résolu ce problème de manière magistrale. On s’est aussitôt posé le problème inverse : étant donnée une famille de droites, peut-on trouver une courbe qui les admette toutes pour tangente ?

De la géométrie à l’analyse

x) et (Oy)

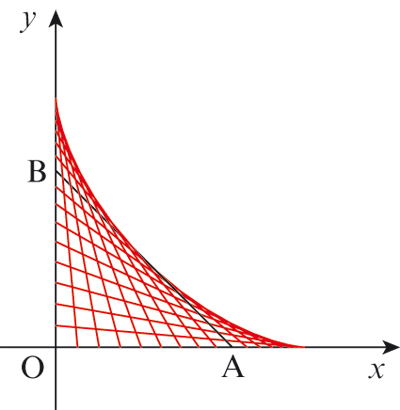
et faisons glisser un segment [AB] de longueur a tel que A soit sur l’axe (Ox) et B sur (Oy) :

on voit apparaître une courbe dont toutes les droites, obtenues en prolongeant ces segments, sont les tangentes.

Ces droites ont pour équation x cos t + y sin t = 5 sin 2 t. 

Après résolution (voir FOCUS), on obtient une astroïde, d’équation paramétrique t ↦ (cos³t, sin³t) ou d’équation cartésienne x ^2/3 + y ^2/3 = 1. On peut la visualiser en prenant une réglette d’une longueur donnée, en la plaçant un grand nombre de fois avec chacune de ses extrémités positionnées sur chacun de deux axes orthogonaux, et en traçant les droites correspondantes (voir article « Enveloppes, point courant et développées »).

Comme on le voit sur l’exemple précédent, il faut, pour voir apparaître une telle courbe, que la famille de droites possède une « certaine régularité » et que celles-ci se déduisent par un mouvement continu. En d’autres termes, il est nécessaire de définir analytiquement ces droites par ce que l’on appelle un paramétrage continu ; plus précisément, les droites doivent toutes vérifier une même équation qui dépend d’une variable t (appelée paramètre) et la fonction de t ainsi définie doit être continue, et même dérivable et de dérivée continue.

Pour mieux comprendre, prenons le problème à l’envers. Choisissons comme courbe le cercle unité du plan, défini par x ² + y ² = 1 (allons au plus simple !). La tangente au point courant (cos t, sin t) s’écrit D_t : x cos t + y sin t = 1. La méthode analytique se doit de faire le chemin inverse et, partant des équations des droites D_t , retrouver l’équation du cercle. Les exemples traitant souvent de problèmes cinématiques, la variable est souvent assimilée au temps mais, mathématiquement, ça n’a aucune importance.

Tschirnhaus, le précurseur

Le comte Ehrenfried Walther von Tschirnhaus (1651–1702).

La définition analytique précédente montre à l’évidence le besoin du calcul différentiel pour traiter ce type de problème. Aussi ne faut-il pas s’étonner que les premières recherches d’enveloppe de droites datent de la fin du XVII ^e siècle.

Le comte von Tschirnhaus (ou von Tschirnhausen) voit le jour dans le hameau de Kiesslingwalde (actuelle Sawnikowice en Pologne), à proximité de la petite ville allemande de Görlitz (actuel Land de Saxe). C’est pourtant à l’université de Leyde aux Pays-Bas, entre 1669 et 1674, qu’il va étudier les mathématiques, la physique, la philosophie et la médecine. Il s’initie à la pensée de Descartes. On l’introduit auprès de Baruch Spinoza, ce qui lui ouvre les portes des plus grands scientifiques et philosophes de l’époque.

Tschirnhaus voyage alors d’abord à Londres, où il rencontre Isaac Newton, Robert Boyle et John Wallis. Il se rend ensuite à Paris, où il fait la connaissance de Leibniz ; les deux hommes échangent sur le calcul différentiel que le savant allemand est en train d’élaborer. De nombreux courriers suivront cette rencontre.

Tschirnaus fait aussi connaissance de François Villette ; cet artificier avait mis au moins d’immenses miroirs permettant de réfléchir les rayons du soleil. Tschirnhaus se passionne alors pour l’optique et s’intéresse aux caustiques, visibles dans certaines expériences : c’est lui qui les appelle ainsi dès 1682 en utilisant le grec kaustikos (signifiant « qui brûle », en référence aux rayons lumineux qui engendrent de la chaleur). Il comprend l’intérêt du calcul différentiel pour les étudier. En 1682, il donne le premier calcul d’enveloppe en étudiant les rayons se réfléchissant sur une parabole ; il obtient une courbe, appelée de nos jours la cubique de Tschirnhaus.

Par la suite, Tschirnhaus mettra à profit ses compétences scientifiques pour inventer, avec Johann Friedrich Böttger, un procédé de fabrication de porcelaines dures qui sera à l’origine des porcelaines de Saxe.

Le mathématicien suisse Jean Bernoulli s’empare alors de ce sujet et publie un article en 1692 dans la revue Acta Editorum, dans lequel il donne l’équation de différentes caustiques, en particulier celle obtenue par la réflexion sur un miroir sphérique d’un faisceau de rayons lumineux parallèles entre eux.

Dans deux articles publiés en 1692 et 1694 dans la même revue, Leibniz donne une méthode générale pour trouver l’enveloppe d’une famille de courbes définies par un paramétrage continu. Si leurs équations s’écrivent  f (x, y, t) = 0, où t est le paramètre, il élimine t entre les deux équations  f (x, y, t) = 0 et ∂_t f (x, y, t) = 0 (le cas d’une droite est traité en encadré).

Le marquis Guillaume de l’Hospital, qui avait suivi les cours de Jean Bernoulli, propose alors une présentation de cette nouvelle théorie dans son ouvrage Analyse des infiniment petits pour l’intelligence des lignes courbes publié en 1696. Ainsi était établie en une quinzaine d’années une très belle théorie de géométrie, qui mettait en valeur l’utilisation du calcul différentiel juste naissant.