ébarbatif et inutile, le concept d’enveloppes de droites ? Voire ! Prenons un exemple concret, celui d’une porte d’autobus en deux morceaux qui se replie. Au sol, à l’arrêt (la porte est fermée), on obtient deux segments de droite. À l’ouverture de la porte, le segment à gauche va pivoter pour décrire un quart de disque. Le segment à droite est plus intéressant à étudier.

La projection sur le sol du battant droit de la porte est un segment. Durant le déplacement de la porte (voir le schéma qui suit), il définit une droite coupant deux droites perpendiculaires, (OA) matérialisant l’axe de la porte fermée et (OB) matérialisant l’axe de la porte ouverte, selon un segment [AB] de longueur constante (celle de la porte entière). Le triangle OAI est isocèle car les deux battants de la porte [OI] et [IA] (position à l’instant courant) ont même longueur. De même, OBI est isocèle car les deux battants de la porte [OB] et [IO] (position à l’arrivée) ont même longueur. Ainsi, [AB] a une longueur constante (voir FOCUS).

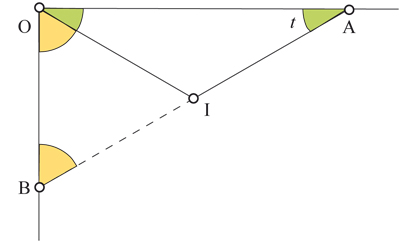
Il est facile de tracer un grand nombre de segments [AB]. On voit alors apparaître une courbe en négatif. Cette enveloppe a deux propriétés distinctes. En premier lieu, elle délimite la surface que parcourt la porte, celle où l’on peut se placer sans se faire bousculer. D’un autre, les droites (AB) sont toutes tangentes à l’enveloppe. Cette propriété se prête mieux au calcul que l’autre.

Le point courant de Monge

Pour étudier cette enveloppe, on commence par écrire l’équation de (AB) en fonction de l’angle t en A. Si la longueur AB est égale à a, il est relativement facile de déterminer l’équation de la droite ; on trouve D(t) : x sin t + y cos t = a (cos t)(sin t). L’enveloppe est tangente à D(t) en un point dit caractéristique, intersection de D(t) et de sa dérivée D’(t). Les coordonnées de ce point M(t) sont donc solutions du système 

\( \left\{ \begin{array}{l l} x \sin t + y \cos t = a (\cos t) (\sin t),\\ x \cos t - y \sin t = a \cos^2 t -a \sin^2 t.\\ \end{array} \right. \)

On en déduit les coordonnées du point caractéristique de D(t) : 

\( \text{M}(t) \left | \begin{array}{l l} x = a \cos^3 t,\\ y = a\sin^3t.\\ \end{array} \right. \)

Ce point décrit une courbe nommée astroïde.

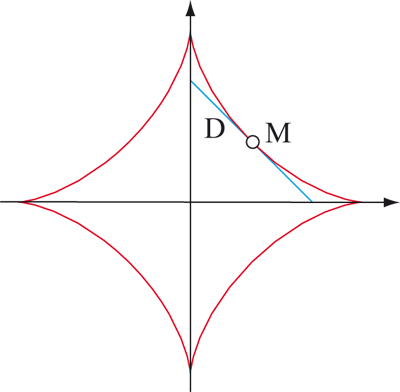
L’astroïde (en rouge) est l’enveloppe des droites D (en bleu) avec le point caractéristique M de D.

Construction de l’astroïde.

Le point caractéristique de D est le point courant de l’enveloppe. Il se définit de façon générale comme un point limite, celui de l’intersection de D = D(t) et D(t + ε) quand ε tend vers zéro. Il s’agit du point d’intersection de D et D’ si les équations de D(t) s’écrivent
u(t) x + v (t) y + w (t) = 0 où u, v et w sont des fonctions continûment dérivables sur un intervalle I telles que u v’ – u’ v ne s’annule pas. Ainsi, déterminer l’enveloppe d’une famille de droites D(t) revient à calculer le point courant de Monge, ou point caractéristique de D(t).

Si vous êtes curieux, vous aurez sans doute remarqué une courbe étrange dans votre bol du petit déjeuner. On peut la retrouver en posant une bague sur sa main ou au sol. Faites l’expérience et vous ne pourrez plus l’oublier ! On s’en aperçoit vite : ce phénomène est créé par la réflexion des rayons lumineux sur un cercle, mais quelle est cette courbe ? Peut-on déterminer son équation et ses propriétés ?

Il est facile d’étudier la famille des rayons lumineux réfléchis sur un cercle. On trace les rayons venant du soleil, puis les rayons réfléchis sur le cercle. Le lien entre les deux est simple : ils font des angles égaux avec la normale au cercle au point d’incidence. Si l’on choisit comme axe des x la droite orientée vers le soleil, on obtient le dessin ci-dessous.

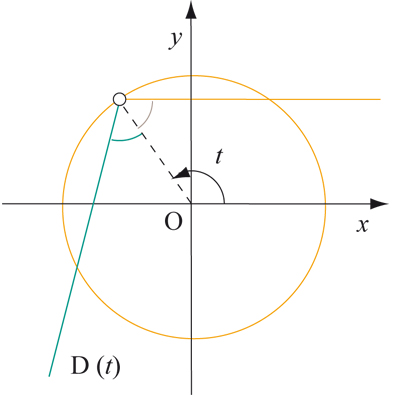
Les rayons venant du soleil (en orange) sont réfléchis (en vert) sur le cercle.

L’ensemble des rayons réfléchis sur le cercle de centre O et de rayon R peut être paramétré en fonction de l’angle polaire t du point d’incidence sur le cercle. On aboutit à une droite D(t) d’équation x sin 2t – y cos 2t – R sin t = 0. En traçant cette famille de droites, on obtient la figure ci-dessous.

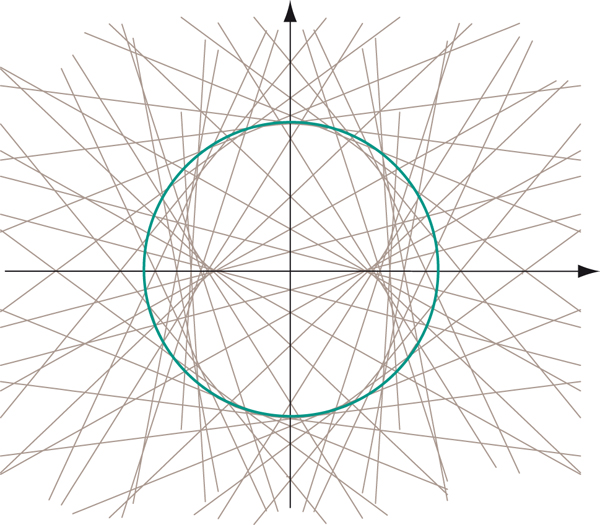
Tracé de la famille des rayons réfléchis.

Les rayons réfléchis se focalisent sur les points de Monge, donc sur leur enveloppe ! On détermine le point caractéristique de D(t) comme solution du système {x sin 2t – y cos 2t – R sin t = 0 et 2 x cos 2t + 2 y sin 2t – R cos t = 0}. On obtient le paramétrage suivant de la courbe cherchée :

  \( \left\{ \begin{array}{l l} x (t) = \text{R} \left( \sin t \sin 2t + \dfrac {(\cos t) (\cos 2t)}{2} \right) ,\\[3mm] y (t) = \text{R} \left( - \sin t \cos 2t + \dfrac {(\cos t) (\sin 2t)}{2} \right) .\\ \end{array} \right. \)  

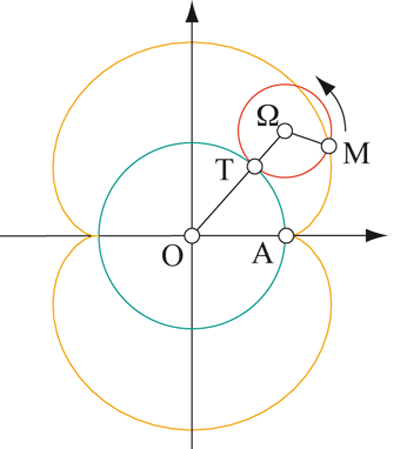
Quand le cercle de centre Ω roule sans glisser sur le cercle de centre O et de rayon double, il décrit une néphroïde. Les calculs se font en remarquant que l’angle \( \widehat{\text{T} \Omega \text{M}}\)  est le double de l’angle \( \widehat{\text{OAT}}.\)

La courbe trouvée a été baptisée néphroïde à cause de sa ressemblance à un rein (on retrouve la racine grecque néphros dans l’expression « colique néphrétique »). En utilisant les formules de trigonométrie, on peut simplifier son paramétrage en :

\( \left\{ \begin{array}{l l} x (t) = \dfrac{ \text{R}}{4} (3 \cos t - \cos 3t) ,\\[3mm] y (t) = \dfrac{ \text{R}}{4} (3 \sin t - \sin 3t) .\\ \end{array} \right.\)  

Ces équations sont celles d’une épicycloïde, c’est-à-dire le lieu du point d’un cercle roulant sans glisser sur un autre. Dans le cas de la néphroïde, le cercle roulant a un rayon moitié de celui du cercle fixe.

Développée d’une courbe

La développée d’une courbe est, par définition, l’enveloppe de ses normales. Si la courbe est une source lumineuse, la développée est donc le lieu où se concentrent les rayons lumineux émis. On doit pouvoir ainsi visualiser la développée d’une courbe avec des tuyaux LED ; avis aux bricoleurs ! Pour notre part, voyons comment déterminer la développée d’une courbe sur l’exemple de la néphroïde précédente. Tout d’abord, il s’agit d’écrire la normale N(t) à la néphroïde en son point de paramètre t. Après des simplifications utilisant les formules usuelles de trigonométrie, on trouve l’équation 

  \( x \cos 2t + y \sin 2t = \dfrac{\text{R}}{2} \cos t.\)

L’équation de N’(t) s’obtient en dérivant. Le point de Monge P(t) est donc solution du système  

\( \left\{ \begin{array}{l l} x \cos 2t + y \sin 2t = \dfrac{ \text{R}}{2} \cos t ,\\[3mm] x \sin 2t + y \cos 2t = \dfrac{ \text{R}}{4} \sin t .\\ \end{array} \right. \)  

On en déduit les coordonnées de P(t) :

  \( \left\{ \begin{array}{l l} x (t) = \dfrac{ \text{R}}{4} \left(2 (\cos t) (\cos 2t) + (\sin t) (\sin 2t)\right) ,\\[3mm] y (t) = \dfrac{ \text{R}}{4} \left(2 (\cos t) (\sin 2t) - (\sin t) (\cos 2t)\right) .\\ \end{array} \right. \)  

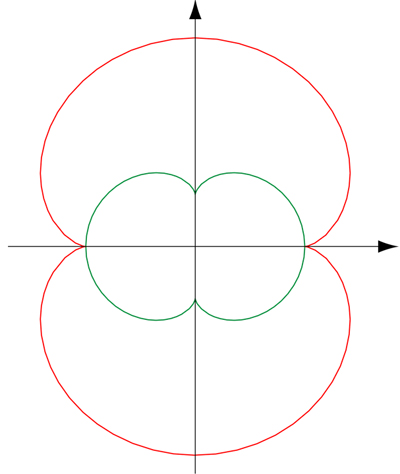
La néphroïde (en rouge) et sa développée (en vert).

Sur le schéma, la développée semble se déduire de la néphroïde par la similitude de centre O, d’angle 90° et de rapport 1/2. C’est effectivement bien le cas et ce résultat se généralise à toutes les courbes cycloïdales !