Si l’on prend soin d’effacer une courbe plane après avoir tracé plusieurs de ses tangentes, l’œil devine malgré tout la forme de la courbe originelle, comme enveloppe de l’ensemble de ces droites. Notre cerveau a en fait résolu, approximativement, un problème de géométrie différentielle qui consiste à déterminer, dans le cas général, la courbe, dite enveloppe, tangente à une famille de courbes à un paramètre λ d’équation  f (x, y, λ) = 0. Analytiquement, il s’agit de résoudre le système :
\( \left\{ \begin{array}{l l} f (x, y, \lambda ) = 0,\\[3mm] \dfrac{\partial f}{\partial \lambda} (x, y, \lambda ) = 0, \\ \end{array} \right. \)

dans lequel la seconde équation caractérise le point de tangence. Dans le cas d’une famille de droites, le point courant de l’enveloppe apparaît alors comme l’intersection de deux droites. Pour les coniques, abondamment étudiées depuis Apollonius, la construction d’une tangente est simple, ce qui en permet une réalisation par pliage.

Coniques encerclées

Les coniques, courbes planes définies analytiquement par une équation du second degré, sont géométriquement les coupes d’une surface de révolution engendrée par une droite. Si cette droite passe par l’axe de révolution, on obtient un cône dont les coupes, suivant l’orientation du plan, produisent une ellipse, une parabole ou une hyperbole. Si la droite est hors axe et parallèle à l’axe de rotation, on a un cylindre, qui ne peut fournir que des ellipses (dont les cercles). Sinon, on a un hyperboloïde de révolution à une nappe, en forme de diabolo. Dans les cas dégénérés, on obtient une droite, deux droites ou un point (voir Tangente SUP 75, 2014).

En général, une conique possède deux foyers. Pour le cercle, ils sont confondus, et pour la parabole, l’un d’entre eux s’égare à l’infini. On note 2c la distance des foyers et 2a la distance des points de la conique sur l’axe des foyers. Le paramètre caractéristique des coniques est l’excentricité e = c / a. Pour une ellipse, 0 < e < 1. Pour une hyperbole, e > 1. Pour un cercle, e = 0 et, pour l’improbable parabole, e = 1. Voyons maintenant une construction générale des coniques qui permet de définir la tangente en tout point.

Soient un cercle (C_p ), dit principal, et deux points F₁ et F₂, les foyers, symétriques par rapport au centre de ce cercle. Si les foyers sont intérieurs au cercle principal, on construit une ellipse, sinon, une hyperbole.

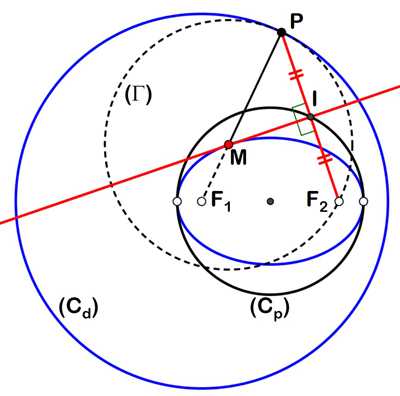
Tangente à une  ellipse.

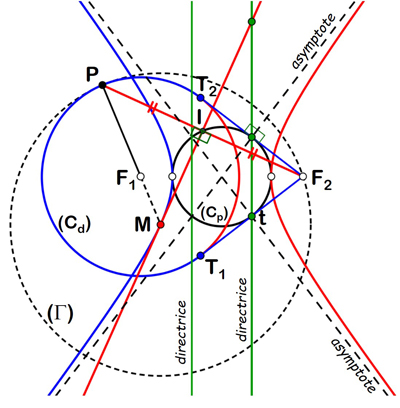
Tangente à une  hyperbole.

On considère l’homothétie de centre le foyer F₂ et de rapport 2. Cette transformation fait correspondre au cercle principal (C_p ) en noir le cercle directeur (C_d ) en bleu. Le cercle (C_p ) est intrinsèque à la conique, tandis que (C_d ) est lié à sa construction.

Alors, pour tout point courant P de (C_d ), la médiatrice du segment [PF₂ ] est une tangente à la conique cherchée en M, point situé à l’intersection de cette médiatrice et du segment [PF₁ ]. L’intersection de cette tangente avec le segment [PF₂ ], par construction le milieu I du segment [PF₂ ], se situe sur le cercle principal. Au cours du déplacement du point P, le cercle ( Г ) de centre M passant par P est toujours tangent au cercle directeur en P et passe par le foyer F₂.

Familles de médiatrices

Pour une hyperbole, les deux cercles, principal et directeur, s’interceptent. Les tangentes au cercle principal issues d’un foyer définissent les directrices de l’hyperbole. Les perpendiculaires à ces tangentes aux points de tangence sont les asymptotes, marquant la frontière entre les deux branches de l’hyperbole. À l’arc vert  du cercle directeur correspondent les tangentes vertes, à l’autre partie de la circonférence en rouge les tangentes rouge.

Pour la parabole, il suffit de considérer le second foyer à l’infini pour obtenir une construction en tout point similaire à celles de l’ellipse et de l’hyperbole. Le cercle directeur (C_d) change de genre en devenant directrice et (C_p) se confond avec la tangente à l’origine, mais (C_d) est toujours l’image de (C_p) dans l’homothétie de centre F₂ et de rapport 2.

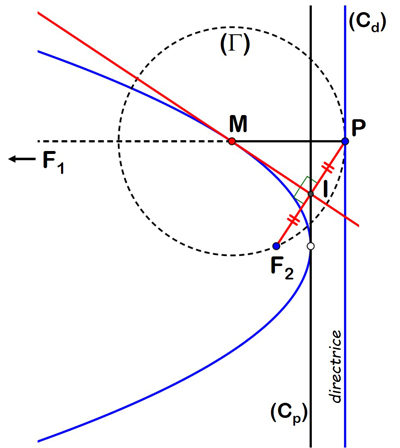
Tangente d’une parabole.

Ainsi, les coniques sont les enveloppes d’une famille de médiatrices. On aurait également pu construire ces tangentes comme les perpendiculaires au point courant I du cercle principal au segment [ IF₂ ], mais au prix d’une perte de simplicité et de généralité.

Plicatures et effections

L’élément constitutif de l’art de l’origami japonais étant une singularité droite, le pli (voir Tangente 146), on peut donc, en suivant les méthodes géométriques décrites, faire apparaître la silhouette d’une conique par plicature.

Un cercle étant tracé, il suffit d’effectuer les plis qui font coïncider un point quelconque de ce cercle à un point donné du plan, un foyer de la conique, l’autre foyer étant le centre du cercle. Si le point choisi est interne au cercle, on obtiendra une ellipse, sinon ce sera une hyperbole (voir les figures suivantes).

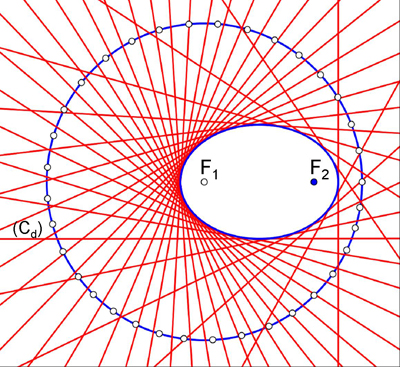
Enveloppe elliptique.

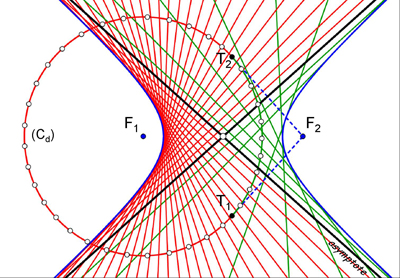
Enveloppe hyperbolique.

Cette méthode devient plus simple pour la parabole, car les cercles deviennent des droites ! En prenant le bord de la feuille pour directrice, il n’y a qu’un point à dessiner, le foyer, pour obtenir par le même type de plicature l’enveloppe d’une parabole.

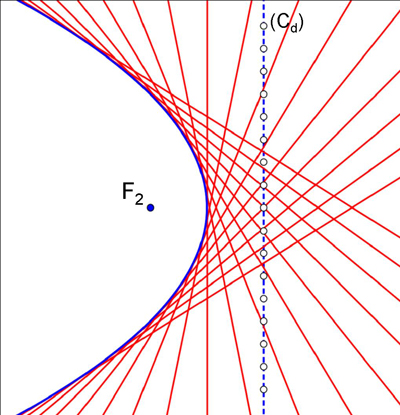
Enveloppe parabolique.

Les pliages d’origamis permettent aussi d’établir des constructions géométriques impossibles au compas seul. En effet, si les cinq premiers axiomes de l’origami ont la même puissance constructive que le compas, l’ajout du sixième permet de résoudre, par effection (c’est-à-dire de manière géométrique explicite et constructive), des équations du troisième degré. Ainsi, des problèmes historiques tels que la duplication du cube ou la trisection de l’angle deviennent possibles.

Les axiomes de l’origami

Initiée depuis Euclide, la recherche des nombres et polygones du plan usuel constructibles, en un nombre fini d’étapes, à la règle (non graduée) et au compas a abouti aux théorèmes de Wantzel sur les nombres constructibles et au théorème de Gauss–Wantzel pour les polygones constructibles. On sait depuis le Danois Georg Mohr, en 1672, qu’une construction dite à la règle et au compas peut être en fait effectuée au compas seul (voir la Droite, Bibliothèque Tangente 59, 2017 ; le Cercle, Bibliothèque Tangente 36, 2009 ; et les Angles, Bibliothèque Tangente 53, 2015).

Passons maintenant en revue ces fameux axiomes de l’origami, qui se rapportent eux aussi au plan usuel et qui sont si différents de ceux d’Euclide.

En fait, la mathématisation de l’art ancestral de l’origami n’a eu lieu que récemment. Dans les dernières années du XX ^e siècle, Jacques Justin d’abord, puis Humiaki Huzita (1924–2005) et Koshiro Hatori, ont établi les sept axiomes suivants :

A1 : un unique pli passe par deux points donnés (géodésique).

A2 : un unique pli superpose deux points donnés (médiatrice).

A3 : deux droites données sont superposables par un pli (bissectrices).

A4 : un unique pli passe par un point donné et est perpendiculaire à une droite donnée (perpendiculaire).

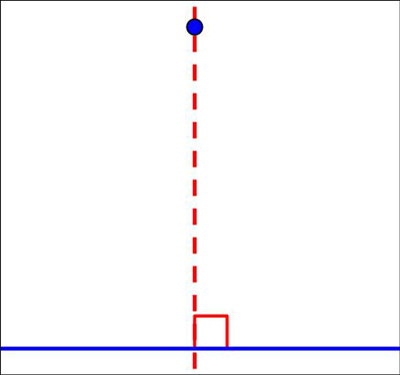
A5 : pour une droite D et deux points A et B donnés, un pli adéquat, quand il existe, passe par A et amène B sur D (intersection d’une droite et d’un cercle).

Cas de deux solutions.

A6 : ppour deux droites D₁ et D₂ et deux points A et B donnés, un pli adéquat, quand il existe, amène A sur D₁ et B sur D₂ (tangente commune à deux paraboles).

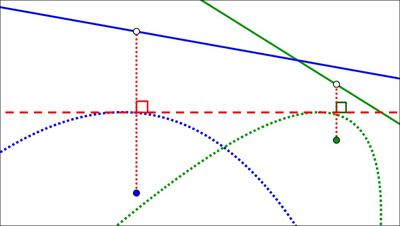
Pli de Beloch tangent à deux paraboles.

A7 : pour un point A et deux droites D₁ et D₂, un pli adéquat amène A sur D₁ tout en étant perpendiculaire à D₂.

L’Américain Robert Lang a prouvé que cette liste d’axiomes est complète pour la construction géométrique par l’origami à un seul pli. Par contre, si l’on autorise deux plis simultanés, l’axiome 4 n’en est plus un car il se déduit alors des axiomes 1 et 2. On peut également discuter de l’utilité du septième axiome qui, lui aussi, se déduit des axiomes 1 et 2 dans le cas de deux plis simultanés et qui semble, de plus, ne rien devoir apporter par rapport aux six autres…

Pour tout géomètre, un point, le foyer, et une droite, la directrice, caractérisent une parabole. D’après la construction des paraboles qui a été décrite, le pli qui amène le foyer sur la directrice est la tangente à cette parabole. Trouver le pli qui répond à l’axiome 6 revient donc à déterminer une tangente commune à deux paraboles, c’est-à-dire à résoudre une équation du troisième degré. C’est le pli de Beloch, du nom de la mathématicienne italienne Margherita Piazzola Beloch (1879–1976), connue pour ses travaux en géométrie algébrique et topologie, qui montra en 1936 qu’une équation quelconque de troisième degré peut effectivement être résolue par origami. Un résultat spectaculaire !

Et la recherche origamique continue. Il a ainsi été montré qu’en autorisant n plis simultanés, il est possible de résoudre toute équation polynomiale de degré n + 2. Mais la puissance constructive des plis multiples n’est pas encore maîtrisée, loin de là…