Ci-dessus : Une cuillère enfermée dans une ampoule scellée pour un test de psychokinèse.

Les personnes qui possèdent des capacités « extrasensorielles » (ou plutôt qui sont censées posséder de telles aptitudes) seraient le premier enfant d’un couple. Le pouvoir reviendrait au fils aîné. C’est lui, et peut-être lui seul, qui pourrait récupérer les dons de guérisseur de la mère ou hériter du don de magnétiseur du père… En d’autres termes, pour la réception d’un tel don, c’est la prévalence de la primogéniture qui semble s’appliquer.

Prenons l’exemple du troublant droit d’aînesse chez les médiums (voir par ailleurs l’ouvrage référencé en fin d’article). Par sujet-psi, on désigne une personne capable d’appréhender un phénomène supposé mettant en jeu le psychisme et son interaction avec l’environnement. Imaginons que de longues enquêtes menées sur le terrain aient abouti à la constatation suivante : la plupart des grands sujets-psi et médiums sont des fils (ou filles) aînés. Eh bien, aussi curieux que cela puisse paraître, enquêtes et statistiques (qui peuvent être vérifiées) le montrent : le résultat demeure indubitablement que la majorité des grands sujets-psi ou médiums sont effectivement des fils aînés, donc n’ayant pas (et n’ayant jamais eu) de frères ou sœurs plus âgés qu’eux.

C’est la première étape de la démarche : s’assurer de la matérialité des faits, comme nous le rappelle Bernard Le Bouyer de Fontenelle en 1687 dans son ouvrage Histoire des oracles : « Assurons-nous bien du fait, avant de nous inquiéter de la cause. Il est vrai que cette méthode est bien lente pour la plupart des gens, qui courent naturellement à la cause, et passent par-dessus la vérité du fait ; mais enfin nous éviterons le ridicule d’avoir trouvé la cause de ce qui n’est point. »

Des médiums et des vampires

Les faits étant assurés et la forte corrélation entre les deux variables (« être l’aîné » et « avoir des dons ») étant ainsi constatée, les théoriciens de la parapsychologie tenteraient sans doute de bâtir un lien causal comme explication. « Parapsychologie » ? Une définition pourrait être : « Pseudoscience qui désire étudier des aptitudes humaines dites spéciales que, pour l’instant, personne n’a jamais observées dans le cadre d’une démarche méthodologique scientifique correcte. »

L’hypothèse la plus vraisemblable s’avère alors être la suivante : l’influx médiumnique transmissible, des dons divins de devin, provenant probablement pour petite partie des parents, des grands-parents, ou d’autres ascendants, s’épuise peut-être presque entièrement lors de la transmission au premier-né et n’est donc quasiment plus disponible pour les enfants suivants.

Si l’on s’intéresse à d’autres domaines que le mesmérisme ou la médiumnité, on s’apercevra alors, preuves statistiques à l’appui, que, par exemple, la plupart des grands chasseurs de vampires sont des fils aînés. Et, signe manifeste d’un incroyable complot, nous pourrons, toujours chiffres à l’appui, constater que la plupart des grands peintres qui adorent les teintes rouge sang sont aussi des fils aînés !

Les hypothèses implicites

On pourrait d’ailleurs faire la prédiction que la plupart des lecteurs de cet article sont des fils aînés, et de même que la plupart des lectrices de cet article sont des filles aînées. En fait, ce qui est incroyable et pourtant vrai, c’est que la plupart des grands [ce que vous voulez] sont des fils aînés ! Il s’agit d’une fausse corrélation. Le point central de toutes ces déclarations repose sur une hypothèse implicite : les fils ou filles aînés sont moins nombreux que les autres. Mais, les familles étant la plupart du temps de taille réduite, cette évidente hypothèse est en réalité fausse. Voyons pourquoi en nous penchant sur le cas des garçons (le raisonnement est identique dans le cas des filles). On suppose ici l’équiprobabilité de naissance pour un garçon G et pour une fille F, ce qui n’est pas la stricte réalité mais n’intervient en rien dans le raisonnement. L’ordre des lettres correspond à l’ordre de naissance (ainsi, FGF correspond à la naissance d’une fille, puis d’un garçon, puis encore d’une fille). Examinons les différents cas de famille qui peuvent se présenter.

• Famille avec un enfant : les possibilités sont F ou G. Soit, pour ce qui concerne les seuls garçons, un fils aîné sur un garçon, donc 100 % d’aînés.

• Famille avec deux enfants : les possibilités sont FG, GF, FF ou GG, soit trois fils aînés sur quatre garçons, c’est-à-dire 75 % d’aînés.

• Famille avec trois enfants : les possibilités sont FFF, FFG, FGF, GFF, FGG, GFG, GGF ou GGG, soit sept fils aînés sur douze garçons, c’est-à-dire environ 58 %.

• Famille avec quatre enfants : on dénombre (faites-le !) quinze fils aînés sur trente-deux garçons, c’est-à-dire environ 47 %. À partir de cette taille de famille, les aînés deviennent donc minoritaires.

• Famille avec cinq enfants : dans tous les cas sauf 1 (celui où ne naissent que des filles), il y a forcément un garçon aîné. Donc on compte au total trente et un garçons aînés. Le nombre total de garçons étant la moitié du nombre total d’enfants (cinq enfants dans chacun des trente-deux cas, soit un total de cent soixante enfants), on a donc environ 39 % d’aînés.

Ainsi, contrairement à ce que l’on pouvait supposer a priori, les fils aînés sont plus nombreux que les autres lorsque les familles sont, en moyenne, de taille réduite, comme cela est le cas en France (où les familles de quatre enfants ou plus représentent moins de 5 % du nombre total de familles avec enfants). Autrement dit, dans de telles contrées, la plupart des fils sont des fils aînés. Toute affirmation du type « La plupart des grands [ce que vous voulez] sont des fils aînés » ne présente pas vraiment un intérêt fondamental pour la recherche de quelque phénomène que ce soit…

Les mensonges, les sacrés mensonges et les statistiques

Les résultats statistiques sont souvent présentés comme la preuve d’un phénomène mais il s’en faut parfois de beaucoup pour que cela corresponde à la réalité des choses. Il faudrait par exemple déjà connaître les conditions exactes dans lesquelles les données ont été recueillies, connaître également le nombre de recherches et d’expériences qui ont été faites… Pour un phénomène qui n’existerait pas (ce qui est le cas par exemple de la voyance), il suffit d’effectuer un très grand nombre de recherches et d’expériences pour que l’une d’entre elles (ou même quelques-unes d’entre elles) produise un résultat positif en faveur de l’existence du phénomène en question. Et si l’on « oublie », comme cela est souvent le cas, de situer cette expérience dans le « flot » global, ce résultat pourra même être… statistiquement significatif.

C’est cela qui importe. Ceci est à relier à l’interprétation à donner aux résultats une fois ceux-ci scientifiquement acquis. Est-ce qu’une chose pourrait être vraie partout (dans tous les endroits, pour tous les sous-groupes…) mais fausse globalement ? Ou, à l’inverse, fausse partout mais vraie globalement ? La réponse est oui !

Prenons l’exemple d’un laboratoire qui déciderait de faire des expériences sur la perception extra-sensorielle et de tester Monsieur Psi, une personne prétendant ou pensant sincèrement disposer de dons de médium. 

Pour cela, il faut avoir un « sujet témoin », un « étalon de comparaison », et ce sera donc un individu « normal », ne revendiquant aucun pouvoir paranormal (ce qui ne veut pas dire qu’il n’en a pas !), à savoir Monsieur Lambda. L’expérience consiste à tester le don de Psi de prédire une carte tirée au hasard. Pour ce faire, chacun des deux sujets est placé devant une machine électronique effectuant un tirage aléatoire de cartes. M. Psi se concentre et tente de prédire la carte tirée. M. Lambda, lui, se contente de dire ce qui lui vient à l’esprit. Les deux sujets sont autorisés à passer quand ils le veulent, c’est-à-dire à ne rien annoncer, l’essai ne comptant donc pas dans le total (M. Psi peut être fatigué par sa concentration extrasensorielle intense et M. Lambda peut rêvasser et oublier de temps en temps l’expérience).

Une première longue série de nombreux tests donne les résultats suivants :

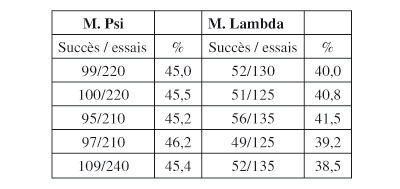
Comme on peut le constater, M. Psi a chaque fois été meilleur que M. Lambda dans ses annonces et, au total, il a prédit correctement cinq cents cartes sur un ensemble de mille cent essais, soit un taux de réussite de 45,5 %. M. Lambda a, quant à lui, nommé par hasard deux cent soixante cartes justes sur un total de six cent cinquante tentatives, soit 40,0 %.

On ne chante pas encore les louanges de M. Psi mais tout de même il a obtenu systématiquement un taux de réussite supérieur à celui de M. Lambda. On organise donc une deuxième longue série de tests, dont voici les résultats globaux.

M. Psi réussit six cents prédictions exactes sur un total de neuf cents, soit un taux de réussite de 66,7 %.

M. Lambda a, de son côté, nommé correctement huit cent quatre-vingts cartes sur mille trois cent cinquante, soit 65,2 %.

Confirmée donc par cette deuxième série, l’hypothèse d’un véritable pouvoir extra-sensoriel chez M. Psi prend de l’ampleur et différentes chaînes de télévision ne vont pas tarder à vanter urbi et orbi la découverte. Mais, horreur, un vilain zététicien fait remarquer que si, au lieu de considérer les deux séries indépendamment, on les regroupe pour faire un seul bloc (ce qui est, ici dans le cadre des expériences en question, parfaitement légitime), les résultats sont les suivants. M. Psi a prédit correctement 500 + 600 soit mille cent cartes sur un total de deux mille tirages, soit un taux de réussite de 55,0 % ; alors que M. Lambda, en toute simplicité et sans aucun pouvoir allégué, a nommé correctement 260 + 880 soit mille cent quarante cartes sur le même total de deux mille tirages, soit un taux de 57,0 %. Ainsi, M. Lambda semble avoir plus de fluide extra-sensoriel que M. Psi ! Ou alors, M. Psi n’en a pas du tout…

Le paradoxe de Yule–Simpson

Le joli paradoxe précédent, dit paradoxe de Yule-Simpson (voir les Probabilités au cœur de la modernité, Tangente SUP 73–74, 2014), possède une valeur formatrice. Il montre combien il est difficile de concevoir des expériences dont l’analyse statistique des résultats soit vraiment indiscutable ! C’est surtout vrai dans des recherches en sciences sociales, en statistiques médicales, en génétique des populations, ou encore en économie. De plus, il montre la nécessité d’avoir à sa disposition des tests permettant de pouvoir évaluer concrètement la significativité à accorder à la divergence d’un résultat par rapport à un autre (problème dit du choix de H₀ ).

Enfin, il est bon de se rappeler que le droit au rêve a pour pendant le devoir de vigilance…