Si le concept de nombre, historiquement parlant, a d’abord été attaché au nombre entier, il s’est étendu ensuite à bien d’autres catégories, des rationnels aux réels, puis aux complexes. À chaque stade de ces « inventions », un pas décisif pour les mathématiques et leurs applications a été franchi. Une vaste épopée, qui se poursuit encore aujourd’hui ! Limitons-nous ici aux premières apparitions du nombre et à leur diffusion dans le pourtour du bassin méditerranéen : Mésopotamie, Égypte, Grèce et Rome.

Premières tentatives

« Les nombres, disait le mathématicien allemand Richard Dedekind dans son ouvrage de 1893 Was sind und was sollen die Zahlen ?, sont des créations libres de l’esprit humain. Ils servent de moyen pour appréhender plus facilement et avec plus d’acuité la diversité des choses. » C’est justement pour traduire la réalité du monde que les peuples primitifs ont exercé, même sous des formes rudimentaires, une activité numérique. Au Paléolithique (il y a environ trente mille ans), on trouve déjà les toutes premières collections d’objets qu’on a pu qualifier de « bâtonnets de comptage », ou les premières marques sur des supports de bois ou d’os, pouvant représenter des quantités. On retrouve la matérialisation d’objets à compter non plus par des bâtons, mais par des « bulles ». Dans ces espèces de boules creuses en argile, on pouvait inclure des jetons, en argile également, qui symbolisaient les quantités à évaluer. Pour vérification, il fallait briser les bulles, si bien qu’on commença, vers la fin du IV^e millénaire avant notre ère, à y inscrire des symboles. Alors, pourquoi ne pas écraser les bulles pour en faire des tablettes où graver les mêmes informations ? L’idée d’écrire les nombres était née.

Dire et écrire les nombres

Les documents les plus anciens attestant de l’existence de véritables systèmes numériques, issus des vallées du Nil, du Tigre et de l’Euphrate, sont des hiéroglyphes représentant les nombres, allant jusqu’à 1 000 000 même, trouvés dans la tombe du roi Narmer (première dynastie égyptienne) datant d’environ 3 000 avant notre ère : des bâtons pour les unités, une anse de panier pour 10, un ruban enroulé pour 100, une fleur de lotus pour 1 000, un doigt levé pour 10 000, un oiseau stylisé pour 100 000, un dieu pour 1 000 000. La numération de l’Égypte antique était une numération de juxtaposition, donnant priorité au nombre 10 et à ses multiples, où l’addition et la soustraction se font sans difficulté.

Hiéroglyphes égyptiens représentant des nombres.

Les Grecs de l’Antiquité ont eu, eux aussi, une numération de juxtaposition, qui, sous diverses formes, avec des systèmes assez différents, a eu cours à partir du V^e siècle avant notre ère. Sans qu’on soit sûrs que des systèmes de numération plus « primitifs » aient existé avant l’introduction de l’alphabet, que les Grecs ont adopté du phénicien, attardons-nous sur les principaux d’entre eux, tous deux liés à l’existence d’un alphabet : la numération dite acrophonique et la numération alphabétique. Les deux utilisent la base 10, comme la plupart de leurs voisins méditerranéens, donnant au nombre 10 et à ses puissances des places privilégiées.

La numération acrophonique, désignée ainsi parce que ses signes ne sont rien d’autre que les initiales des noms des nombres, utilisait peu de symboles :

Les symboles élémentaires sont | pour 1, Γ  (gamma) pour 5 (penta, comme dans « pentagone »), Δ pour 10 (deka, comme dans « décamètre »), H pour 100 (hekaton, comme dans « hectomètre »), X pour 10 000 (kiliol, comme dans « kilomètre »), M pour 10 000 (myrioi, comme dans « myriade »).

Les symboles composés, avec des petites lettres à l’intérieur des grandes, associent le Γ du 5 aux puissances successives de 10 pour en faire 50, 500, 5 000 et 50 000.

Texte comptable en numération acrophonique, vers 329 avant notre ère.

Dans le texte ci-dessus, on lit par exemple à la huitième ligne ΔΔΔΔΜΜΜΜ, représentant 40 040. Ce système, qui a eu cours dès le V^e siècle avant notre ère, servait essentiellement à représenter des poids et mesures, des capacités ou des unités monétaires.

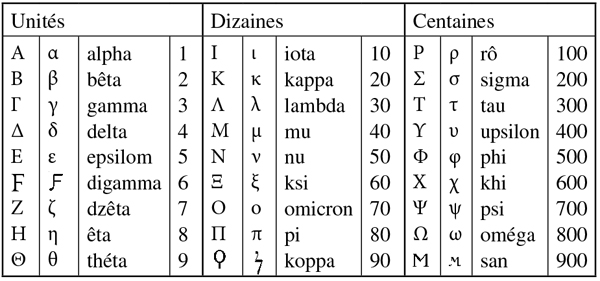
Les nombres alphabétiques grecs.

Plus récent est le système alphabétique, où les nombres sont désignés par les lettres de l’alphabet… tout simplement dans l’ordre alphabétique ! Les neuf premières lettres sont pour les unités, les neuf suivantes pour les dizaines, les neuf dernières pour les centaines, en ayant recours à trois symboles additionnels (digamma pour 6, qoppa pour 90 et sampi pour 900) puisque l’alphabet grec ne comporte que vingt-quatre lettres.

On avait pris l’habitude, pour distinguer les nombres du texte, de les surligner, mais par la suite, dans les textes imprimés, on a remplacé le surlignage par un genre d’accent aigu (la kéréa) placé à côté du nombre. Ce système, dont on n’a pas retrouvé trace au moment même de l’apparition de l’alphabet, mais un peu plus tard, est plus récent que le système acrophonique et se répand vraiment à partir de la fin du IV^e siècle avant notre ère. Il est encore utilisé en Grèce aujourd’hui, comme nous utilisons les chiffres romains, pour les inscriptions sur les monuments ou la pagination de certains livres.

On retrouve également un système de juxtaposition chez les Romains de l’Antiquité, où, à partir du I^er siècle avant notre ère, les nombres sont représentés par sept symboles en forme de lettres qu’il suffira d’agencer entre eux : I, V, X, L, C, D, M pour 1, 5, 10, 50, 100, 500 ou 1 000. L’écriture, alphabétique elle aussi, qui simplifie en quelque sorte l’écriture grecque des nombres, se fait selon des règles précises : les unités placées après un symbole comme V ou X s’ajoutent à 5 ou à 10, celles qui sont placées avant (à condition d’être en nombre inférieur) s’en retranchent. Ainsi, DCCCXXIX représentera-t-il 829 (500 + 300 + 20 + 9). Ce système a été conservé jusque vers 400.

Les Babyloniens, chez qui l’écriture des nombres est apparue au IV^e millénaire avant notre ère, ont utilisé à partir du II^e millénaire avant J.-C. un système « mixte » de juxtaposition de base 10 pour les nombres de 1 à 59 et de position de base 60 pour les nombres supérieurs. Leurs nombres inférieurs à 60 s’écrivaient en utilisant un clou (  \( \mathbf{\top}\)  ) pour l’unité et un chevron (  \( \mathbf{<}\)  ) pour la dizaine, jusqu’à cinq dizaines. Ils pouvaient ainsi les écrire tous avec au plus cinq chevrons et neuf clous.

Comme il existait des risques de confusion, par exemple entre  \( \mathbf{\top}\) \( \mathbf{\top}\)   , qui désignait 61, et  \( \mathbf{\top}\kern-2pt\mathbf{\top}\) , qui désignait 2, on avait imaginé vers –400 un signe de séparation, comme pour distinguer 17 de 107. En Mésopotamie, entre le Tigre et l’Euphrate, à cette date, on avait donc déjà conscience de la nécessité du zéro.

Tablette babylonienne : recueil de problèmes.

C’est aussi lorsqu’on a commencé des pratiques arithmétiques, c’est-à-dire des opérations entre les nombres, malgré l’ingéniosité des scribes ou des comptables, que l’on a compris que ces systèmes juxtaposant les nombres étaient lourds à manipuler, surtout pour les multiplications ; en outre, ils ne permettaient pas facilement d’exprimer de grands nombres.

 
Zéro, ce n’est pas rien !

Le progrès est venu d’Inde, avec deux apports essentiels : la numération de position, où la valeur de chaque chiffre est différente selon sa position dans l’écriture du nombre, et l’apparition du zéro. Les Babyloniens, vers –400, avaient déjà eu conscience de la nécessité de distinguer une place vacante dans l’écriture d’un nombre mais la plus vieille trace d’utilisation du zéro en tant que tel remonte au III^e ou IV^e siècle avant notre ère, sur le manuscrit de Bakhshali découvert au Pakistan en 1881. Ainsi, le système de numération décimale de position que nous utilisons aujourd’hui, comptant les chiffres de 0 à 9, fut-il développé en Inde entre –300 et +600.

On trouve le principe d’une numération de position chez Aryabhata (V^e siècle) et Brahmagupta (598–668), célèbre mathématicien et astronome, énonce des règles de calcul avec le zéro, défini comme la somme d’un bien et d’une dette, deux quantités « opposées ».

La notation indienne, d’abord adoptée par les astronomes arabes, s’est répandue dans le monde méditerranéen, en particulier grâce au livre du mathématicien persan ibn Musa al - Khwarizmi (790–850) Livre de l’addition et de la soustraction d’après le calcul des Indiens. La notation « indo-arabe », mais pour les chiffres seulement, se répand ensuite  en Occident, entre autres grâce à Gerbert d’Aurillac (vers 945–1003). Devenu pape sous le nom de Sylvestre II en 999, ce passionné de mathématiques introduit un abaque d’un genre renouvelé utilisant ces nouveaux chiffres.

Pourtant, même après ce pape mathématicien, la numération de position a mis du temps à s’imposer en Europe. Quand, en 1202, paraît le Liber Abaci où le mathématicien italien Léonard de Pise présente les chiffres arabes et la numération de position, le système de calcul par abaque a encore largement cours et une querelle va opposer les abacistes, tenants de ce calcul « à l’ancienne », avec des tables et des jetons, et les algoristes, partisans des calculs selon les méthodes d’al-Kharizmi.

Évolution de la forme des chiffres d’après Jean-Etienne Montucla (1758).

Avec l’arrivée du zéro, on est entré dans l’ère moderne de la numération décimale de position, et même si la forme des chiffres a un peu été modifiée au fil des siècles, le principe de leur disposition ne variera plus depuis al-Khwarizmi. Tout est prêt maintenant pour la seconde découverte arithmétique de l’humanité : le calcul.