
C'est un paradoxe : l'analyse factorielle des correspondances a été créée par Jean-Paul Benzécri, un mathématicien qui voulait lutter pour des raisons philosophiques contre la pratique des sciences humaines, qu'il jugeait dans les années 1970 pervertie par des options politiques de gauche. Or, le propagateur le plus efficace de cette méthode a été Pierre Bourdieu, qui politiquement se trouvait aux antipodes du mathématicien. Benzécri en effet a construit sa méthode afin de pouvoir examiner des données sans a priori, en substituant au sens commun (et aux orientations politiques des chercheurs) des facteurs définis statistiquement et qui s'imposent par leur neutralité et leur force d'exposition.
Une telle méthode avait de quoi séduire les institutions de recherche qui, comme l'Institut national de la statistique et des études économiques (Insee), avaient vocation à produire des analyses des données officielles qui soient neutres du point de vue politique. Un certain nombre d'élèves de Benzécri importeront sa méthode à l'Insee et en deviendront les propagateurs. L'un d'eux, Alain Darbel, qui avait connu Pierre Bourdieu en Algérie, travailla avec lui pour une enquête sur l'art et les musées et lui fit découvrir l'intérêt de la méthode. Dans ses livres et dans la revue qu'il a créée (Les Actes de la recherche en sciences sociales), on trouve de nombreuses analyses factorielles : c'est encore le cas aujourd'hui.
Le trio Brel–Brassens–Ferré
Pour comprendre l'analyse des correspondances, prenons un exemple extrait des données du célèbre livre de Bourdieu La Distinction (Éditions de Minuit, 1979). Dans le cadre d'une enquête portant sur beaucoup de goûts dans divers domaines (peinture, musique, lectures…), il demande à des enquêtés si tel chanteur fait partie de ses chanteurs préférés qui sont ceux des années soixante : Georges Guétary, Luis Mariano, Petula Clark, Charles Aznavour, Johnny Hallyday, Jacques Brel, Georges Brassens et Léo Ferré. Le tableau ci-dessous donne le nombre de fois où un enquêté de chacune des catégories sociales d'analyse (dont les effectifs varient de 52 pour les professions libérales à 287 pour les employés et cadres moyens) dit que le chanteur considéré fait partie de ses favoris, et il peut en avoir plusieurs.
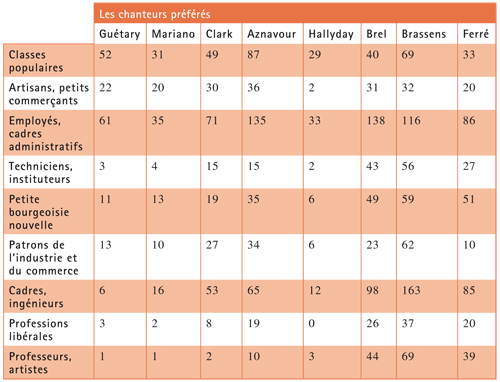
L'analyse des correspondances de ce tableau donne le graphique suivant :
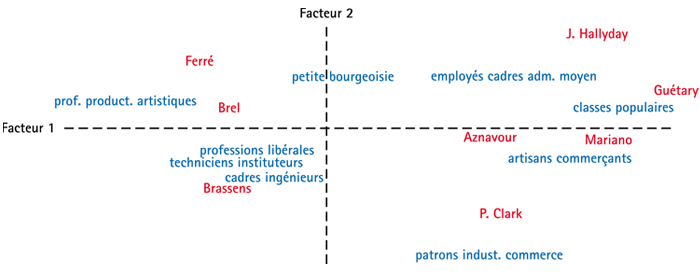
Pour Bourdieu, l'axe horizontal (premier facteur) est interprété en termes de « capital culturel » : à gauche, cette variété de capital est possédée (professeurs et les producteurs artistiques) et à droite, on en est dépourvu (classes populaires). L'axe vertical (deuxième facteur) oppose ceux qui sont dotés d'un « capital économique » (les patrons de l'industrie et du commerce) et ceux qui en sont dépourvus (la petite bourgeoise, les employés et cadres moyens). Ceux qui ont un capital culturel peuvent apprécier des chanteurs comme Ferré, Brel ou Brassens, et c'est ce qui les distingue des autres, tandis que ceux qui en sont dépourvus aiment Johnny Hallyday, Georges Guétary ou Luis Mariano : le registre de la distinction est né du dépouillement de cette enquête par l'analyse factorielle des correspondances.
Comment ce résultat peut-il s'expliquer ? Prenons la proximité entre les points « Ferré » et « Professeurs et producteurs artistiques » : ils sont 39 de cette catégorie à l'apprécier, sur un total (en ligne) de 169 préférences, soit 23,1 %. En tout, 371 préférences se sont portées sur Ferré (total de la colonne) sur un total général de 2 633 (somme de toutes les cases du tableau), ce qui fait qu'en moyenne Ferré est préféré à 14,1 %. Il existe une « attraction » entre Ferré et les professeurs et professions artistiques, car le pourcentage de la ligne est plus élevé que le pourcentage moyen. On peut calculer de même qu'il y a « répulsion » entre Ferré et les classes populaires, puisque celles-ci préfèrent Ferré à 8,5 %, c'est-à-dire moins que la moyenne de 14,1 %. Il en est de même pour les autres points du graphique, avec des situations intermédiaires. Par contre, le choix pour Johnny Halliday de patrons de l'industrie et du commerce est de 3,2 %, légèrement inférieur à la moyenne de 3,5 %.
Ces trois cas de figure sont présentés dans la figure suivante, qui permettra de donner une technique pour lire les analyses factorielles.
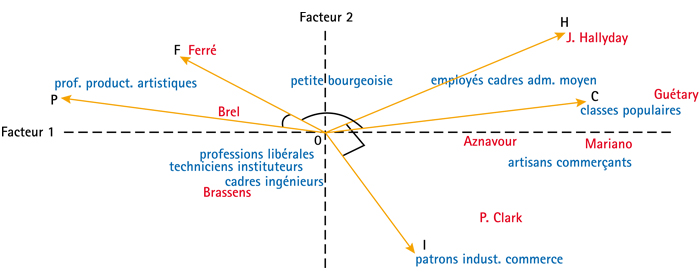
Les vecteurs
Écart à l'indépendance
Sous-jacente à la conjonction, l'opposition ou la quadrature se trouve la notion d'écart à l'indépendance, qui peut être positif, négatif ou nul : faire une analyse des correspondances, c'est prendre pour point de départ le tableau d'effectifs correspondants à l'indépendance.
Simplifions les données précédentes en un tableau à trois lignes grâce à un regroupement par addition (Bourdieu lui-même réalisa un regroupement en trois classes : populaire, moyenne et supérieure) et quatre colonnes (regroupement par « proximité » sur le graphique) : Ferré–Brel–Brassens (colonne A), Hallyday–Guétary (colonne B), Aznavour–Mariano (colonne C), Clark seule (colonne D). Le tableau T de données avec ses marges est le suivant :
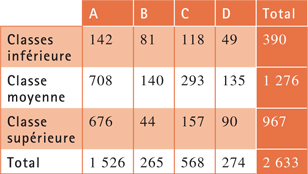
On en déduit le tableau correspondant à la situation d'indépendance : la proportion moyenne de la colonne A est 1 526 / 2 633. Si elle s'appliquait aux 390 classe supérieures, l'effectif correspondant (dit théorique) serait de 390 1 526 / 2 633 soit 226,0 (c'est le produit des marges par le total). On arrive au tableau T0 suivant d'indépendance :
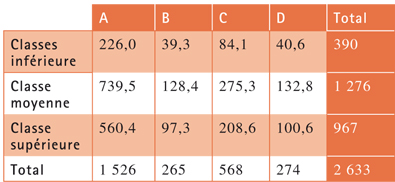
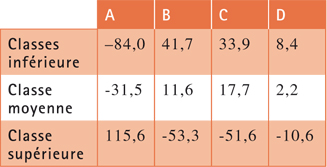
La situation d'indépendance est une référence, non un résultat : l'information pertinente se trouve dans les écarts à l'indépendance, obtenu par soustraction entre le Tableau T et le tableau T0. C'est dans ce premier reste R1 que se trouve toute l'information pertinente.
Un algorithme itératif cherche le couple (ligne ; colonne), noté F1, qui, par multiplication terme à terme, donne le tableau « le plus proche » de R1. On obtient un premier résultat, T1.
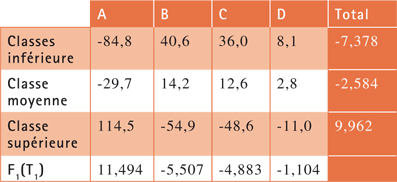
La décomposition n'est pas terminée (il s'en faut d'un dernier reste) car T1, bien que « très proche » de R1, ne lui est pas identique. Ce correctif est obtenu par soustraction entre R1 et T1. On obtient R2, qui est très faible d'importance. Resoumis au même algorithme, il redonne lui-même par multiplication terme à terme de F2, second facteur. C'est la fin de la décomposition.
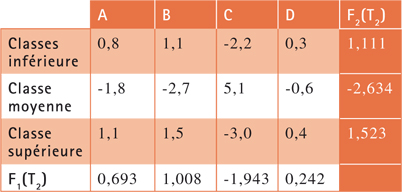
On a ainsi obtenu T – T0 = R1, puis R1 donne F1, dont on tire T1. Ensuite, R1 – T1 = R2, puis R2 donne F2, et enfin un reste nul, qui marque la fin de la décomposition. Une analyse des correspondances extrait des écarts à l'indépendance un premier facteur, qui est le plus important et « le plus proche possible » (au sens de la somme des valeurs absolues des écarts) des écarts d'origine. L'exactitude de ce premier facteur est corrigée par un deuxième. Le nombre de facteurs nécessaires est donné par la plus petite dimension du tableau. Comme T est de rang 3, somme des trois tableaux T0 + T1 + T2, on a donc deux facteurs. L'analyse factorielle des correspondances transforme un tableau quelconque en une somme de tableaux de rang 1, classés par ordre d'importance. Chacun est synthétisé par un couple de vecteurs lignes et colonnes qui permettent une représentation graphique. Dans le cas des grands tableaux, on ne s'intéresse donc qu'aux premiers facteurs, qui sont examinés par ordre d'importance décroissante.
La fin d'une spécificité française
L'analyse des correspondances a été adaptée pour traiter non plus seulement des tableaux de contingence, mais aussi des données d'enquête ou des données lexicales. Elle a certes été reconnue par des chercheurs anglo-saxons mais ne s'est pas imposée comme une méthode de base (contrairement à la France). Du fait de la mondialisation des échanges, l'Insee a donc progressivement renoncé à cette méthode pour se tourner, sur ce type de données, vers les méthodes anglo-saxonnes à base de régression. On a vu ainsi apparaître successivement la régression logistique et les modèles log-linéaires, où l'on arrive avec diverses contorsions à faire de la régression sur des tableaux de contingence. Ces méthodes s'imposent aujourd'hui dans l'Hexagone à côté de l'analyse factorielle : celle-ci est descriptive, les méthodes de régression permettent de faire de la statistique inférentielle.