La théorie des six poignées de main 

Sur les réseaux sociaux, généralistes comme FaceBook ou professionnels comme LinkedIn, on peut définir une distance relationnelle en considérant le réseau comme un graphe. Les nœuds de ce graphe sont les individus du réseau, et deux individus sont reliés par une arête s'ils sont en relation directe.

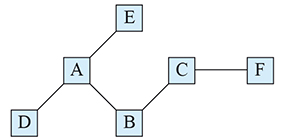
Dans le petit réseau ci-dessus, la distance entre A et B est égale à 1, celle entre A et C égale à 2 et celle entre A et F, égale à 3. En 1929, l'écrivain hongrois Frigyes Karinthy (1887-1938) avait affirmé, quoique de façon plus littéraire, que la distance entre deux personnes n'était jamais supérieure à 6 dans un tel graphe. Cette idée porte le nom de théorie des six poignées de main. Elle se vérifie approximativement sur les réseaux sociaux et dans le fameux (pour les mathématiciens !) nombre d'Erdős, où les relations sont la signature en commun d'un article. Dans ce cas, on ne connaît personne, parmi les gens ayant cosigné un article de mathématique, éloigné de plus de 7 d'Erdős lui-même. Ce monde est petit, et les autres aussi !

Les femmes douées pour les mathématiques 

Les femmes nulles en maths ? est le titre d'un article éclairant sur le rapport entre les maths et les femmes paru dans le numéro 84 de Cerveau et Psycho (janvier dernier). Le titre de la couverture, Femmes et Maths : stop au complexe d'infériorité, résume le sujet. On y apprend le poids des stéréotypes : un sondage de 2015 montrait que 67 % des hommes pensaient que les femmes n'ont pas les capacités pour devenir scientifiques de haut niveau. Peut-être plus grave, le même sondage montrait que 66 % des femmes le pensaient aussi ! Ces stéréotypes poussant les femmes à s'autolimiter.

Or, la plupart des études montrent que les femmes ne sont pas moins douées pour les sciences que les hommes. En outre, plus le niveau en maths des hommes et des femmes est comparable, plus les sociétés sont égalitaires. Donc n'hésitez pas à confier votre magazine favori à vos filles ! 

Le paradoxe de Toscane 

Cosme II de Médicis (1590-1621), grand duc de Toscane, avait remarqué qu'en jetant trois dés, le total 10 sortait plus souvent que le 9. Pourtant, il existe autant de façons de décomposer 9 et 10 en somme de trois nombres entre 1 et 6, ce qui lui semblait contradictoire. Galilée, qui fut son précepteur, trouva la raison de cette bizarrerie, connue depuis sous le nom de paradoxe de Toscane. On peut comprendre son mécanisme en considérant le jeu de pile (P) ou face (F). Si la pièce n'est pas pipée, la probabilité d'obtenir pile est égale à 1/2 (et de même pour face). Si on joue deux fois de suite, chacune des possibilités P–P, P–F, F–P et F–F est équiprobable donc leurs probabilités sont toutes égales à 1/4. Si on jette les deux pièces à la fois, les probabilités d'avoir deux piles ou deux faces sont égales à 1/4, mais celle d'avoir un pile et un face est égale à 1/2 car elle regroupe les deux cas P–F et F–P.

Il en va exactement de même dans le paradoxe de Toscane. Les décompositions de 9 et 10 ne sont pas équivalentes de ce point de vue. La différence tient en la décomposition de 9 en trois fois le même nombre, 3, ce qui est impossible pour 10. La probabilité d'obtenir 9 est égale à 25/216 alors que celle d'obtenir 10 est égale à 27/216, soit 1/8. Ces deux nombres montrent que Cosme était fin observateur, et vraiment très grand joueur, car les probabilités ne diffèrent que de 1 %…