Qui n'a jamais entendu parler des réseaux sociaux ? En France, ces deux termes incluent des supports techniques et informatiques de communication (Facebook, Twitter…), qui n'en recouvrent pas toute l'étendue sociologique. Prenons un peu de hauteur pour revenir au sens, plus général, de système formé par les liens entre des personnes. Le mathématicien voit alors deux types de représentations de ces objets : les graphes et les matrices. Soit les individus sont modélisés par des points (sommets) et les liens par des flèches (arcs) ou des lignes non orientées (arêtes), et on constitue alors un graphe. Soit on choisit la représentation duale, dans laquelle les individus sont représentés par des lignes et des colonnes d'une matrice : deux individus i et j en interaction génèrent un 1 à l'intersection de la ligne i et de la colonne j (et à l'intersection de la colonne i et de la ligne j), et un 0 sinon ; on obtient une matrice d'adjacence.

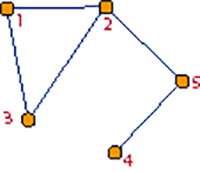
Exemple de réseau social
sous la forme d'un graphe…

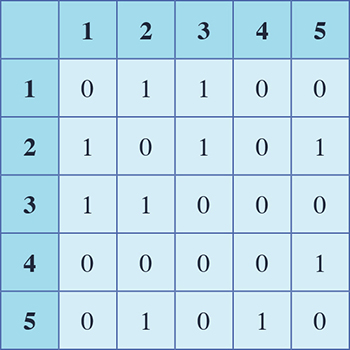
… et sa matrice d'adjacence associée.

Représenter une population nombreuse

La représentation graphique peut sembler séduisante, mais si l'on a une population nombreuse, l'image devient vite inextricable. De plus, l'interprétation qu'elle peut suggérer dépend beaucoup de la façon dont on place les points (très éparpillés ou, au contraire, ramassés). C'est pourquoi les analyses de réseaux se pratiquent à partir de la représentation matricielle.

Beaucoup d'études des réseaux sociaux se concentrent sur les relations interpersonnelles qu'entretiennent des individus choisis selon des règles classiques d'échantillonnage. On estime en général à moins de cinq les quelques intimes auxquels on se sent prêt à confier des choses importantes. On passe à une quinzaine de personnes en ajoutant ceux à qui l'on parle régulièrement au cours d'un mois, quarante à cinquante relations en incluant aussi des personnes que l'on fréquente dans diverses activités, cent à deux cents liens en prenant en compte les personnes que l'on voit peu mais à qui l'on pourrait demander de nous présenter à quelqu'un d'autre, et enfin plus d'un millier de personnes en intégrant les personnes rencontrées au cours de notre vie, dont nous connaissons le nom et que nous pourrions simplement contacter sur la base d'interactions passées.

On s'intéresse ici au cas où l'on traite une ou plusieurs relations sur une population donnée. Le concept le plus important pour les sociologues est probablement celui d'équivalence structurelle. Au sens strict, deux individus sont équivalents dans un réseau s'ils ont exactement les mêmes relations avec les autres. Mais ceci ne se produit pratiquement que lorsque les liens sont dictés par une règle (ainsi, les hommes de troupe dans l'armée sont en situation d'équivalence par rapport à tous les gradés). Mais on se trouve souvent dans des situations où l'équivalence est seulement approximative, ce que l'on mesure sur la base d'un critère statistique.

Supposons que l'on observe trois types d'échange entre les membres d'une organisation : la coopération dans le travail (notée W), l'amitié (A), et l'échange de conseils (C). À chacun de ces types d'échange correspond une matrice d'incidence de taille n s'il y a n employés dans l'organisation. En les juxtaposant, on construit ainsi une matrice à n lignes et 3n colonnes qui pourrait ressembler à celle-ci :

Sur cette base, il est possible de définir la ressemblance entre deux individus i et j, du point de vue de leurs relations, au moyen d'un indicateur de similitude, par exemple le nombre de 1 dans les deux lignes i et j. On engendre ainsi une matrice de similitude, de coefficients s_i,j, à n lignes et n colonnes. Dans notre exemple numérique, on a s_1,2 = 5 et s_1,5 = 4.

Cette matrice peut être analysée par des méthodes classiques en statistique, comme la classification hiérarchique. Ceci permettra de mettre en évidence des « blocs », c'est-à-dire des ensembles d'individus qui ont des rôles semblables dans l'organisation. Étant donné que l'on s'est intéressé à des échanges plutôt informels, ceux-ci ne reflèteront pas forcément ce que prévoit l'organigramme, mais ils seront néanmoins révélateurs du fonctionnement réel de l'organisation.

Un cas particulier important est l'équivalence régulière. Deux individus sont en situation d'équivalence régulière s'ils ont le même type de lien avec d'autres individus qui, eux aussi, partagent le même lien. Intuitivement, les médecins sont régulièrement équivalents parce qu'ils ont le même type de lien (le soin) avec ceux que l'on appelle les patients qui, eux aussi, sont régulièrement équivalents dans ce rapport. Chaque médecin est en relation de soin avec au moins un patient et chaque patient est en relation de soin avec au moins un médecin… sinon on ne lui donne pas ce qualificatif de patient ! Cela se traduit par le fait que, dans la matrice qui représente les relations de soin, l'équivalence régulière se caractérise par l'existence d'un bloc régulier non diagonal tel qu'il y ait un 1 au moins dans chaque ligne et dans chaque colonne.

Les équivalences régulières représentent des rôles sociaux qui lient deux classes : médecins/patients, employeurs/employés, enseignants/élèves…

Détecter les communautés, les leaders…

Des individus tous reliés deux à deux forment une clique. Cela traduit l'idée d'un groupe où tout le monde se connaît. Une clique se représente dans la matrice d'adjacence par un bloc diagonal rempli de 1 (éventuellement après permutation des lignes et des colonnes). Dans notre petit réseau, les sommets 1, 2 et 3 constituent une clique. Mettre en évidence toutes les cliques d'un réseau nécessite un algorithme efficace ; il reste d'ailleurs d'importantes questions théoriques sur la complexité des algorithmes de reconnaissance de cliques dans un graphe (voir Les Graphes, Bibliothèque Tangente 54, 2015).

Les communautés sont quant à elles des groupes homogènes relativement à leur environnement. Pour les repérer, on peut par exemple calculer un degré d'intermédiarité de chacun des liens. Intuitivement, un lien a un degré d'intermédiarité d'autant plus fort qu'il est plus souvent un passage obligé entre deux individus. En supprimant les liens qui ont les plus forts degrés d'intermédiarité, on met en évidence des groupes qui ne sont reliés entre eux que par des ponts. Dans notre réseau, c'est l'arête 2–5 qui a le plus fort degré d'intermédiarité. En la supprimant, on met en évidence deux communautés, {1, 2, 3} et {4, 5}, qui dans ce cas particulier sont aussi des cliques. Cliques et communautés permettent d'aborder la question des zones denses dans les réseaux.

Quels sont les individus que l'on peut considérer comme ayant une position remarquable dans le réseau ? Cela amène à plusieurs définitions de la centralité.

• Quelle est la popularité d'un individu A (souvent appelé Ego) ? On mesure cette notoriété par le rapport du nombre d'individus liés à Ego (on les appelle les Alters) au nombre total possible. Si n est la taille de la population et k le nombre d'Alters, on obtient k / (n × (n – 1)) si le réseau est orienté, 2k / (n × ( n – 1)) s'il ne l'est pas.

• Dans quelle mesure un individu est-il un intermédiaire obligé ? Pour l'évaluer, il faut repérer les géodésiques, c'est-à-dire les chemins les plus courts entre tous les couples d'individus. Un individu est d'autant plus central du point de vue de l'intermédiarité qu'il est sur un plus grand nombre de géodésiques entre tous les couples d'autres individus. C'est-à-dire qu'il est un intermédiaire obligé pour que deux autres personnes puissent se connecter. C'est un indicateur qui est utile lorsque l'on étudie la circulation de l'information dans un groupe.

• Peut-on de même approcher un peu plus l'idée (assez vague et subjective) du pouvoir d'un individu dans un réseau ?

On peut définir également d'autres indices de popularité ou d'influence en traduisant l'idée qu'un individu est d'autant plus central que ceux auxquels il est lié ont eux-mêmes une position plus centrale. C'est un peu l'idée qui se cache derrière le moteur de recherche Google (voir Tangente SUP 77–78, 2014). En notant C_i le degré de centralité de l'individu i et r_i,j les éléments de la matrice R des liens, on peut donc écrire

\( C_i=\sum\limits_{i=1}^n\sum\limits_{j=1}^nr_{i,j}C_j.\)

La valeur de la centralité des individus est donnée par sa coordonnée sur le vecteur propre correspondant à la plus grande valeur propre de la matrice R.

Enfin, il est possible d'apprécier comment un individu peut jouer sa propre partition dans un réseau. Sans rentrer dans les détails du calcul, l'idée est que l'entretien d'une relation a un coût. Si l'on entretient des relations avec des gens qui sont liés entre eux, on risque d'avoir de la redondance dans les informations qu'ils peuvent nous apporter, ou les soutiens dont ils peuvent nous faire bénéficier. De plus, le fait qu'ils communiquent entre eux fait que l'on est moins libre d'adopter des attitudes différentes avec chacun d'eux, ce qui limite notre autonomie d'action. On calcule ainsi un indice de contrainte c_i,j pour l'individu i par rapport à l'individu j, fondé sur la redondance des liens qu'il entretient avec les autres :

\( c_{i,j}=\Big(r_{i,j}+\sum_{\substack{1\leq q \leq n \\ q\neq i, q\neq j}}r_{i,q}r_{q,j}\Big)^2.\)
  

Pour avoir une mesure de la contrainte de i pour tout le réseau, il suffit de sommer les coefficients c_i,j sur j.

Tous ces indicateurs peuvent entrer dans le concept de « capital social » que Pierre Bourdieu avait proposé, en complément à ceux de capital économique et de capital culturel. Ils constituent des solutions apportées par les mathématiques à des questions posées en termes strictement sociologiques.