Imaginons un individu, le décideur, amené à effectuer des choix concernant plusieurs actions potentielles rassemblées dans un ensemble (fini) A : les éléments de A peuvent être des produits, des personnes, des catégories sociales, des stratégies de marketing…

Le décideur se réfère à un seul critère bien déterminé (par exemple, le prix ou encore la quantité lorsque les actions sont des biens achetés, une qualité physique ou psychologique pour des personnes…). Par rapport à ce critère, et pour tout couple (a, b) de deux éléments de A, il est capable d'émettre un et un seul des jugements suivants :

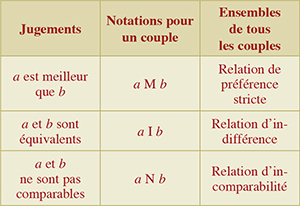
Conformément à l'intuition, on admet généralement que M est transitive (si a est meilleur que b et b meilleur que c, alors a est meilleur que c), I est réflexive (a est équivalent à a) et symétrique (si a est équivalent à b, alors b est équivalent à a), N est symétrique. En outre, les trois paires formées par deux des ensembles M, I et N sont deux à deux disjointes. Modulo d'autres hypothèses techniques, le triplet (M, I, N) définit alors une structure de préférence sur A. La réunion des seules relations M et I permet de définir une relation de préférence.

Les joies de la décision collective

Un cas particulier intéressant est celui où tout ce qui doit être jugé peut être classé. De fait, la connaissance d'un classement des éléments d'un ensemble permet de leur associer un score (le rang dans le classement). Mais lorsque plusieurs décideurs ont affaire à un même ensemble d'actions possibles, la question se pose de traduire la volonté générale en tenant compte des préférences individuelles. C'est une question essentielle dans toute société démocratique. Ne suffit-il pas alors de demander aux décideurs de classer les actions et de retenir, comme choix collectif, l'option qui a récolté le meilleur « classement global » ? Ce procédé élémentaire convient lorsqu'il n'y a que deux actions. Dès que le nombre de décideurs dépasse 2 et que le nombre d'actions dépasse 3, des choix individuels cohérents peuvent donner naissance à un choix collectif incohérent. En termes mathématiques, le choix collectif n'est pas transitif, même si les choix individuels le sont. Ce paradoxe a été découvert par le marquis de Condorcet en 1785 et porte son nom.

Qu'à cela ne tienne : il suffit de rechercher quelles règles doivent être édictées pour éviter cet effet Condorcet. Cette question a été étudiée par le mathématicien Kenneth Joseph Arrow dans son livre Social Choice and Individual Values, paru pour la première fois en 1951 ; ce travail valut à son auteur de recevoir le prix Nobel en sciences économiques en 1972. Le résultat principal de Arrow, connu sous le nom de théorème d'impossibilité d'Arrow, est surprenant, voire inquiétant : il est logiquement impossible d'agréger « de façon démocratique » (en respectant des règles reconnues dans tout système démocratique) des préférences individuelles en un choix collectif rationnel. Ce résultat d'impossibilité est démontré !

Comme l'a écrit Paul Samuelson, également prix Nobel en sciences économiques (en 1970) :

« La démocratie parfaite, à laquelle tant de grands esprits de l'histoire ont rêvé, n'est qu'une chimère logiquement auto-contradictoire. Aujourd'hui, les chercheurs du monde entier, en mathématiques, en politique et en économie, essaient de sauver ce qui peut l'être du “désastre” provoqué par la découverte d'Arrow. »

Même si le théorème d'Arrow montre l'impossibilité d'obtenir en toutes circonstances un choix collectif incontestable en exploitant les préférences individuelles, des méthodes comme Electre peuvent aider à fournir une solution pratique. Electre (pour Élimination et choix traduisant la réalité) a été mise au point par des chercheurs français dirigés par Bernard Roy durant la seconde moitié du XX^e siècle. On s'intéresse au cas de n décideurs. Les actions potentielles a, b… sont classées avec possibilité d'ex-aequo, pour chaque individu i, selon une relation de préférence au sens large (au moyen d'une relation P_i = M_i ou I_i). Pour tout couple (a, b) composé de deux actions distinctes, on construit les ensembles D⁺(a, b) = {i tels que a M_i b}, D^–(a, b) = {i tels que b M_i a} et D = (a, b) = {i tels que a I_i b}. Il s'agit donc des ensembles indiquant les décideurs qui estiment que, respectivement, l'action a est meilleure que b, l'action b est meilleure que a, les actions a et b sont équivalentes.

Un problème de poids

Le décideur i se voit attribuer un poids p_i d'autant plus grand que sa voix est jugée importante (si tous les décideurs ont le même pouvoir, ils reçoivent un même poids, par exemple p_i = 1). On calcule ensuite, pour tout couple (a, b), les nombres P⁺(a, b) et P⁼(a, b), qui représentent respectivement les sommes des poids p_i lorsque i parcourt D⁺(a, b) et D⁼(a, b). On évalue leur somme c (a, b) = P⁺(a, b) + P⁼(a, b). Si c (a, b) est « grand », l'action a sera probablement préférée collectivement à b. De façon plus rigoureuse, on introduire un seuil de concordance k dont une valeur adéquate est déterminée par l'expérience. On dit alors que a l'emporte sur b au seuil k (ou que a surclasse b) lorsque c (a, b) est supérieur à k.

On considère ensuite le graphe G = (A, S), appelé le graphe de surclassement, dont l'ensemble A des sommets est composé de toutes les actions potentielles, un arc reliant un sommet a à un autre b si, et seulement si, a est surclassé par b, ce qui se note a S b. Le choix collectif peut se faire en sélectionnant des actions après avoir éliminé celles qui sont « peu intéressantes » (on retient les actions qui ne sont pas directement comparables entre elles et telles que toute action éliminée est surclassée par au moins une action conservée).

Le formalisme semble technique en apparence, mais Electre s'implémente très aisément. Prenons trois personnes, I, J et K, qui ont à choisir entre quatre actions a, b, c ou d. I, J et K n'ont pas la même importance : leurs préférences sont pondérées par les poids p_I = 1, p_J = p_K = 2. Une action reçoit le score de 1 lorsque la préférence est jugée « faible », le score de 2 pour une préférence « moyenne », le score de 3 pour une préférence « forte ». Après consultation de I, J et K, l'action a se voit attribuer le score de 2 pour chacun des décideurs, b reçoit 1 de I et K et 2 de J, c obtient 1 de I et 3 de J et K, et enfin d reçoit 2 de I et J et 3 de K. On peut alors construire les tableaux suivants, puis le graphe de surclassement au seuil k = 4 :

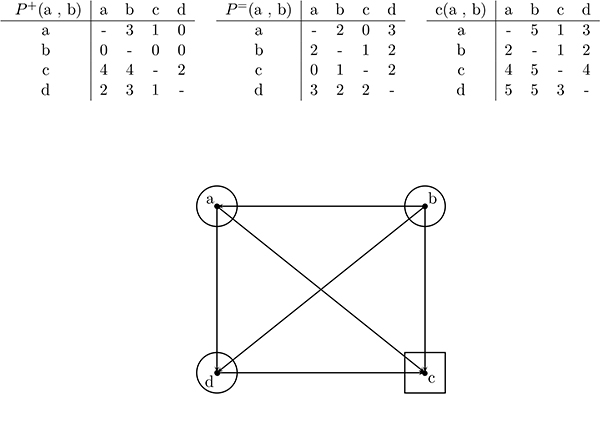
Pour ce graphe de surclassement, le sommet c surclasse tous les autres. En conséquence, le choix collectif se portera idéalement sur cette action c.

Bien entendu, tous les cas pratiques ne sont pas aussi évidents. La méthode Electre permet cependant d'éliminer de manière efficace des actions peu pertinentes, ce qui fournit déjà une aide conséquente pour une décision collective judicieuse.