Tout fournisseur doit avoir accès à la commande publique, réglementée par le droit des marchés publics, qui cherche en priorité à éviter tout favoritisme. Le Code des marchés publics subit de régulières modifications à la recherche d'un difficile compromis entre une liberté de choix et un carcan méthodologique, pour assurer une bonne utilisation des deniers publics.

Les règles du jeu

L'article 53 de ce Code stipule que le marché doit être attribué à l'offre la plus avantageuse, en se fondant sur des critères non discriminatoires, et si jamais le critère est unique, ce ne peut être que le prix (dans le cas de produits normalisés, par exemple). Pourtant, en toute rigueur, le Code n'oblige pas l'acheteur public à retenir le prix parmi l'ensemble des critères qualifiant l'offre. Mais, comme le précise le guide associé, la qualité d'une offre ne peut être indépendante du prix, critère inévitable implicite. Le prix est donc imposé dans un cas, mais ne l'est pas dans un autre (multi-critères). Ce manque de rigueur a de quoi surprendre…

Il est déconseillé, en général, de recourir au critère unique du prix, et la jurisprudence a notamment retenu que c'était illégal dans le cas de travaux complexes. Considérons donc le cas de deux critères, financier et technique. Se pose alors le problème de donner une note à chacun de ces critères pour déterminer la note finale, avec de possibles coefficients de pondération.

Dans le cas d'un marché très technique (comme l'élaboration d'un logiciel informatique complexe) ou potentiellement dangereux (des explosifs, des médicaments…), il devrait aller de soi que le poids technique l'emporte sur le poids financier, ce qui est loin d'être le cas dans la pratique ! Alors que la rigueur caractérise le domaine technique, la pondération attribuée à chaque partie de l'offre technique pour établir une note globale ne peut échapper à une part de subjectivité. À l'opposé, le prix, dont la détermination est libre, produit une note « objective » à l'aide d'une formule. Mais une inévitable subjectivité se cache cependant dans le libre choix de cette formule. Et le fait qu'il n'existe pas de référence absolue explique la grande profusion de formules mathématiques de notation du critère prix, plus ou moins complexes, utilisant des droites, mais aussi des hyperboles, paraboles, exponentielles, logarithmes, fonctions homographiques…

Le guide des marchés publics présente un nombre volontairement limité de méthodes de notation, qui se doivent d'être simples et compréhensibles par tous les opérateurs économiques. Il rappelle en particulier qu'il est illégal d'évaluer les offres en fonction de l'écart à une estimation financière. En effet, si la meilleure évaluation est attribuée à l'estimation, comment peut-on noter une offre qui lui serait inférieure ? De même, il est nécessaire de bannir, lors de la notation des critères, toute méthode ayant pour conséquence une note négative, ou une note supérieure à la note maximum.

Pour des raisons de simplicité, on considère souvent des formules linéaires paramétrées de la forme

\( f_P(P)=N\frac{pP_m-P}{(p-1)P_m},\)

où P est la valeur de l'offre, P_m l'offre la plus basse et f_p (P_m) = N est la note maximale. En toute rigueur, ce qui est rarement le cas, il faut stipuler que f_p (P) = 0 pour P ≥ p × P_m, pour éviter les notes négatives.

Pour p = 2, la formule  

est couramment utilisée, ce qui illustre en fait une curieuse conception des pourcentages (voir encadré). On considère en effet que, puisqu'une offre \( P=P_m\left[1+\frac{P-P_m}{P_m}\right]\)  est \( x=\frac{P-P_m}{P_m}\%\)   supérieure à P_m, alors sa note doit être x% moindre, ce qui induit de potentielles notes négatives. Si les offres sont resserrées, cela a peu de conséquence, mais dans le cas d'un marché complexe, avec une offre conforme mais sous-estimée, on se condamne à un moins-disant mal-faisant.

Autre formule linéaire,

\( d(P)=N\left[1-\frac{P-P_m}{P_M-P_m}\right],\)

 telle que d (P_M) = 0, où P_M est l'offre maximale. Elle présente l'inconvénient d'attribuer systématiquement la note 0 à une offre qui peut très bien être objectivement compétitive.

Une formule similaire,

\( c(P)=N\left[1-\frac{P-P_m}{P_M}\right],\)

est à éviter car elle avantage les offres chères par sa faible décroissance (voir la figure ci-contre). De façon générale, toutes les formules de notation utilisant l'offre la plus chère sont risquées en cas de remise d'offres déraisonnables, mais qui ne peuvent être éliminées pour non-conformité. 

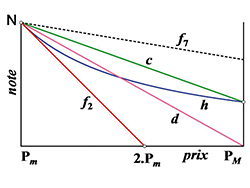
Représentation de différentes fonctions de notation.

La simplicité calculatoire, qui justifie l'année lombarde pour les crédits depuis le Moyen Âge (le calcul des intérêts d'un prêt court sur trois cent soixante jours seulement) et les tranches d'imposition depuis le XIX^e siècle, n'est plus un critère suffisant pour imposer la linéarité à l'ère informatique. La méthode la plus utilisée, et aussi la plus naturelle, est d'attribuer la note maximale à la meilleur offre et une note inversement proportionnelle à leur offre aux autres candidats. La formule est alors

\( h(P)=N\frac{P_m}{P}\)

ce qui correspond à une branche d'hyperbole. Ainsi,

\( c(P_M)=h(P_M)=N\frac{P_m}{P_M}\) .

La droite c (P) est donc la corde de cette branche d'hyperbole. Puisque 

\( f'_2(P)=\frac{-N}{P_m}=h'(P_m),\)

la droite f₂ (P), justifiée par une recette mal comprise, est en fait la tangente à l'hyperbole en P = P_m. Ces explications géométriques ne sont jamais présentées, les formules semblant n'être, dans le monde économique, que des recettes… Cette formule hyperbolique est la méthode la plus simple, la plus neutre, et est recommandée pour la plupart des marchés.

Le jugement du Conseil d'État

Si la jurisprudence est abondante concernant les critères techniques, elle est nettement plus rare concernant le critère prix. Ayant eu à juger, en novembre 2014, de la validité de la formule

\( f'_7(P)=\frac{N}{6}\left(7-\frac{P}{P_m}\right),\)

pour un marché pondérant à égalité les critères prix et technique, le Conseil d'État a considéré qu'il aurait mieux valu attribuer 80 % au critère valeur technique et 20 % sur le critère prix, avec une formule plus classique sur le prix, plutôt que de choisir cette méthode de notation qui, par son arithmétique, neutralise la pondération des critères. Jamais auparavant le Conseil d'État, la plus haute juridiction administrative, n'avait porté une appréciation sur la méthode de jugement du prix ! Il s'agit, comme dans tout domaine législatif, de veiller à ce que l'esprit des lois ne disparaisse pas sous la procédure.