La notion de convexité est omniprésente en économie, qu'il s'agisse de la modélisation financière (évolution d'un capital, valeur d'une annuité, dépendance du prix d'une obligation vis-à-vis du taux d'intérêt…) ou d'autres domaines de la microéconomie et de la macroéconomie. Comment utiliser cette notion dans la modélisation des préférences du consommateur ? En introduisant une structure relationnelle de préférences…

Vous avez dit convexité ?

Si l'on pose la question à un étudiant de lycée, « Qu'est-ce qu'une fonction convexe ? », il y a gros à parier qu'il répondra « une fonction dont la dérivée seconde est positive » ou qu'il esquissera un geste représentant l'allure d'un sourire. La notion de convexité est indépendante de toute propriété de dérivabilité (p&our les fonctions deux fois dérivables, la première réponse est cependant pertinente) et la réponse par geste est plus proche de la définition intrinsèque.

Comment modéliser le comportement d'un consommateur P particulier, un autre pouvant avoir des comportements différents ? Supposons que P a la possibilité d'acquérir différents biens en diverses quantités. Son choix des quantités achetées des biens dépend de ses préférences (ses goûts, ses besoins), des prix unitaires des biens et du budget dont il dispose. L'objectif est donc de modéliser les préférences de P et de déterminer son choix optimal compte tenu du budget disponible. Le nombre de biens disponibles est noté N et n_j représente le nombre d'unités acquises du bien numéro j. Un panier de biens est donc caractérisé par un vecteur (n₁, n₂… n_N). Les économistes spécifient généralement des relations structurelles entre les différents paniers possibles. Il y a ainsi la préférence stricte (A est strictement préféré à B), ensuite la préférence faible (A est au moins aussi préférable que B), et enfin l'indifférence (le bien A a le même niveau de préférence que le bien B). Les propriétés que l'on exige habituellement d'une relation de préférence sont la réflexivité (pour tout bien A, A est au moins aussi préférable que lui-même !) et l'antisymétrie (si le bien A est au moins aussi préférable que B et que B est au moins aussi préférable que A, c'est que A et B ont même niveau de préférence). Il doit également y avoir transitivité : si A est préférable à B et B à C, c'est que A est préférable à C. Enfin, on exige la complétude : il doit y avoir moyen de classer deux biens.

D'un point de vue mathématique, ces exigences font de la préférence une relation de pré-ordre complet, le préfixe « pré » traduisant la possibilité d'avoir des ex-æquo. La relation d'indifférence est réflexive, symétrique et transitive, ce qui fait d'elle une relation d'équivalence. On ajoute encore deux hypothèses qui font intervenir la composition des paniers : la monotonie (le consommateur cherche toujours à consommer plus) et la convexité (qui traduit un attrait pour la diversité : si A est équivalent à B, et que l'on définit \( C=\ell A+(1-\ell)B\) avec \( \ell\) compris entre 0 et 1, alors C sera toujours au moins aussi préférable que A et B). Voilà donc une propriété mathématique interprétée à la fois économiquement et sociologiquement !

Les préférences mises en courbe

Notre consommateur P a deux biens en vue. La plupart des résultats restent valides de manière générale, mais ce cas particulier permet une illustration graphique. Une courbe d'indifférence (appelée aussi isoquante), tracée dans le plan (n₁, n₂), représente l'ensemble des paniers entre lesquels le consommateur est indifférent. On peut aussi la définir géométriquement, comme le lieu des points représentatifs des paniers indifférents à un panier donné. L'ensemble C/I des courbes d'indifférence de P est appelé sa carte d'indifférence. Une C/I partage le plan (n₁, n₂) en deux régions : celle située au nord-est, qui correspond aux paniers strictement préférés à ceux de la C/I, et celle située au sud-ouest, qui correspond aux paniers surclassés par ceux de la C/I. Ceci résulte de l'hypothèse de monotonie. De même, les C/I sont décroissantes. De plus, deux C/I distinctes ne peuvent se croiser ; en effet, le panier A du point d'intersection serait indifférent à deux autres paniers B et C (situés sur chacune des C/I) et, par transitivité, on aurait B équivalent à C, ce qui est impossible puisqu'ils sont situés sur deux C/I distinctes. Enfin, l'hypothèse d'attrait pour la diversité montre que les C/I sont convexes. En résumé, la carte d'indifférence d'un consommateur est constituée d'un jeu de courbes d'indifférence, décroissantes, convexes et « emboîtées ».

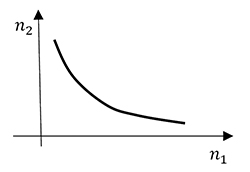
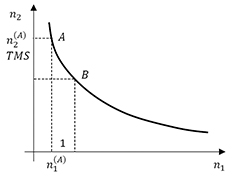
Une telle présentation est relative à des paniers constitués de biens qui sont partiellement substituables. De ce point de vue, deux situations extrêmes peuvent être envisagées. La première concerne les biens parfaitement substituables (comme deux eaux minérales de mêmes caractéristiques) : le consommateur est prêt à substituer un des biens par l'autre ; les C/I sont alors des segments de droite. À l'opposé, pour les biens parfaitement complémentaires (un soulier gauche et un soulier droit), le consommateur n'acquerra jamais un bien sans l'autre puisque aucune substitution n'est possible ; les C/I ont alors la forme d'un L. L'outil utilisé par les économistes pour mesurer cette substituabilité est le taux marginal de substitution (TMS). Pour un panier initial A, on définira le TMS comme la quantité du bien numéro 2 que le consommateur est prêt à abandonner pour acquérir une unité supplémentaire du bien numéro 1, le consommateur étant indifférent entre le panier transformé et le panier initial. Le TMS se définit donc implicitement en disant que le consommateur est indifférent entre le panier A = (n₁^(A), n₂^(A)) et le panier B = (n₁^(A) + 1, n₂^(A) – TMS). Un mathématicien préférera envisager le rapport (au signe près) de la variation en ordonnée et de celle, en abscisse, qui l'a provoquée ou, mieux encore, la limite de ce rapport des variations :

\( TMS=\lim_{\Delta n_1 \to 0}\left(- \frac{\Delta n_2}{\Delta n_1} \right)\)

Il s'agit donc de la pente (au signe près) de la tangente à la C/I au point A. En raison de la convexité des C/I, le TMS décroît au fur et à mesure que le choix se déplace sur la C/I vers le sud-est. De plus, pour des biens parfaitement substituables, le TMS est constant (et est égal, au signe près, à la pente du jeu de droites qui constituent la carte d'indifférence) et, pour des biens parfaitement complémentaires, le TMS n'est pas défini.

La notion d'utilité 

La fonction d'utilité u d'un consommateur attribue une valeur numérique à chaque C/I, et donc à chacun des paniers de biens qui la composent ; elle a pour objectif de refléter le classement établi par la relation de préférence et donc de traduire la satisfaction procurée. Pour deux biens A et B équivalents, on doit avoir u (n₁^(A), n₂^(A)) = u (n₁^(B), n₂^(B)) et, pour A préférable à B, u (n₁^(A), n₂^(A)) > u (n₁^(B), n₂^(B)). Les C/I peuvent se déduire de la fonction d'utilité : pour une valeur u₀ donnée de l'utilité, on définira la C/I correspondante par {(n₁, n₂) : u (n₁, n₂) = u₀}. La fonction d'utilité est donc utilisée pour comparer des paniers de biens.

Les valeurs prises par cette fonction n'ont guère d'importance. On peut lui faire subir toute transformation affine croissante sans en altérer l'interprétation. Par contre, les propriétés suivantes, liées à la forme de la fonction d'utilité, sont fondamentales. C'est une fonction croissante de chacun de ses arguments (hypothèse de monotonie) ; c'est une fonction concave de chacun de ses arguments (hypothèse de convexité ; f est concave si – f est convexe) ; le TMS se calcule aisément à partir de la fonction d'utilité. Pour un niveau d'utilité u₀ donné et en passant d'un point (n₁, n₂) à un point « voisin » (n₁ + Δn₁, n₂ + Δn₂) de la même C/I d'utilité u₀, l'évolution de la valeur de la fonction d'utilité est donnée approximativement par le développement de Taylor à l'ordre 1 (voir les boîtes à outils analytiques), soit u (n₁ + Δn₁, n₂ + Δn₂) – u (n₁, n₂) = , et le taux marginal de substitution TMS vaut donc environ

\( -\frac{\Delta n_2}{\Delta n_1} \, \textnormal{ soit environ } \, \frac{u'_{n_1}(n_1,n_2)}{u'_{n_3}(n_1,n_2)}.\)

Les dérivées partielles qui apparaissent représentent la variation d'utilité, exprimée en proportion de la variation de la quantité du bien qui l'a provoquée. Cette quantité porte le nom d'utilité marginale. Le caractère concave de la fonction d'utilité se traduit par le caractère décroissant de l'utilité marginale.

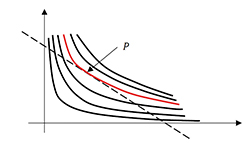
Qu'en est-il du budget ? Étant donnés deux biens, quel panier (n₁, n₂) le consommateur choisira-t-il s'il dispose d'un budget _b limité pour cette acquisition ? Si les prix unitaires des deux biens sont respectivement p₁ et p₂, la contrainte du budget impose que n₁p₁ + n₂p₂ ≤ b. Les paniers satisfaisant à cette contrainte sont donc situés sous la droite d'équation n₁p₁ + n₂p₂ = b. Par ailleurs, le consommateur cherche à maximiser son utilité, c'est-à-dire à choisir un panier situé sur une C/I la plus éloignée possible de l'origine. Vu le caractère décroissant, convexe et emboîté des C/I, le graphique montre que la solution de ce problème est unique et qu'elle correspond à un panier de la droite limitant la zone de contrainte. Le panier idéal est la solution du problème de la recherche du maximum de la fonction d'utilité sous contrainte budgétaire. Or, cette contrainte peut être remplacée par n₁p₁ + n₂p₂ = b, ce qui simplifie l'étude. Lorsque la contrainte est une équation (et non une inéquation), l'outil mathématique pour résoudre ce problème d'optimisation est la classique méthode des multiplicateurs de Lagrange. Cette dernière fournit alors le panier optimal pour lequel les utilités marginales sont proportionnelles aux prix unitaires.