Les échelles semi logarithmiques

Supposons que l'on s'intéresse à la variation de la population de différents pays. Parmi eux, la France et le Gabon ont les tailles qui diffèrent énormément. Mettons en abscisse les années de recensement et en ordonnées la population. Dans un repère habituel, la courbe décrivant la population du Gabon sera écrasée sur l'axe des abscisses, et les variations seront imperceptibles.

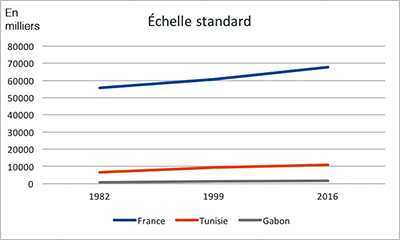
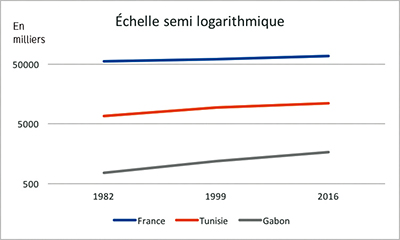
Pour permettre une lecture claire des données, on gradue l'axe des ordonnées suivant une échelle logarithmique ; ainsi, l'écart entre cent mille et un million est le même qu'entre un million et dix millions. Dès lors, la pente des segments de droite de chaque courbe représente l'accroissement relatif, et non absolu.

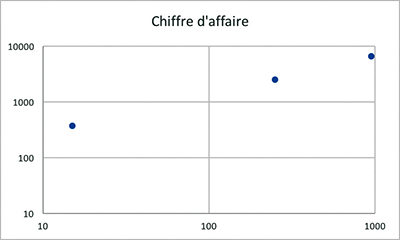
On peut également graduer les deux axes en échelles semi logarithmique. Ceci est intéressant si l'on veut représenter le chiffre d'affaire de plusieurs entreprises de tailles très différentes en fonction du nombre de leurs salariés : cela permet de rendre visible la position des plus petites d'entre elles. Les droites parallèles à la première bissectrice correspondent aux entreprises de même productivité par employé, alors que pour une graduation habituelle, ce sont les droites passant par l'origine.

Dérivée première, dérivée seconde

Pour calculer la variation d'une valeur f(t) par unité de temps entre deux instant t₀ et t, on effectue le rapport d(t) = (f(t) – f (t₀)) / (t – t₀).
Si l'on s'intéresse à une variation instantanée à l'instant t₀, il semble naturel de regarder si ce rapport d(t) admet une limite lorsque t tend vers t₀. Si cette limité existe, on la note f'(t₀₎ et on l'appelle la dérivée de f à l'instant t₀. Lorsque la quantité étudiée correspond à la distance parcourue par un mobile, f'(t₀) n'est autre que la vitesse instantanée, celle que l'on lit sur le compteur de sa voiture.

Posons h = t – t₀, on peut alors écrire  f(t₀ + h) = f(t₀) + h f'(t₀) + h × Ɛ(h), avec Ɛ(h) qui tend vers 0 avec h. Autrement dit, f(t₀ + h) peut être approximé par f(t₀) + h f'(t₀).

Lorsque la fonction représente une variation de valeur par rapport au temps (production, dépense, profit…), la dérivée en un point correspond au taux marginal d'accroissement.

Sur une représentation graphique, f'(t₀) est la pente de la tangente au point d'abscisse (t₀. Si, de plus, la fonction f admet en tout point une dérivée, on peut réitérer l'opération : si la fonction f'(t₀) est dérivable en t₀, cette dérivée s'appelle la dérivée seconde et se note f''(t₀). Dire que la dérivée seconde d'une fonction croissante est positive, ça veut dire que la croissance s'accélère : la concavité de la courbe est tournée vers le haut. Si, au contraire, elle est négative, la croissance se ralentit et la courbe est concave.

Une vision plus intuitive de la dérivée : les accroissements infinitésimaux

La notion d'accroissement infinitésimal est à la base du calcul différentiel. Lorsque Newton et Leibniz l'ont introduit au XVII^e siècle, le sens mathématique leur échappait car ils ne possédaient pas la notion de limite, qui ne fut correctement dégagée qu'au milieu du XIX^e siècle. Cependant, la méthode intuitive qu'ils utilisaient reste intéressante pour comprendre ce concept.

On s'intéresse à une grandeur variable y au cours du temps à l'instant t₀. On la fait varier d'un bref instant, noté ∆t. On note alors ∆f la variation de la grandeur f. Le quotient ∆f / ∆t correspond à la pente de la droite joignant les points d'abscisse t₀ et t. Lorsque t tend vers t₀, on retrouve la dérivée de f en t₀.