Les économistes font très souvent appel au concept d'élasticité, qu'ils préfèrent à la dérivée usuelle. Comment cette notion est-elle apparue ? Et surtout, dans quelles situation l'utilise-t-on ?

Fonction de demande

Pour un produit donné, les quantités qui le caractérisent sont mesurées à l'aide d'une certaine unité, qui peut être la pièce, le kilo ou la tonne. La demande q représente la quantité (que le vendeur espère optimale) achetée pendant une période de référence convenue ; cette quantité dépend évidemment du prix p (sous-entendu de vente et unitaire) du bien, mais aussi d'autres grandeurs : qualité du produit, prix d'autres biens concurrents, de remplacement ou complémentaires, revenu du consommateur… Dans une théorie économique classique, on fait l'hypothèse que le consommateur agit de façon hédoniste et rationnelle. Il cherche en effet à retirer de ses acquisitions la satisfaction la plus grande possible, mais il souhaite aussi respecter ses contraintes budgétaires que lui impose sa part de revenu disponible pour ses achats. Ici, on ne tiendra compte que de l'influence du prix p sur la demande q. La dépendance de q en fonction de p sera supposée connue. D'un point de vue mathématique, on postule l'existence d'une fonction f telle que q = f (p), appelée fonction de demande du produit. On admet que f est positive, définie, continue et dérivable sur l'ensemble des réels positifs. On la suppose de plus décroissante, ce qui est le plus souvent le cas, sauf pour des produits assez exceptionnels comme des produits de luxe ; de fait, un individu est généralement disposé à commander une plus grande quantité d'un produit lorsque le prix s'affaiblit.

Graphiquement, une fonction de demande admet une représentation graphique, nommée tout naturellement courbe de demande. Un exemple de courbe de ce type est tracé ci-dessous en adoptant d'une part le point de vue de l'économiste, et d'autre part celui du mathématicien : le premier place les prix en abscisses et les quantités en ordonnées, alors que le second fait le contraire.

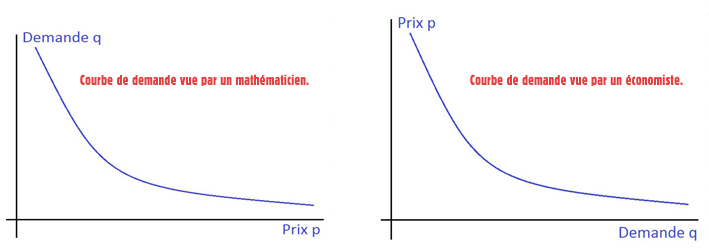
Lorsqu'un prix p augmente d'une quantité \( \Delta{p}\) , la demande devient égale à \( f(p+\Delta{p}).\)  La différence entre les deux demandes correspondant à cette différence de prix est égale à  \( \Delta{q}=f(p+\Delta{p})-f(p+\Delta{p}).\) Est-il possible de « mesurer la sensibilité » de la demande pour une telle variation \( \Delta{p}\) du prix ? On pourrait considérer en premier lieu le rapport des variations  \( \Delta{p/\Delta{q}}.\) Ce rapport correspond graphiquement à la pente de  la corde reliant les deux points de coordonnées \( (p,f(p))\)  et \( (p+\Delta{p}, f(p+\Delta{p}))\)  situés sur la courbe de demande. Cependant, ce rapport n'est guère adéquat : déjà, il dépend des unités adoptées pour les grandeurs p et q (ainsi si une demande est exprimée en tonnes plutôt qu'en kilos, la pente en question est mille fois plus raide, alors que la situation économique est inchangée) ; ensuite, un même rapport peut se référer à des situations bien différentes (lorsque le prix passe de 5 à 6 euros et que, parallèlement, la demande varie de 10 à 8 ou de 1 000 000 à 999 998, le rapport  \( \Delta{p}/\Delta{q}\)  est le même, égal à –2, alors que la demande est plus fortement influencée dans le premier cas (diminution de 20 %) que dans le second (diminution de 0,0002 %). Pour éviter ces deux inconvénients a émergé, au cours du temps (voir l'encadré), le concept d'élasticité de la demande.

Des points et des arcs

Les deux défauts peuvent être évités en travaillant non pas avec les variations absolues  \( \Delta{q}\)  et  \( \Delta{p}\)  de la quantité et du prix, mais avec leurs variations relatives  \( \Delta{q}/q\)  et  \( \Delta{p}/p\) , qui peuvent être exprimées en pourcentages et ne dépendent pas des unités choisies. On considère alors le rapport de ces deux nombres, soit \( (\Delta{q}/q)/(\Delta{p}/p),\) que l'on nomme élasticité de la demande (par rapport au prix) et que l'on peut noter \( E_{q, p, \Delta p}\) . L'élasticité représente le rapport du pourcentage de la variation de la demande sur le pourcentage de la variation du prix ; c'est aussi le quotient de la pente  \( \Delta{q}/\Delta{p}\)  par la valeur moyenne q / p. On appelle cette expression l'élasticité-arc car elle dépend de l'arc situé sur la courbe de demande et compris entre les abscisses p et \( p/\Delta{p}\) . Cette notion est généralement employée en présence d'un cas discret (concrètement, lorsque l'on dispose d'un tableau d'observations donnant les valeurs de la demande q pour différentes valeurs du prix p). Dans le cas continu, où la demande q = f (p) est fournie par une fonction f continue et même dérivable, on remplace l'élasticité-arc par l'élasticité-point

  \( \varepsilon{_{q,p}}=f'(p)/(q/p).\)

En d'autres termes, l'élasticité-point est le rapport entre le nombre dérivé f '(p), encore appelé par les économistes la valeur marginale de la demande, et la valeur moyenne q/p. Ce rapport ne dépend que du point d'abscisse p sur la courbe de demande et non plus de l'arc entre les abscisses p et \( p+\Delta{p}\) . Il peut aussi s'écrire sous la forme équivalente 

\( \varepsilon{_{q,p}}=\dfrac{d \ln(q)}{d \ln(p)}.\)

L'élasticité-point mesure la pente de la tangente à la courbe de demande sur un graphique doublement logarithmique (voir les boîtes à outils mathématique en pages précédentes). Il mesure la façon dont le logarithme de la quantité varie en fonction du logarithme du prix. Comme toujours avec ces derniers, on travaille en variations relatives. Généralement, ces deux élasticité diffèrent, mais sont souvent proches (voir en encadré).

Les économistes contemporains ont largement étendu la portée du concept d'élasticité en l'employant dans d'autres situations que l'étude de la demande. Ils l'appliquent à de multiples fonctions comme l'offre en fonction du prix, le coût de production par rapport à la quantité produite, le revenu du vendeur face au prix, l'emploi par rapport à la demande effective, la production en fonction de la demande… Ils l'envisagent également pour des fonctions de plusieurs variables, en considérant des élasticités partielles, croisées, de substitution. Ils s'intéressent aussi à des situations dynamiques qui tiennent compte des changements intervenus dans le temps. C'est le cas pour l'élasticité d'anticipation des prix, ou pour celle des importations ou des exportations par rapport au prix relatif. Ainsi, de nos jours, le concept d'élasticité est couramment exploité dans de nombreux problèmes rencontrés dans l'univers économique.