Les mathématiques se distinguent des autres sciences par le fait qu'elles sont les seules à apporter des démonstrations de certaines propriétés. L'avantage du raisonnement démonstratif est qu'il est sûr, incontestable et à l'abri de toute controverse, même si ce dernier point ne s'établit pas de manière instantanée (l'exemple de l'introduction des géométries non euclidiennes en atteste). Mais, le temps jouant, tous les esprits éclairés se rendent aux évidences des démonstrations ne comportant aucune erreur logique.

Dans tous les autres domaines scientifiques, modèles et théories sont soumis à une procédure de validation, qui consiste à comparer les résultats issus d'un modèle avec des observations effectuées dans le monde réel. En mathématiques, nul besoin d'établir ce genre de procédure. Mais qu'est donc une démonstration ? Ce type de raisonnement consiste à partir de prémisses jugées « évidentes », ou déjà démontrées, et à user de la logique pour arriver à l'établissement d'une propriété donnée. Cette propriété peut alors servir de point de départ, de prémisse, pour une nouvelle démonstration…

Si l'on prend le chemin à l'envers, on remonte, dans le cadre d'une théorie donnée, le cheminement de toutes les démonstrations pour ne retenir que toutes les prémisses initiales. Le chemin étant fini, on en arrive inéluctablement à l'acceptation d'affirmations dont on ne peut fournir aucune preuve : les axiomes.

 
Des vérités évidentes ? Pas toujours !

Étymologiquement, le terme axiome vient du grec ancien αξιωμα, signifiant « digne d'être pris en considération et donc, évident en soi », qui dérive lui-même de l'adjectif αξιος, signifiant « digne ». Il désigne une vérité indémontrable qui doit être admise. Pour les philosophes grecs de l'Antiquité, l'axiome est une affirmation évidente, qui n'a nul besoin de preuve. En mathématiques, le terme « axiome » a continué à désigner jusqu'au début du XIX^e siècle une proposition évidente en elle-même, dans la plus pure tradition mathématique grecque des Éléments d'Euclide. Les questions essentielles que se sont posées les chercheurs en fondements mathématiques aux XIX^e et XX^e siècles ont bouleversé notre conception des mathématiques : de telles vérités auto-suffisantes existent-elles ? Sont-elles absolues ? Uniques ? Et surtout, que signifie l'« évidence » ?

De nos jours, un axiome désigne une vérité première, acceptée sans justification, à l'intérieur d'une théorie mathématique, et exclusivement dans ce cadre. L'ensemble des axiomes d'une théorie constitue ce que l'on appelle une axiomatique. Cette dernière doit être non contradictoire ; c'est là sa seule contrainte. Aucun mathématicien n'attribue plus aujourd'hui aux axiomes qu'il choisit une quelconque « valeur morale », ou une « valeur de vérité ». Ils demeurent à son libre choix sous l'unique contrainte de la cohérence interne. Il n'est plus question en mathématiques de comprendre le monde. Cette tâche échoit aux autres disciplines scientifiques ! En mathématiques, il est uniquement question de demeurer cohérent.

Dans le cadre axiomatique actuel, les axiomes ne ressemblent plus en rien aux vérités évidentes des premiers mathématiciens. Ils veulent échapper au cadre sémantique, qui ne peut que nuire à la généralité qu'ils veulent atteindre : ils se contentent de postuler l'existence d'objets et de relations entre ces objets. Les objets dont on suppose l'existence ne sont pas définis au sens usuel d'un dictionnaire. Certes, l'utilisation de termes courants pour les désigner peut être vue comme une aide à la représentation des concepts qu'ils recouvrent, mais ce choix engendre aussi une certaine forme de méta-compréhension ou même de sous-compréhension. On postule aussi l'existence de relations entre ces objets. Ce sont exclusivement ces hypothèses d'existence d'objets et de relations qui contiennent et définissent totalement leurs natures. Tout, en mathématiques, est donc construit à partir d'hypothèses d'existence d'objets (non définis) et d'hypothèses d'existence de relations (définies par l'hypothèse de leur existence) entre ces différents objets. Vient ensuite le raisonnement logique, basé généralement sur le principe du tiers exclus (les choses sont vraies ou fausses), qui autorise la démonstration de théorèmes.

Le raisonnement logique

Ainsi, dans le cadre des axiomatiques actuelles, les axiomes retenus en définitive manquent de sens intuitif. C'est particulièrement vrai en théorie des ensembles ! Or cette théorie est fondamentale : elle est à la base de la construction de tout l'immeuble mathématique, permettant notamment la construction des indispensables ensembles de nombres (voir le précédent dossier). L'axiomatique la plus couramment retenue en théorie des ensembles est celle qui fut proposée par les mathématiciens Ernst Zermelo et Abraham Fraenkel dans la première décennie du XX^e siècle, poursuivant les travaux initiés par Georg Cantor.

Cette axiomatique possède un énorme avantage : elle permet d'échapper aux paradoxes logiques, comme celui de Bertrand Russell, qui pigmentent toute théorie trop naïve des ensembles. De fait, nous devons admettre qu'il existe des collections d'objets parfaitement définies par une propriété partagée par chacun d'eux et… qui ne sont pas des ensembles au sens mathématique ! Il convient d'écarter certaines définitions « en compréhension non restreinte » pour éviter l'acceptation d'objets pathologiques, comme par exemple « l'ensemble de tout ce qui n'est pas un chat ».

L'axiomatique de Zermelo–Fraenkel (ZF en abrégé) peut être, ou non, complétée par l'axiome du choix : pour tout ensemble X d'ensembles non vides, il existe une fonction définie sur X, appelée fonction de choix, qui, à chaque ensemble A appartenant à X, associe un élément de cet ensemble A. Il fut formulé dès 1904 par  Zermelo pour la démonstration de son fameux théorème. Le mathématicien Bertrand Russell en donne selon son habitude une illustration amusante et originale (voir en encadré).

L'axiome du choix, de même que l'hypothèse du continu (selon laquelle il n'existe pas d'infini intermédiaire entre le dénombrable et le continu) sont indépendants de l'axiomatique ZF. Cette propriété fut démontrée par le mathématicien Paul Joseph Cohen en 1963, alors qu'il n'avait pas 30 ans, ce qui lui permit d'être distingué par une médaille Fields en 1966.

Une théorie bien concrète : le cerveau

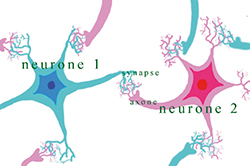
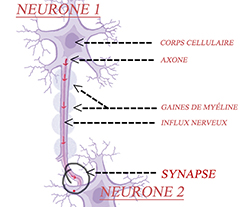
Il est impossible de parler d'intuition ou de mathématiques sans se pencher sur l'organe essentiel qui nous permet de ressentir l'une et de construire les autres. On s'attend donc à voir jouer par le fonctionnement de notre système cérébral un rôle primordial dans les différents processus mis en place. Notre cerveau est constitué de deux types d'objets : des cellules, les neurones, objets dont on ne donne pas de définition, et des connections intercellulaires, les synapses, qui concrétisent les relations existantes entre les différentes cellules. Voilà qui est extraordinaire : il possède donc très exactement la même structure que n'importe quelle axiomatique mathématique. Il y a identification totale entre toute théorie mathématique et un ensemble de réseaux neuronaux. Pas étonnant dès lors que notre cerveau soit une extraordinaire machine à créer des modèles, des représentations de fragments de réel ! Mais il y a plus : cette constatation est un argument décisif en faveur de la totale humanité des mathématiques. Ce qui ne va pas plaire à tous les mathématiciens…