Pourquoi l'utilisation d'un dictionnaire, aussi volumineux soit-il, est-elle aussi aisée ? Parce que tout y est bien rangé ! L'ordre alphabétique nous enlève une belle épine du pied. Il existe bien d'autres situations dans lesquelles nous sommes confrontés à un processus de classement. Les derniers Jeux olympiques donnent des exemples à la pelle.

Un peu d'ordre… 

Quels sont les caractères communs à toutes ces façons de classer ? Les mathématiciens ont dégagé trois notions clés qui permettent de définir une relation d'ordre R sur un ensemble E :

– R doit être réflexive, c'est-à-dire que, pour tout élément x de E, on a x R x ;

– R doit être transitive, c'est-à-dire que si x R y et y R z alors x R z ;

– enfin, R doit être antisymétrique, c'est-à-dire que si x est différent de y alors x R y ou bien y R x, mais pas les deux ! Dit autrement, si x R y et y R x alors x = y.

On retrouve bien ici, de manière formelle, toutes les propriétés de l'inégalité utilisée classiquement sur l'ensemble des nombres réels. En revanche, l'inégalité stricte n'est pas une relation d'ordre : elle n'est pas réflexive.

L'ordre lexicographique est aussi une relation d'ordre, tout comme l'inclusion. Mais si on peut toujours comparer deux nombres réels, si on peut toujours placer deux mots l'un par rapport à l'autre dans le dictionnaire, on ne peut pas toujours comparer deux ensembles par la relation d'inclusion ! Ainsi, les ensembles A = {0 ; 1} et B = {1 ; 2} sont bien inclus dans {0 ; 1 ; 2 ; 3}, mais A n'est pas inclus dans B, et B n'est pas inclus dans A. Ce phénomène se produit dans des situations de la vie courante. Imaginez un tournoi sportif opposant trente-deux athlètes. Chaque sportif en affronte un autre, les gagnants sont qualifiés pour l'étape suivante, et on recommence jusqu'en finale. Le premier est celui qui remporte la finale, le deuxième est son opposant malheureux, mais pour déterminer le troisième et les suivants, ça se corse. Compter le nombre de rencontres gagnées permet de comparer certains joueurs, mais pas tous ! Lorsque tous les éléments de E sont comparables avec R, on dit que E est totalement ordonné.

Certaines relations d'ordre présentent des particularités intéressantes. Pour un bon ordre, on exige que toute partie de E possède un plus petit élément. C'est le cas de l'inégalité sur l'ensemble des entiers naturels.

On peut parfois avoir envie de regrouper certains éléments d'un ensemble, d'identifier ceux qui jouent un rôle identique dans une structure. Pour cela, il suffit de construire une nouvelle relation binaire R, appelée relation d'équivalence. Comme pour une relation d'ordre, celle-ci doit être réflexive (un élément est identifié avec lui-même !) et transitive. En revanche, il faut cette fois-ci que R soit symétrique, c'est-à-dire que si x R y, alors y R x aussi.

Dans Science et Méthode (Flammarion, 1908), Henri Poincaré affirmait que « la mathématique est l'art de donner le même nom à des choses différentes ». C'est ce que permettent de faire les relations d'équivalence ! En effet, on peut maintenant regrouper ensemble tous les éléments d'un ensemble E qui sont en relation. Ces sous-ensembles, qu'on appelle les classes d'équivalence, sont par construction tous disjoints et tout élément de E appartient à une classe d'équivalence (éventuellement réduite à un seul élément). Cela forme une partition de l'ensemble E.

À partir d'un ensemble E et d'une relation R, ont peut construire un nouvel ensemble : celui des classes d'équivalences de E par R. Le fait de se donner une partition d'un ensemble E permet aussi de définir une relation d'équivalence sur E. L'ensemble des classes d'équivalence obtenu est appelé espace quotient, noté E / R. Ce point de vue est intéressant quand les propriétés « passent au quotient ». Prenons ainsi E = Z et considérons pour n ≥ 2 la relation d'équivalence consistant à associer les entiers qui ont le même reste dans la division euclidienne par n. Comme il y a n restes possibles (de 0 à n – 1), on obtient n classes d'équivalences. L'addition des entiers relatifs se transporte très bien aux classes d'équivalences, ce qui permet de faire des calculs « modulo n » dans les ensembles notés Z / nZ.

Moins par moins donne plus

De même, si on considère sur (R \ {0},  \( \times\) ) la relation d'équivalence consistant à associer les nombres de même signe, on obtient par passage au quotient la fameuse règle des signes ânonnée par les jeunes collégiens : « Moins par moins donne plus, moins par plus donne moins… »

Les ensembles quotients offrent un nouveau regard sur les objets géométriques. Considérons sur le plan \( \mathbb{R}^2\) la relation consistant à associer deux couples (x, y) et (x', y') si les différences x' – x et y' – y sont des entiers relatifs. Pour déterminer l'ensemble quotient, on peut se ramener dans un premier temps au carré [0, 1] \( \times\) [0, 1] ; il ne reste alors plus qu'à « recoller les bords ». On obtient alors un tore !

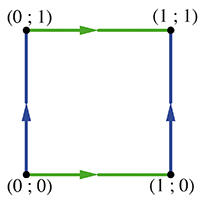
Ce procédé permet de créer de nouveaux espaces dans lesquels d'autres géométries que celle enseignée dans le secondaire sont possibles ! C'est ainsi que l'on peut construire les espaces projectifs. La recette est simple : il suffit de considérer l'ensemble des vecteurs non nuls de \( \mathbb{R}^n\) et la relation de colinéarité. Prenons le cas de la droite projective réelle. Elle est obtenue à partir de l'ensemble des vecteurs non nuls du plan. Deux vecteurs sont associés s'ils sont colinéaires. À quel objet correspond l'ensemble quotient obtenu ? Par colinéarité, on peut se contenter de regarder les vecteurs de norme 1, ce qui revient à considérer un cercle unitaire. Les points diamétralement opposés sont associés car ils correspondent à deux vecteurs colinéaires. Il ne nous reste donc plus qu'un demi-cercle dont les extrémités sont associées, ce qui donne… un cercle ! La droite projective réelle est un cercle. Le cas du plan projectif réel se traite de même (voir en encadré).